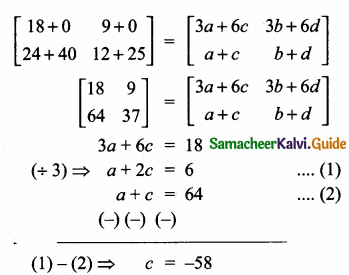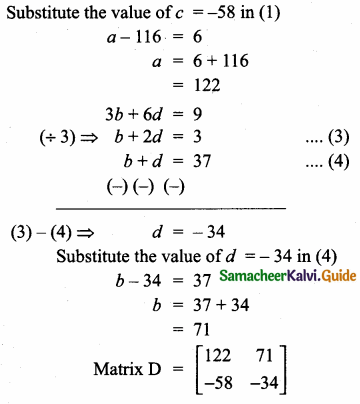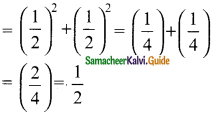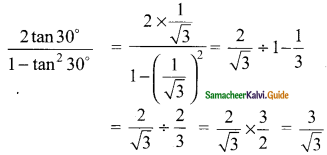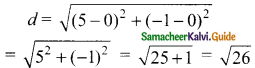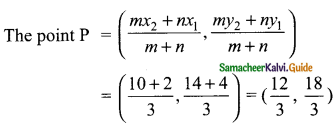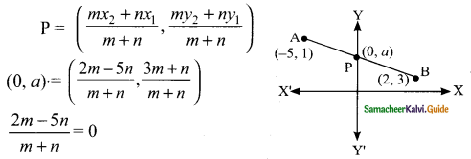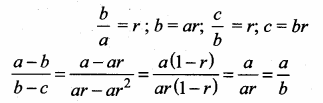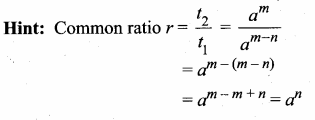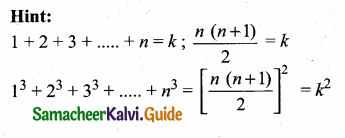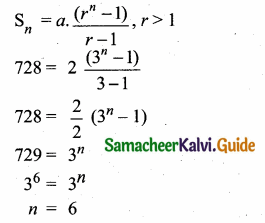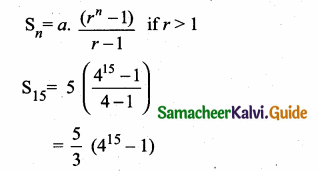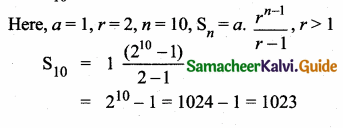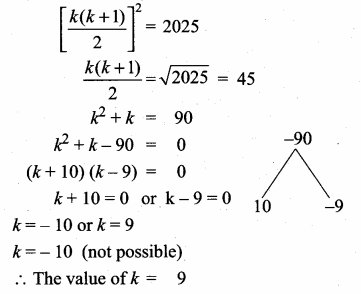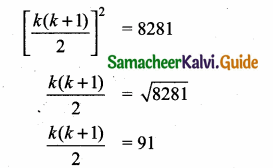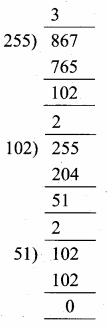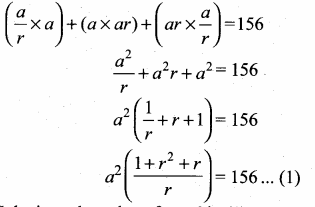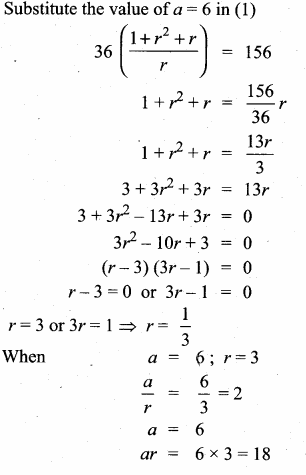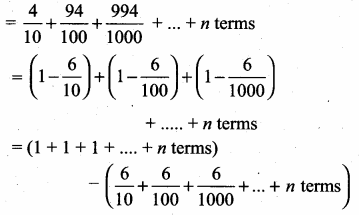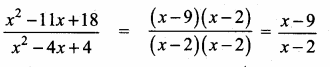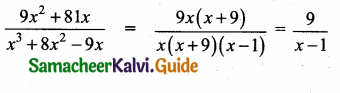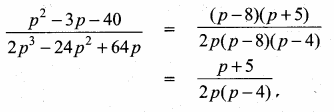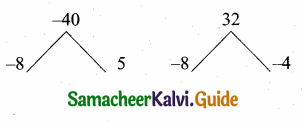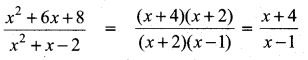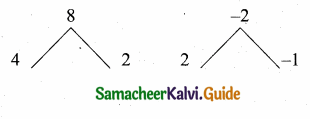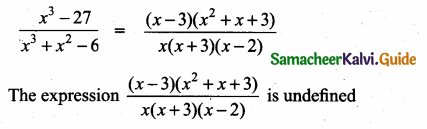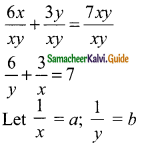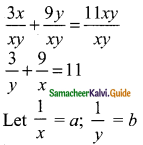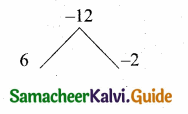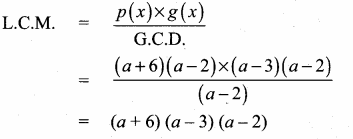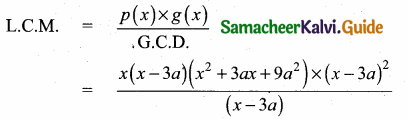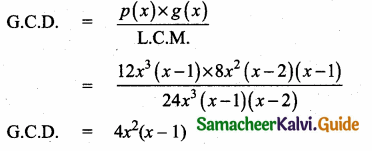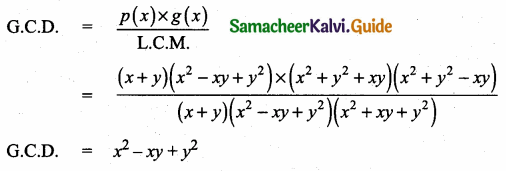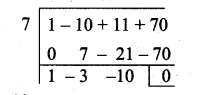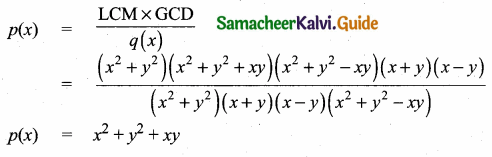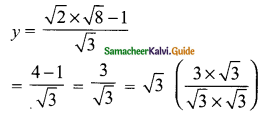Bhagya

Students can download Maths Chapter 3 Algebra Unit Exercise 3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Unit Exercise 3

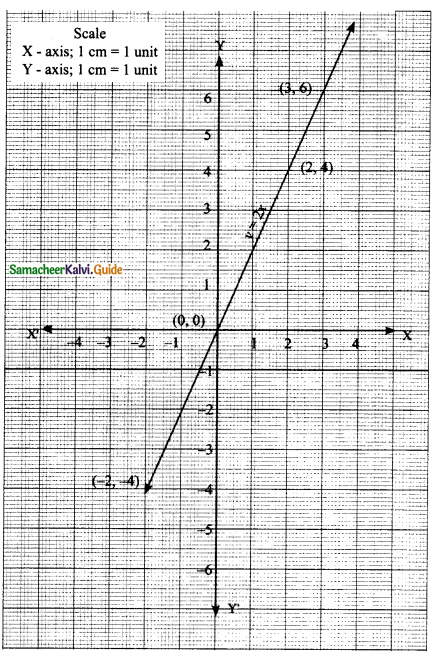
Question 1.
Solve
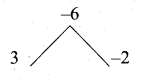
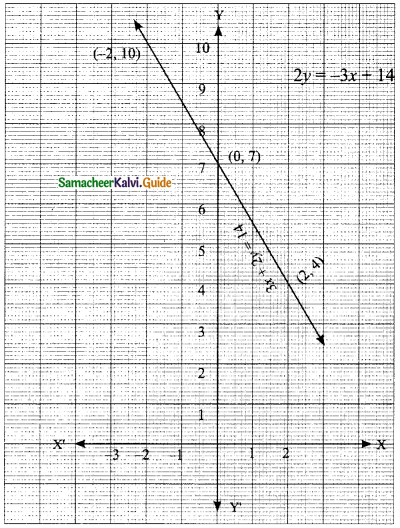
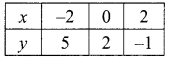
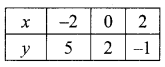
\(\frac { 1 }{ 3 } \) (x + y – 5) = y – z = 2x – 11 = 9 – (x + 2z)
Answer:
\(\frac { 1 }{ 3 } \) (x + y – 5) = y – z
x + y – 5 = 3y – 3z
x + y – 3y + 3z = 5
x – 2y + 3z = 5 ….(1)
y – z – 2x – 11
-2 x + y – z = -11
2x – y + z = 11 …..(2)
2x – 11 = 9-(x + 2 z)
2x – 11 = 9 – x – 2z
2x + x + 2z = 9 + 11
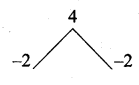
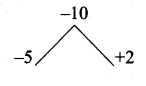
3x + 2z = 20 ….(3)

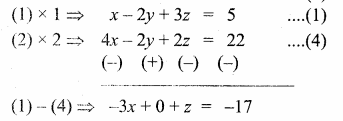
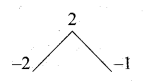
3x – z = 17 …. (5)


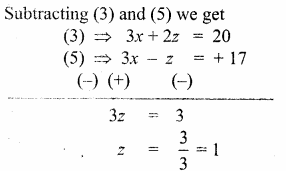
Substitute the value of z = 1 in (3)
3x + 2(1) = 20
3x = 20 – 2
3x = 18
x = \(\frac { 18 }{ 3 } \) = 6
substitute the value of x = 6, z = 1 in (2)
2(6) – y + 1 = 11
12 – y + 1 = 11
13 – y = 11
-y = 11 – 13
-y = -2
y = 2
∴ The value of x = 6, y = 2 and z = 1

Question 2.
One hundred and fifty students are admitted to a school. They are distrbuted over three sections A, B and C. If 6 students are shifted from section A to section C, the sections will have equal number of students. If 4 times of students of section C exceeds the number of students of section A by the number of students in section B, find the number of students in the three sections.
Answer:
Let the number of students in section A be “x”
Let the number of students in section B be “y”
Let the number of students in section C be “z”
By the given first condition
x + y + z = 150 ……(1)
again by the second condition
x – 6 = z + 6
x – z = 6 + 6
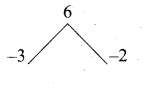
x – z = 12 ….(2)
again by the third condition
x + y = 4z
x + y – 4z = 0
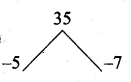
x + y – 4z = 0 ….(3)
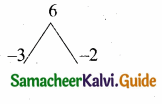
Subtracting (1) and (3)

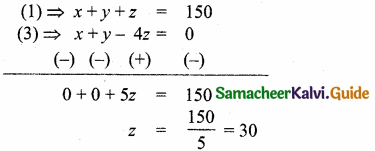
Substitute the value of z = 30 in (2)
x – 30 = 12
x = 12 + 30
= 42
Substitute the value of x = 42 and z = 30 in (1)
42 + y + 30 = 150
y + 72 = 150
y = 150 – 72
= 78
Number of students in section A, B and C are = 42, 78 and 30.

Question 3.
In a three-digit number, when the tens and the hundreds digit are interchanged the new number is 54 more than three times the original number. If 198 is added to the number, the digits are reversed. The tens digit exceeds the hundreds digit by twice as that of the tens digit exceeds the unit digit. Find the original number.
Answer:
Let the hundred digit be x
the tens digit be y and the unit digit be z
∴ The number is 100x + 10y + z
By the given first condition
100y + 10x + z = 54 + 3 (100x + 10y + z)
100y + 10x + z = 54 + 300x + 30y + 3z
-290x + 70y – 2z = 54 (÷ -2)
145x-35y + z = -27 ….(1)
Again by the second condition
198 + 100x + 10y + z = 100z + 10y + x
99x – 99z = -198 (÷ 99)
x – z = -2 ….(2)
Again by the third condition
y – x = 2(y – z)
y – x = 2y – 2z
– x – y + 2z = 0
x + y – 2z = 0 ….(3)

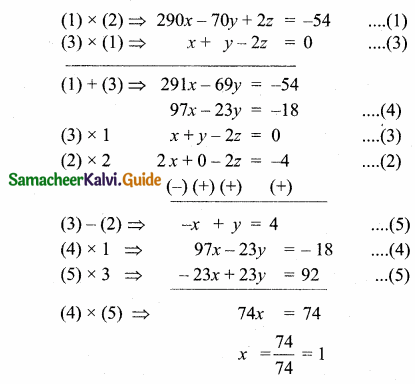
substitute the value of x = 1 in …….(2)
1 – z = -2
3 = z
∴ z = 3
substitute the value of x = 1 and z = 3 in …….(3)
1 – y – 6 = 0
y – 5 = 0
y = 5
∴ The number is 153

Question 4.
Find the least common multiple of xy(k² +1) + k(x² + y²) and xy(k² – 1) + k(x² – y²).
Solution:
xy (k² + 1) + k (x² + y²) …………… (1)
xy(k² – 1) + k(x² – y²) …………… (2)
(1) ⇒ xyk² + xy + kx² + ky²
(2) ⇒ xyk² – xy + kx² – ky²
(1) ⇒ yk (xk + y) + x (xk + y)
= (xk + y) (x + yk)
(2) ⇒ yk (xk – y) + x (xk – y)
= (x + yk) (xk – y)
∴ L.C.M. : (x + yk) (xk + y) (xk – y)
= (x + yk) (x²k² – y²)

Question 5.
Find the GCD of the following by division algorithm
2x⁴ + 13x³ + 27x² + 23x + 7,
x³ + 3x² + 3x + 1, x² + 2x + 1
Answer:
p(x) = 2x⁴ + 13x³ + 27x² + 23x + 7
g(x) = x³ + 3x² + 3x + 1
r(x) = x² + 2x + 1
(i) Find the G.C.D. of p(x) and g(x)

(ii) Find the G.C.D. of r(x) and the G.C.D. of p(x) and g(x)

∴ G.C.D.= x² + 2x + 1
∴ G.C.D. of the three
polynomials = x² + 2x + 1

Question 6.
Reduce the given Rational expressions to its lowest form
(i) \(\frac{x^{3 a}-8}{x^{2 a}+2 x^{a}+4}\)
Answer:
x^3a – 8 = (x^a)³ – 2³
(using the formula a³ – b³ = (a – b)(a² + ab + b²)
= (x^a – 2)[(x^a)² + x^a × 2 + 2²]
= (x^a – 2) (x^2a + 2x^a + 4)

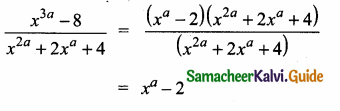
(ii) \(\frac{10 x^{3}-25 x^{2}+4 x-10}{-4-10 x^{2}}\)
Answer:
10x³ – 25x² + 4x – 10 = 5x²(2x – 5) + 2 (2x – 5)
= (2x – 5) (5x² + 2)
– 4 – 10x² = -2 (2 + 5x²)
= -2(5x² + 2)

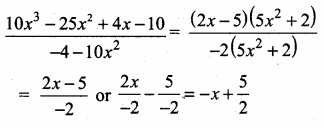
Question 7.
Simplify

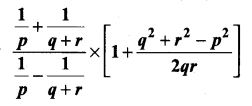
Answer:

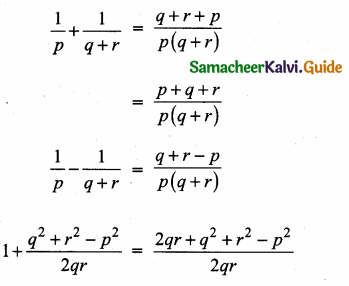
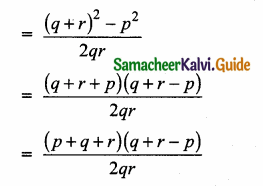
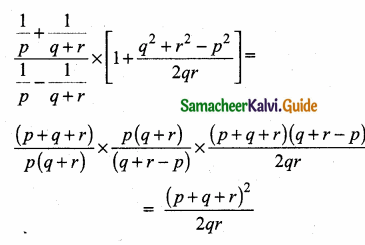
Question 8.
Arul, Ravi and Ram working together can clean a store in 6 hours. Working alone, Ravi takes twice as long to clean the store as Arul does. Ram needs three times as long as Arul does. How long would it take each if they are working alone?
Answer:
Let the time taken by Arul be “x” hours
Let the time taken by Ravi be “y” hours
Let the time taken by Ram be “z” hours
By the given first condition
\(\frac { 1 }{ x } \) + \(\frac { 1 }{ y } \) + \(\frac { 1 }{ z } \) = \(\frac { 1 }{ 6 } \)
Again by the given second condition
\(\frac { 1 }{ x } \) = 2 × \(\frac { 1 }{ y } \)
\(\frac { 1 }{ x } \) – \(\frac { 2 }{ y } \) = 0
By the given third condition
3 × \(\frac { 1 }{ z } \) = \(\frac { 1 }{ x } \)
– \(\frac { 1 }{ x } \) + \(\frac { 3 }{ z } \) = 0
Let \(\frac { 1 }{ x } \) = a, \(\frac { 1 }{ y } \) = b, \(\frac { 1 }{ z } \) = c
a + b + c = \(\frac { 1 }{ 6 } \)
6a + 6b + 6c = 1 …….(1)
a – 2b = 0 ……….(2)
-a + 3c = 0 …………(3)

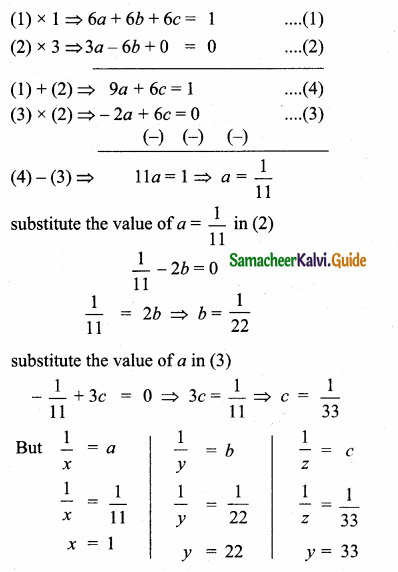
Arul take 11 hours, Ravi take 22 hours and Ram takes 33 hours.

Question 9.
Find the square root of 289x⁴ – 612x³ + 970x² – 684x + 361.
Answer:

Question 10.
Solve \(\sqrt { y+1 }\) + \(\sqrt { 2y-5 }\) = 3
Answer:
\(\sqrt { y+1 }\) + \(\sqrt { 2y-5 }\) = 3
(squaring on bothsides)

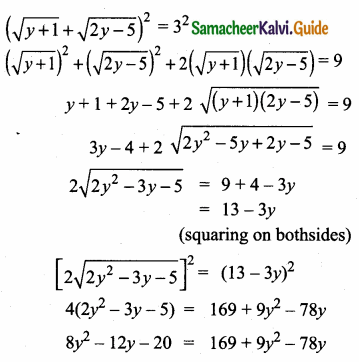
8y² – 9y² – 12y + 78y – 20 – 169 = 0
-y² – 66y – 189 = 0
y² – 66y + 189 = 0
(y – 3) (y – 63) = 0

y – 3 or y = 63
The value of y is 3 and 63

Question 11.
A boat takes 1.6 hours longer to go 36 kins up a river than down the river. If the speed of the water current is 4 km per hr, what is the speed of the boat in still water?
Answer:
Let the speed of the boat in still water be “x”
Time taken to go for up of a river = \(\frac { 36 }{ x+4 } \)
By the given condition
\(\frac { 36 }{ x-4 } \) – \(\frac { 36 }{ x+4 } \) = 1.6

The speed of the boat in still water = 14 km/hr

Question 12.
Is it possible to design a rectangular park of perimeter 320 m and area 4800 m2? If so find its length and breadth.
Answer:
Let the length of the rectangular park be “l”
and the breadth of the rectangular park be “b”
Perimeter of the park = 320 m
2 (l + b) = 320
l + b = 160
l = 160 – b ……….(1)
Area of the park = 4800 m²
l × b = 4800 ….(2)
substitute the value of l = 160 – b in (2)
(160 – b)b = 4800
160b – b² = 4800
b² – 160b + 4800 = 0
(b – 120) (b – 40) = 0

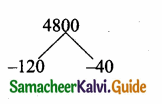
b = -120 = 0 or b – 40 = 0
b = 120 or b = 40
If breadth is 120 length is 40
If breadth is 40 length is 120
Length of the park = 120 m
Breadth of the park = 40 m

Question 13.
At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than \(\frac{t^{2}}{4}\) Find t.
Answer:
Time needed by the minutes hand to show
3 pm = (60 – 1) minutes
By the given condition


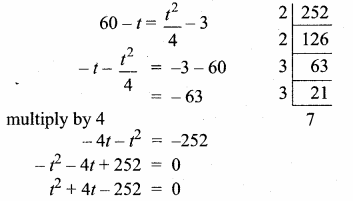
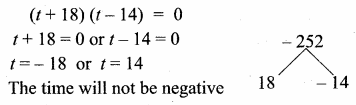
∴ The value of t = 14 minutes

Question 14.
The number of seats in a row is equal to the total number of rows in a hall. The total number of seats in the hall will increase by 375 if the number of rows is doubled and the number of seats in each row is reduced by 5. Find the number of rows in the hall at the beginning.
Answer:
Let the number of rows in the hall be “x”
∴ Total number of rows = x
Total number of seats in the hall is “x2”
By the given condition
x² + 375 = 2x (x – 5)
x² + 375 = 2x²– 10x
x² – 2x² + 10x + 375 = 0
– x² + 10x + 375 = 0
– x² – 10x – 375 = 0
(x – 25) (x + 15)
x – 25 = 0 or x + 15 = 0
x = 25 or x = – 15

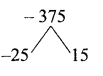
Number of rows in the hall = 25

Question 15.
If α and β are the roots of the polynomial f(x) – x² – 2x + 3, find the polynomial whose roots are
(i) α + 2, β + 2
Answer:
α and β are the roots of the polynomial
x² – 2x + 3 = 0
α + β = 2; αβ = 3
(i) Sum of the roots = α + 2 + β + 2
= α + β + 4
= 2 + 4
= 6
Product of the roots = (α + 2) (β + 2)
= αβ + 2α + 2β + 4
= αβ + 2(α + β) + 4
= 3 + 4 + 4
= 11
The quadratic polynomial
x² – (sum of the roots) x + product of the roots = 0
x² – (6) x + 11 = 0
x² – 6x + 11 = 0

(ii) \(\frac{\alpha-1}{\alpha+1}, \frac{\beta-1}{\beta+1}\)
Answer:
Sum of the roots


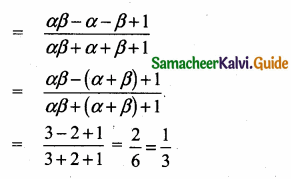
The quadratic polynomial is
x² – (sum of the roots) + products of the roots = 0
x² – (\(\frac { 2 }{ 3 } \)) x + \(\frac { 1 }{ 3 } \) = 0
3x² – 2x + 1 = 0

Question 16.
If -4 is a root of the equation x² + px – 4 = 0 and if the equation x² + px + q = 0 has equal roots, find the values of p and q.
Solution:
f(x) = x² + px – 4 = 0
If -4 is a root, then
f(-4) = (-4)² + P(-4) – 4 = 16 – 4p – 4 = 0
12 – 4p = 0
-4p = -12
p = 3
x² + 3x + q =0 has equal roots,
∆ = b² – 4ac = 0
3² – 4 × 1 × q = 0
9 – 4q = 0
-4 q = -9
q = \(\frac{9}{4}\)
p = 3, q = \(\frac{9}{4}\)

Question 17.
Two farmers Senthil and Ravi cultivates three varieties of grains namely rice, wheat and ragi. If the sale (in ₹) of three varieties of grains by both the farmers in the month of April is given by the matrix.

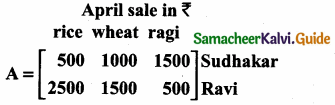
and the May month sale (in ₹) is exactly twice as that of the April month sale for each variety.
(i) What is the average sales of the months April and May.
Answer:
(i) Let A represent the sale on April

Let B represent the sale on May

Average sale of the month April and May

(ii) If the sales continue to increase in the same way in the successive months, what will be sales in the month of August?
Answer:
If it increasing in the successive months of
May sale is 2 (April sale)
June sale is 4 (April sale)
July sale is 8 (April sale)
August sale is 16 (April sale)
Sales in the month of August

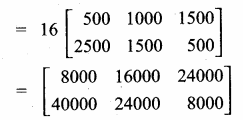
Question 18.
If cos = I₂, find x.
Answer:

Question 19.
Given

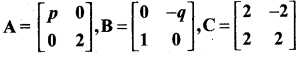
and if BA = C², find p and q
Answer:

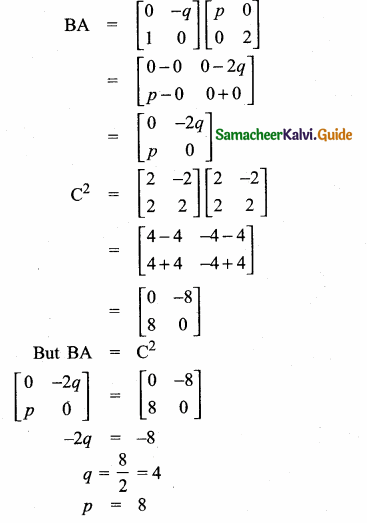
∴The value of p = 8 and q = 4

Question 20.

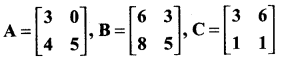
find the matrix D, such that CD – AB = 0
Answer:
Given

Students can download Maths Chapter 6 Trigonometry Ex 6.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.5

Question 1.
If sin 30° = x and cos 60° = y, then x² + y² is …….
(a) \(\frac{1}{2}\)
(b) 0
(c) sin 90°
(d) cos 90°
Solution:
(a) \(\frac{1}{2}\)
Hint:
sin 30° = x = \(\frac{1}{2}\)
cos 60° = y = \(\frac{1}{2}\)
x² + y²

Question 2.
If tan θ = cot 37°, then the value of θ is ………
(a) 37°
(b) 53°
(c) 90°
(d) 1°
Solution:
(b) 53°
Hint:
tan θ = cot 37°
= cot (90° – 53°)
= tan 53°
The value of θ is 53°

Question 3.
The value of tan 72°. tan 18° is ………
(a) 0
(b) 1
(c) 18°
(d) 72°
Solution:
(b) 1
Hint:
tan 72° . tan 18° = tan 72° . tan (90° – 72°)
= tan 72° . cot 72°
= tan 72° × \(\frac{1}{tan 72°}\)
= 1

Question 4.
The value of \(\frac{2 tan 30°}{1 – tan^{2} 30°}\) is equal to ………
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Solution:
(c) tan 60°
Hint:

= √3 = tan 60°

Question 5.
If 2 sin 2θ = √3 then the value of θ is ………
(a) 90°
(b) 30°
(c) 45°
(d) 60°
Solution:
(b) 30°
Hint:
2 sin 2θ = √3 ⇒ sin 2θ = \(\frac{√3}{2}\)
sin 2θ = sin 60° ⇒ 2θ = 60°
θ = 30°

Question 6.
The value of 3 sin 70° sec 20° + 2 sin 39° sec 51° is ………
(a) 2
(b) 3
(c) 5
(d) 6
Solution:
(c) 5
Hint:
3 sin 70° sec 20° + 2 sin 39° sec 51°
= 3. sin 70° . sec (90° – 70°) + 2 sin 39° . sec (90° – 39°)
= 3. sin 70° . cosec 70° + 2 sin 39° . cosec 39°
= 3. sin70° × \(\frac{1}{sin 70°}\) + 2 sin 39° × \(\frac{1}{sin 39°}\)
= 3 + 2
= 5

Question 7.
The value of \(\frac{1-tan^{2}45°}{1+tan^{2}45°}\) is ……..
(a) 2
(b) 1
(c) 0
(d) \(\frac{1}{2}\)
Solution:
(c) 0
Hint:
\(\frac{1-tan^{2}45°}{1+tan^{2}45°}\) = \(\frac{1-1}{1+1}\)
= \(\frac{0}{2}\) = 0

Question 8.
The value of cosec (70° + θ) – sec (20° + θ) + tan (65° + θ) – cot (25° + θ) is ……..
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:
cosec (70° + θ) – sec (20° – θ) + tan (65° + θ) – cot (25° – θ)
= sec [90° – (70° + θ)] – sec (20° – θ) + tan (65° + θ) – tan [90° – (25° – θ)]
= sec (20° – θ) – sec (20° – θ) + tan (65° + θ) – tan (65° + θ)
= 0

Question 9.
The value of tan 1° . tan 2° . tan 3°…. tan 89° is ………
(a) 0
(b) 1
(c) 2
(d) \(\frac{√3}{2}\)
Solution:
(b) 1
Hint:
tan 1° . tan 2° . tan 3° …….. tan 89°
= tan (90° – 89°). tan (90° – 88°) .tan (90° – 87°) …….. tan 45° . tan (89°)
= cot 89° . cot 88°. cot 87°. ……. tan 45° …….. tan 87°. tan 88°. tan 89°
= 1

Question 10.
Given that sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\), then the value of α + β is ………
(a) 0°
(b) 90°
(c) 30°
(d) 60°
Solution:
Hint:
sin α = \(\frac{1}{2}\)
sin 30° = \(\frac{1}{2}\) ∴ α = 30°
cos β = \(\frac{1}{2}\) ∴ β = 60°
∴ α + β = 30° + 60°
= 90°

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.6

Question 1.
If the y-coordinate of a point is zero, then the point always lies ……..
(a) in the I quadrant
(b) in the II quadrant
(c) on x-axis
(d) on y-axis
Solution:
(c) on x-axis

Question 2.
The points (-5, 2) and (2, -5) lie in the ……….
(a) same quadrant
(b) II and III quadrant respectively
(c) II and IV quadrant respectively
(d) IV and II quadrant respectively
Solution:
(c) II and IV quadrant respectively

Question 3.
On plotting the points O (0, 0), A (3, -4), B (3, 4) and C (0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?
(a) Square
(b) Rectangle
(c) Trapezium
(d) Rhombus
Solution:
(c) Trapezium

Question 4.
If P (-1, 1), Q ( 3, -4), R (1, -1), S (-2, -3) and T (- 4, 4) are plotted on a graph paper, then the points in the fourth quadrant are ………
(a) P and T
(b) Q and R
(c) only S
(d) P and Q
Solution:
(b) Q and R

Question 5.
The point whose ordinate is 4 and which lies on the v-axis is ……….
(a) (4, 0)
(b) (0, 4)
(c) (1, 4)
(d) (4, 2)
Solution:
(b) (0, 4)

Question 6.
The distance between the two points (2, 3) and (1, 4) is ……..
(a) 2
(b) \(\sqrt{56}\)
(c) \(\sqrt{10}\)
(d) √2
Solution:
(d) √2
Hint:
\(\sqrt{(1-2)^{2}+(4+3)^{2}}\)
= \(\sqrt{(-1)^{2}+1^{2}}\)
= \(\sqrt{1+1}\)
= √2

Question 7.
If the points A (2, 0), B (-6, 0), C (3, a – 3) lie on the x-axis then the value of a is ……..
(a) 0
(b) 2
(c) 3
(d) -6
Solution:
(c) 3
Hint:
a – 3 = 0 ⇒ a = 3

Question 8.
If (x + 2, 4) = (5, y – 2), then the coordinates (x, y) are ………
(a) (7, 12)
(b) (6, 3)
(c) (3, 6)
(d) (2, 1)
Solution:
(c) (3, 6)
Hint:
x + 2 = 5
∴ x = 5 – 2 = 3
and
4 = y – 2
4 + 2 = y
∴ y = 6

Question 9.
If Q₁, Q₂, Q₃, Q₄ are the quadrants in a Cartesian plane then Q₂ ∩ Q₃ is ……..
(a) Q₁ U Q₂
(b) Q₂ U Q₃
(C) Null set
(d) Negative x-axis
Solution:
(c) Null set

Question 10.
The distance between the point (5, -1 ) and the origin is ………
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(c) \(\sqrt{26}\)
Hint:

Question 11.
The coordinates of the point C dividing the line segment joining the points P (2, 4) and Q (5, 7) internally in the ratio 2 : 1 is ……..
(a) (\(\frac{7}{2}, \frac{11}{2}\))
(b) (3, 5)
(c) (4, 4)
(d) (4, 6)
Solution:
(d) (4, 6)
Hint:
A line divides internally in the ratio m : n
m = 2, n = 1
x₁ = 2, x₂ = 5
y₁ = 4, y₂ = 7

= (4, 6)

Question 12.
If p (\(\frac{a}{3}, \frac{b}{2}\)) is the mid-point of the line segment joining A (-4, 3) and B (-2, 4) then (a, b) is ………
(a) (-9, 7)
(b) (-3, \(\frac{7}{2}\))
(c) (9, -7)
(d) (3, –\(\frac{7}{2}\))
Solution:
(a) (-9, 7)
Hint:
Mid point of a line

\(\frac{a}{3}\) = -3 ⇒ a = -9
\(\frac{b}{2}\) = \(\frac{7}{2}\) ⇒ b = 7
(a, b) is (-9, 7)

Question 13.
In what ratio does the point Q (1, 6) divide the line segment joining the points P (2, 7) and R(-2, 3) ………
(a) 1 : 2
(6) 2 : 1
(c) 1 : 3
(d) 3 : 1
Solution:
(c) 1 : 3
Hint:
A line divides internally in the ratio m : n the point P =
(\(\frac{mx_{2}+nx_{1}}{m+n}\), \(\frac{my_{2}+ny_{1}}{m+n}\))

(1, 6) = (\(\frac{-2m+2n}{m+n}\), \(\frac{3m+7n}{m+n}\))
\(\frac{-2m+2n}{m+n}\) = 1
-2m + 2n = m + nx
-3m = n – 2n
3m = n
\(\frac{m}{n}\) = \(\frac{1}{3}\)
∴ m : n = 1 : 3
and
\(\frac{3m+7n}{m+n}\) = 6
3m + 7n = 6m + 6n
6m – 3n = 7n – 6n
3m = n
\(\frac{m}{n}\) = \(\frac{1}{3}\)

Question 14.
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (-3, 2), then the coordinate of the other end of the diameter is ……..
(a) (0, -3)
(b) (0, 9)
(c) (3, 0)
(d) (-9, 0)
Solution:
(d) (-9, 0)
Hint:
Let the other end of the diameter be (a, b)

Mid point of a line =
(\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(-3, 2) = \(\frac{3+a}{2}, \frac{4+b}{2}\)
\(\frac{3+a}{2}\) = -3
3 + a = -6
a = -6 – 3 = -9
and
\(\frac{4+b}{2}\) = 2
4 + b = 4
b = 4 – 4 = 0
The other end is (-9, 0)

Question 15.
The ratio in which the x-axis divides the line segment joining the points A (a₁, b₁) and B (a₂, b₂) is ……..
(a) b₁ : b₂
(b) -b₁ : b₂
(c) a₁ : a₂
(d) -a₁ : a₂
Solution:
(b) -b₁ : b₂
Hint:
A line divides internally in the ratio m : n the point P is,
(\(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}\))

The point P is (a, 0) = (\(\frac{ma_{2}+na_{1}}{m+n}, \frac{mb_{2}+nb_{1}}{m+n}\))
∴ \(\frac{mb_{2}+nb_{1}}{m+n}\) = 0
mb₂ + nb₁ = 0 ⇒ mb₂ = -nb₁
\(\frac{m}{n}\) = \(\frac{b_{1}}{b_{2}}\)
∴ m : n = -b₁ : b₂

Question 16.
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, -7) is ………
(a) 2 : 3
(b) 3 : 4
(c) 4 : 7
(d) 4 : 3
Solution:
(c) 4 : 7
Hint:
A line divides internally in the ratio m : n the point P

-7m + 4n = 0
4n = 7m
\(\frac{m}{n}\) = \(\frac{4}{7}\)
The ratio is 4 : 7

Question 17.
If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, -3) respectively, then the vertices A and B of the triangle are ……….
(a) (3, 2), (2, 4)
(b) (4, 0), (2, 8)
(c) (3, 4), (2, 0)
(d) (4, 3), (2, 4)
Solution:
(b) (4, 0), (2, 8)
Hint:

x₁ + x₂ = 6 → (1)
y₁ + y₂ = 8 → (2)
x₂ + x₃ = 2 → (3)
y₂ + y₃ = 2 → (4)
x₁ + x₃ = 4 → (5)
y₁ + y₃ = -6 → (6)
Adding (1) + (3) + (5) we get,
2(x₁ + x₂ + x₃) = 3
x₁ + x₂ + x₃ = 6
x₁ + x₃ = 4
∴ x₂ = 6 – 4 = 2
x₂ + x₃ = 2
x₁ = 6 – 2 = 4
Adding (2) + (4) + (6) we get,
2 (y₁ + y₂ + y₃) = 4
y₁ + y₂ + y₃ = 2
y₂ + y₃ = 2
∴ y₁ = 2 – 2 = 0
y₁ + y₃ = -6
y₂ = 2 + 6 = 8
∴ The vertices A is (4, 0) and B is (2, 8).

Question 18.
The mid-point of the line joining (-a, 2b) and (-3a, -4b) is ……..
(a) (2a, 3b)
(b) (-2a, -b)
(c) (2a, b)
(d) (-2a, -3b)
Solution:
(b) (-2a, -b)
Mid points of line

= (-2a, -b)

Question 19.
In what ratio does the y-axis divides the line joining the points (-5, 1) and (2, 3) internally ………
(a) 1 : 3
(b) 2 : 5
(c) 3 : 1
(d) 5 : 2
Solution:
(d) 5 : 2
Hint:
When it cut the y-axis the point P is (0, a)
A line divides internally in the ratio m : n the point

2m – 5n = 0 ⇒ 2m = 5n
\(\frac{m}{n}\) = \(\frac{5}{2}\) ⇒ m : n = 5 : 2

Question 20.
If (1, -2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is ………
(a) 6
(b) 5
(c) 4
(d) 3
Solution:
(b) 5
Hint:
Since ABCD is a parallelogram

Mid-point of AC = Mid-point of BD

\(\frac{1+x}{2}\) = \(\frac{6}{2}\) ⇒ 1 + x = 6 ⇒ x = 6 – 1 = 5
The value of x = 5

Students can download Maths Chapter 6 Trigonometry Ex 6.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.4

Question 1.
Find the value of the following:
(i) sin 49°
(ii) cos 74° 39′
(iii) tan 54° 26′
(iv) sin 21° 21′
(v) cos 33° 53′
(vi) tan 70° 17′
Solution:
(i) sin 49° = 0.7547

(ii) cos 74° 39′ = cos 74° 39′ + 3′
From the table we get,
cos 74° 36′ = 0.2656
Mean difference of 3 = 8
cos 74° 39′ = 0.2656 – 8
= 0.2648

(iii) tan 54° 26′ = tan 54° 24′
tan 54° 24′ = 1.3968
Mean difference of 2 = 17
tan 54° 26’ = 1.3968 + 17
= 1.3985

(iv) sin 21° 21′ = sin 21° 18’+ 3’
sin 21° 18’ = 0.3633
Mean difference of 3 = 8(+)
sin 21° 21′ = 0.3633 + 8
= 0.3641

(v) cos 33° 53′ = cos 33° 48’ + 5′
cos 33° 48′ = 0.8310
Mean difference of 5 = 8
cos 33° 53′ = 0.8310 – 8
= 0.8302

(vi) tan 70° 17′ = tan 70° 12’+ 5’
tan 70° 12′ = 2. 7776
Mean difference of 5 = 131
tan 70° 17′ = 2. 7776 + 131
= 2.7907

Question 2.
Find the value of θ if
(i) sin θ = 0.9975
(ii) cos θ = 0.6763
(iii) tan θ = 0.0720
(iv) cos θ = 0.0410
(v) tan θ = 7.5958
Solution:
(i) sin θ = 0.9975
From the table we get,
= 0.9974 + 0.0001
= 85° 54′ + 1′
= 85° 55′ (or) 85° 56′ (or) 85° 57

(ii) cos θ = 0.6763
= 0. 6769 – 0.0006′
= 47° 24′ + 3′
= 47° 27

(iii) tan θ = 0. 0720
= 0. 0717 + 0.0003
= 4° 6′ + 1′
= 4° 7′

(iv) cos θ = 0.0410
= 0.0419 – 0.0009
= 87° 36′ + 3′
= 87° 39′

(v) tan θ = 7. 5958
= 7. 5958 + 0 (from the natural table)
= 82° 30′ (tangent table)

Question 3.
Find the value of the following:
(i) sin 65° 39′ + cos 24° 57’ + tan 10° 10′
(ii) tan 70° 58′ + cos 15° 26′ – sin 84° 59′
Solution:
(i) sin 65° 39′ = 0.9111
cos 24° 57′ = 0.9066
tan 10° 10′ = 0.1793
sin 65° 39′ + cos 24° 57′ + tan 10° 10′
= 0.9111 + 0.9066 + 0.1793
= 1.9970
sin 65° 39′ + cos 24° 57′ + tan 10° 10′ = 1.9970

(ii) tan 70° 58′ = 2. 8982
cos 15° 26′ = 0. 9639
sin 84° 59′ = 0.9962
tan 70° 58′ + cos 15° 26′ – sin 84° 59′
= 2. 8982 + 0. 9639 – 0.9962
= 3.8621 – 0.9962
= 2.8659

Question 4.
Find the area of a right triangle whose hypotenuse is 10 cm and one of the acute angle is 24°24′.
Solution:
In the ΔABC,

sin 24° 24′ = \(\frac{AB}{AC}\)
0. 4131 = \(\frac{AB}{10}\)
∴ AB = 4.131 cm
In the ΔABC,
cos 24° 24′ = \(\frac{BC}{AC}\)
0.9107 = \(\frac{BC}{10}\)
∴ BC = 9.107 cm
Area of the right angle = \(\frac{1}{2}\) × BC × AB
= \(\frac{1}{2}\) × 9.107 × 4.131
= \(\frac{37.62}{2}\)
Area of the triangle = 18.81 cm²

Question 5.
Find the angle made by a ladder of length 5m with the ground, if one of its end is 4m away from the wall and the other end is on the wall.
Solution:
AC is the length of the ladder.

In the right ΔABC,
cos θ = \(\frac{BC}{AC}\)
cos θ = \(\frac{4}{5}\)
= 0.8
cos θ = 0.8000
θ = 36° 52′
Angle made by a ladder with the ground is 36° 52′

Question 6.
In the given figure, HT shows the height of a tree standing vertically. From a point P, the angle of elevation of the top of the tree (that is ∠P) measures 42° and the distance to the tree is 60 metres. Find the height of the tree.
Solution:
Let the height of the tree HT be “x”

In the ΔHTP,
tan 42° = \(\frac{HT}{PT}\)
0.9004 = \(\frac{x}{60}\)
x = 0.9004 × 60
= 54.024
The height of the tree = 54.02 m

Students can download Maths Chapter 2 Numbers and Sequences Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Additional Questions

I. Choose the correct answer.

Question 1.
The sum of the exponents of the prime factors in the prime factorisation of 504 is ……….
(1) 3
(2) 2
(3) 1
(4) 6
Answer:
(4) 6

Hint: 504 = 2³ × 3² × 7¹
Sum of the exponents
= 3 + 2 + 1 = 6

Question 2.
If two positive integers a and 6 are expressible in the form a = pq² and b = p³q ; p, q being prime numbers, then L.C.M. of (a, b) is ……………
(i) pq
(2) P² q²
(3) p³ q³
(4) P³ q²
Answer:
(4) P³ q²
Hint: a = p × q² and b = p³ × q
∴ L.C.M. of (a, b) is p³ q²

Question 3.
If n is a natural number then 7³ⁿ – 4³ⁿ is always divisible by …………….
(1) 11
(2) 3
(3) 33
(4) both 11 and 3
Answer:
(4) both 11 and 3
Hint: 7³ⁿ – 4³ⁿ is of the form a²ⁿ – b²ⁿ which is divisible by both a – b and a + b. So 7³ⁿ – 4³ⁿ is divisible by both 7 – 4 = 3 and 7 + 4 = 11.

Question 4.
The value of x when 200 = x (mod 7) is …………………
(1) 3
(2) 4
(3) 54
(4) 12
Answer:
(2) 4
Hint:

200 ≡ x (mod 7)
200 ≡ 4 (mod 7)
The value of x = 4

Question 5.
The common difference of the A.P.
\(\frac { -2 }{ 2b } \) , \(\frac { 1-6b }{ 2b } \), \(\frac { 1-12b }{ 2b } \) is …………….
(1) 2b
(2) -2b
(3) 3
(4) -3
Answer:
(4) -3
Hint:
\(\frac { 1-12b }{ 2b } \) – \(\frac { 1-6b }{ 2b } \) = \(\frac { 1-12b-1+6b }{ 2b } \) = \(\frac { -6b2 }{ 2b } \) = \(\frac { -6b }{ 2b } \) = -3

Question 6.
Which one of the following is not true?
(1) A sequence is a real valued function defined on N.
(2) Every function represents a sequence.
(3) A sequence may have infinitely many terms.
(4) A sequence may have a finite number of terms.
Answer:
(2) Every function represents a sequence.
Hint: A sequence is a function whose domain is the set of natural numbers.

Question 7.
The 8^th term of the sequence 1,1,2,3,5,8, ………. is ……….
(1) 25
(2) 24
(3) 23
(4) 21
Answer:
(4) 21
Hint: In fibonacci sequence
F_n = F_n-1 + F_n-2
F₈ = F₇ + F₆
8^th term = 6^th term + 7^th term
= 8 + (5 + 8) = 21

Question 8.
The next term of \(\frac { 1 }{ 20 } \) in the sequence \(\frac { 1 }{ 2 } \),\(\frac { 1 }{ 6 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 20 } \) is ……………
(1) \(\frac { 1 }{ 24 } \)
(2) \(\frac { 1 }{ 22 } \)
(3) \(\frac { 1 }{ 30 } \)
(4) \(\frac { 1 }{ 18 } \)
Answer:
(3) \(\frac { 1 }{ 30 } \)
Hint:
The general term t_n = \(\frac{1}{n(n+1)}\)
⇒ t₅ = \(\frac{1}{5(6)}\) = \(\frac { 1 }{ 30 } \)

Question 9.
If a, 6, c, l, m are in A.P, then the value of a – 46 + 6c – 4l + m is …………
(1) 1
(2) 2
(3) 3
(4) 0
Answer:
(4) 0
Hint: Given, a, b, c, l, m, are in A.P.
a = a; b = a + d; c = a + 2 d; 1 = a + 3d;
m = a + 4d [The general form of A.P.]
a – 4b + 6c – 4l + m
= a – 4(a + d) + 6(a + 2d) – 4 (a + 3d) + a + 4d
= a – 4a – 4d+ 6a + 12 d – 4a – 12d + a + 4d
= a + 6a + a – 4a – 4a
= 8a – 8a
= 0

Question 10.
If a, b, c are in A.P. then \(\frac { a-b }{ b-c } \) is equal to ……………
(1) \(\frac { a }{ b } \)
(2) \(\frac { b }{ c } \)
(3) \(\frac { a }{ c } \)
(4) 1
Answer:
(4) 1
Hint: a, b, c are in A.P.
b – a = c-b [common difference is same t₂ – t₁ = t₃ – t₂]
\(\frac { b-a }{ c-b } \) = 1 ⇒ \(\frac{-(a-b)}{-(b-c)}\) = 1
∴ \(\frac { a-b }{ b-c } \) = 1

Question 11.
If the n^th term of a sequence is 100n + 10, then the sequence is ……
(1) an A.P.
(2) a G..P.
(3) a constant sequence
(4) neither A.P. nor G.P.
Answer:
(1) an A.P.
Hint: t_n = 100/n + 10
t₁ = 100 + 10 = 110
t₂ = 200+ 10 = 210
t₃ = 300+ 10 = 310
∴ The series 110, 210, 310 …………. are in A.P.

Question 12.
If a₁, a₂, a₃, …… are in A.P. such that \(\frac{a_{4}}{a_{7}}=\frac{3}{2}\), then the 13th term of the A.P. is ……………..
(1) \(\frac { 3 }{ 2 } \)
(2) 0
(3) 12a1
(4) 14a1
Answer:
(2) 0
Hint:
\(\frac{a_{4}}{a_{7}}=\frac{3}{2}\)
2a₄ = 3a₇
2(a + 3d) = 3(a + 6d)
2a + 6d = 3a + 18d
0 = a + 12d
[t_n = a + (n – 1)d]
0 = t₁₃

Question 13.
If the sequence a₁, a₂, a₃ ,… is in A.P., then the sequence a₅, a₁₀, a₁₅, …. is …..,
(1) a G.P.
(2) an A.P.
(3) neither A.P nor G.P.
(4) a constant sequence
Answer:
(2) an A.P.
Hint: a₅, a₁₀, a₁₅, ……….. = a + 4d, a + 9d, a + 14d
t₂ – t₁ = a + 9d – (a + 4d) = 5d
t₃ – t₂ = a + 14d – (a + 9d) = 5d
Common difference is 5d
If terms of an A.P are chosen at equal intervals then they form an A.P.

Question 14.
If k + 2,4k – 6, 3k – 2 are the 3 consecutive terms of an A.P, then the value of K is ……………
(1) 2
(2) 3
(3) 4
(4) 5
Answer:
(2) 3
Hint: Here, a = k + 2, b = 4k-6, c = 3k-2
We know that a, b, c are in A.P.
b – a = c – b ⇒ 2b = a + c
2(4k – 6) = k + 2 + 3k – 2
8k – 12 = 4k ⇒ 4k = 12
K = \(\frac { 12 }{ 4 } \) = 3

Question 15.
If a, b, c, l, m, n are in A.P, then 3a + 7, 3b + 7, 3c + 7, 31 + 7, 3m + 7, 3n + 7 form ………..
(1) a G . P.
(2) an A.P.
(3) a constant sequence
(4) neither A.P. nor G.P.
Answer:
(2) an A.P.
Hint: In an A.P, if each term is multiplied by a constant or added by a constant, the resulting sequence is an A.P.

Question 16.
If the third term of a G.P. is 2, then the product of first 5 terms is ……………..
(1) 5²
(2) 2⁵
(3) 10
(4) 15
Answer:
(2) 2⁵
Hint: Consider the 5 terms of the G.P be \(\frac{a}{r^{2}}\),\(\frac { a }{ r } \), a, ar, ar²
Product of 5 terms = \(\frac{a}{r^{2}} \times \frac{a}{r} \times a \times a r \times ar^{2}\), = a⁵, 2⁵ (Given a = 2)

Question 17.
If a, b, c are in G.P., then \(\frac { a-b }{ b-c } \) is equal to …………..
(1) \(\frac { a }{ b } \)
(2) \(\frac { b }{ a } \)
(3) \(\frac { a }{ c } \)
(4) \(\frac { c }{ b } \)
Ans.
(1) \(\frac { a }{ b } \)
Hint: Let the common ratio be “r”

Question 18.
If x, 2x + 2, 3x + 3, are in G.P., then 5x, 10x + 10, 15x + 15, form …………..
(1) anA.P.
(2) a G.P.
(3) a constant sequence
(4) neither A.P. nor a G.P.
Answer:
(2) a G.P.
Hint: If a G.P. is multiplied by a constant then the sequence is also a G.P.
In the given question each term is multiplied by 5

Question 19.
The sequence – 3, – 3, – 3, …… is ……..
(1) an A.P. only
(2) a G.P. only
(3) neither A.P. nor G.P.
(4) both A.P. and G.P.
Answer:
(4) both A.P. and G.P.
Hint: The given sequence is constant.
The sequence is A.P. and G.P.

Question 20.
If the product of the first four consecutive terms of a G.P is 256 and if the common ratio is 4 and the first term is positive, then its 3^rd term is …….
(1) 8
(2) \(\frac { 1 }{ 16 } \)
(3) \(\frac { 1 }{ 32 } \)
(4) 16
Answer:
(1) 8
Hint: The general form of the G.P. is a, ar, ar², ar³, ar⁴, …………..
By data, a (ar) (ar²) (ar³) = 256
a⁴ × r⁶ = 256
[Given r = 4]

Question 21.
In G.P, t₂ = \(\frac { 3 }{ 5 } \) and t₃ = \(\frac { 1 }{ 5 } \) Then the common ratio is ……….
(1) \(\frac { 1 }{ 5 } \)
(2) \(\frac { 1 }{ 3 } \)
(3) 1
(4) 5
Answer:
(2) \(\frac { 1 }{ 3 } \)
Hint: common ratio is
(r) = \(\frac{t_{3}}{t_{2}}=\frac{1}{5} \times \frac{5}{3} \Rightarrow r=\frac{1}{3}\)

Question 22.
If x ≠ 0, then 1 + sec x + sec² x + sec³ x + sec⁴ x + sec⁵ x is equal to ……………
(1) (1 + sec x) (sec² x + sec³ x + sec⁴ x)
(2) (1 + sec x) (1 + sec² x + sec⁴ x)
(3) (1 – sec x) (sec x + sec³ x + sec⁵ x)
(4) (1 + sec x) (1 + sec³ x + sec⁴ x)
Answer:
(2) (1 + sec x) (1 + sec² x + sec⁴ x).
Hint:
1 + sec x + sec² x + sec³ x
+ sec⁴ x + sec⁵ x
= (1 + sex x) + sec² x (1 + sec x) + sec⁴ x (1 + see x)
= (1 + sec x) + sec² x (1 + sec x) + sec⁴ x (1 + secx)
= (1 + sec x) (1 + sec² x + sec⁴ x)

Question 23.
If the n^th term of an A.P. is t_n = 3 – 5n, then the sum of the first n terms is …………….
(1) \(\frac { n }{ 2 } \) [1 – 5n]
(2) n (1 – 5n)
(3) \(\frac { n }{ 2 } \) (1 + 5n)
(4) \(\frac { n }{ 2 } \) (1 + n)
Answer:
(1) \(\frac { n }{ 2 } \) [1 – 5n]
Hint:
t_n =. 3 – 5(n)
t₁ = 3 – 5(1) = -2 ; t₂ = 3 – 10 = -7
a = -2, d = -7 – (-2) = -5
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
= \(\frac { n }{ 2 } \) [-4 + (n – 1) (-5)]
= \(\frac { n }{ 2 } \) [- 4 -5n + 5] = \(\frac { n }{ 2 } \) [1 – 5n]

Question 24.
The common ratio of the G.P. a^m-n, a^m, a^m+n is …………
(1) a^m
(2) a^-m
(3) aⁿ
(4) a^-n
Answer:
(3) aⁿ

Question 25.
If 1 + 2 + 3 + … + n = k then 1³ + 2³ + ……. + n³ is equal to …………
(1) K²
(2) K³
(3) \(\frac{k(k+1)}{2}\)
(4) (K + 1)³
Answer:
(1) K²

II. Answer the following.

Question 1.
Show that the square of any positive integer of the form 3m or 3m + 1 for some integer m.
Answer:
Let a be any positive integer. Then it is of the form 3q or 3q + 1 or 3q + 2
Case – 1 When a = 3q
a² = (3q)² = 9 q²
= (3q) (3q)
= 3m where m = 3q
Case – 2 When a = 3q + 1
a² = (3q + 1)² = 9q² + 6q + 1
= 3q (3q + 2) + 1
= 3 m + 1
where m = q (3q + 2)
Case – 3 When a = 3q + 2
a² = (3q + 2)² = 9q² + 12q + 4
= 9q² + 12q + 3 + 1
= 3(3q² + 4q + 1) + 1
= 3m + 1
where m = 3q² + 4q + 1
Hence a is of the form 3m or 3m + 1

Question 2.
Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.
Solution:
Let us start with taking a, where a is a +ve odd integer.
We apply the division algorithm with ‘a’ and ‘b’ = 4.
Since 0 < r < 4, the possible remainders are 0, 1, 2, 3.
That is, a can be 4q, or 4q + 1, or 4q + 2 or 4q + 3, where 1 is the quotient. However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Any odd integer is of the form 4q + 1 or 4q + 3.

Question 3.
Compute x such that 5⁴ = x (mod 8)
Answer:
5² = 25 = 1 (mod 8)
5⁴ = (5²)² = l² (mod 8)
= 1
5⁴ = 1 (mod 8)

Question 4.
The first term of an A.P. is 6 and the common difference is 5. Find the A.P. and its general term.
Answer:
Given, a = 6, d = 5
General term t_n = a + (n – 1) d
= 6 + (n – 1) 5
= 6 + 5 n – 5
= 5 n + 1
The general form of the A.P. is a, a + d, a + 2d,
The A.P. is 6, 11, 16, 21, ……… 5n + 1.

Question 5.
Which term of the arithmetic sequence 24, 23\(\frac { 1 }{ 4 } \), 22 \(\frac { 1 }{ 2 } \), 21 \(\frac { 3 }{ 4 } \), …….. is 3?
Answer:
Given The A.P is 24, 23 \(\frac { 1 }{ 4 } \), 22 \(\frac { 1 }{ 2 } \), 21 \(\frac { 3 }{ 4 } \), …………..

Question 6.
Determine the AP whose 3rd term is 5 and the 7th term is 9.
Solution:
We have
a₃ = a + (3 – 1)d = a + 2d = 5 ……….. (1)
a₇ = a + (7 – 1)d = a + 6d = 9 ………… (2)
(1) – (2) ⇒ -4d = -4 ⇒ d = 1.
Sub, d = 1 in (1), we get
a + 2(1) = 5
a = 3
Hence the required A.P. is 3, 4, 5, 6, 7.

Question 7.
If a, b, c are in A.P. then prove that (a – c)² = 4 (b² – ac).
Answer:
Given a, b, c are in A.P.
n = 10
∴ b – a = c – b
2 b = a + c
Squaring on both sides,
(a + c)² = (2b)²
a² + c² + 2ac = 4b²
(a – c)² + 2ac + 2ac = 4b²
[a² + c² = (a – c)² + 2ac]
(a – c)² = 4b² – 4ac
(a – c)² = 4(b² – ac)
Hence it is proved.
Aliter: Given a, b, c are in A.P.
b – a = c – b
2b = a + c
To prove, (a – c)² = 4(b² – ac)
L.H.S.= (a – c)²
= a² + c² – 2 ac
= (a + c)² – 2 ac – 2ac
= (a + c)² – 4ac
= (2b)² – 4ac (2b = a + c)
= 4b² – 4ac = 4 (b² – ac) = R.H.S
∴ L.H.S = R.H.S., Hence proved.

Question 8.
If the sum of the first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.
Solution:
Here S₁₄ = 1050
n = 14
a = 10
S_n = \(\frac { n }{ 2 } \) (2a + (n – 1)d)
1050 = \(\frac { 14 }{ 2 } \) (20 + 13d)
= 140 + 91d
910 = 91d
d = 10
a₂₀ = 10 + (20 – 1) × 10
= 20
∴ 20th term = 200.

Question 9.
Find the sum of the first 40 terms of the series 1² – 2² + 3² – 4² + ….
Answer:
The given series is 1² – 2² + 3² – 4² + …. 40 terms
Grouping the terms we get,
(1² – 2²) + (3² – 4²) + (5² – 6²) + ………….. 20 terms
(1 – 4) + (9 – 16) + (25 – 36) + …………… 20 terms
(- 3) + (- 7) + (- 11) + ………………. 20 term
This is an A.P
Here a = – 3, d = – 7 – (-3) = – 7 + 3 = – 4 n = 20
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1) d ]
S₂₀ = \(\frac { 20 }{ 2 } \) [2(-3) + 19(-4)]
= 10 (- 6 – 76) = 10 (- 82) = – 820
∴ Sum of 40 terms of the series is – 820.
Aliter. 1² – 2² + 3² – 4² + …….. + 39² – 40²
= 1² + 3² + 5² + ……. + 39² –
(2² + 4² + 6² + ……….. + 40²)
= 1² + 2² + 3² + 4² + …. + 40²
– (2² + 4² + 6² + …. + 40²)
– (2² + 4² + 6² + …. + 40²)
= 1² + 2² + 3² + …. + 40²
= 2 × 2² (1² + 2² + ….. + 20²)

Question 10.
Find the sum of first 24 terms of the list of numbers whose nth term is given by
a_n = 3 + 2n.
Solution:
a_n = 3 + 2n
a₁ = 3 + 2 = 5
a₂ = 3 + 2 × 2 = 7
a₃ = 3 + 2 × 3 = 9
List of numbers becomes 5, 7, 9. 11, ……….
Here,7 – 5 = 9 – 7 = 11 – 9 = 2 and soon. So, it forms an A.P. with common difference d = 2.
To find S₂₄, we have n = 24, a = 5, d = 2.
S₂₄ = \(\frac { 24 }{ 2 } \) [2 × 5 + (24 – 1) × 2 ]
= 12 [10 + 46] = 672
So, sum of first 24 terms of the list of numbers is 672.

Question 11.
If a clock strikes once at 1 o’clock, twice at 2 o’clock and so on, how many times will it strike in a day?
Answer:
Number of times the clock strikes each hour form an A.P.
Number of times strike in 12 hours is
1 + 2 + 3 + …….. + 12
Here, a = 1, d = 1, n = 12, l = 12
S_n = \(\frac { n }{ 2 } \) (a + l) = \(\frac { 12 }{ 2 } \) (1 + 12)
= 6 × 13 = 78 times
∴ Number of times the clock strike in 24 hours
= 78 × 2 = 156 times.

Question 12.
If the 4^th and 7^th terms of a G.P. are 54 and 1458 respectively, find the G.P.
Answer:
Given, t₄ = 54 and t₇ = 1458

Substituting the value of r = 3 in (1)
a × 27 = 54
a = \(\frac { 54 }{ 27 } \) = 2
∴ The Geometric sequence is 2, 6, 18, 54 ………

Question 13.
Which term of the geometric sequence,
(i) 5, 2, \(\frac { 4 }{ 5 } \), \(\frac { 8 }{ 25 } \), ……… is \(\frac { 128 }{ 15625 } \)?
Answer:
The given G.P. is 5, 2, \(\frac { 4 }{ 5 } \),\(\frac { 8 }{ 25 } \), …….., is \(\frac { 128 }{ 15625 } \)
Here a = 5, r = \(\frac { 2 }{ 5 } \), t_n = \(\frac { 128 }{ 15625 } \)
t_n = a.r^n-1

Question 14.
How many consecutive terms starting from the first term of the series 2 + 6 + 18 + … would sum to 728?
Answer:
The given series is
2 + 6 + 18 + …. + t_n = 728
Here a = 2, r = = 3, S_n = 728

∴ Required number of terms = 6

Question 15.
A geometric series consists of four terms and has a positive common ratio. The sum of the first two terms is 9 and sum of the last two terms is 36. Find the series.
Answer:
Let the four terms of the G.P. be a, ar, ar² and ar³ ……….
Given, a + ar = 9 ……(1)
ar² + ar³ = 36
r² (a + ar) = 36
r² (9) = 36
[from (1)]
r² = =4
r = ± 2
then r = 2
(given common positive ratio)
a + a (2) = 9 from (1)
3a = 9
a = 3
∴ The required series
= 3 + 3(2) + 3 (2²) + 3 (2³) + ……
= 3 + 6 + 12 + 24 + ……..

Question 16.
Suppose that five people are ill during the first week of an epidemic and each sick person spreads the contagious disease to four other people by the end of the second week and so on. By the end of 15^th week, how many people will be affected by the epidemic?
Answer:
Number of people affected by the epidemic during each week form a geometric series.
S₁₅ = 5 + (4 × 5) + (4 × 20) + (4 × 80) + …. 15 terms
= 5 + 20 + 80 + 320 + … 15 terms
Here a = 5, r = 4, n = 15

Question 17.
A gardener wanted to reward a boy for his good deeds by giving some mangoes. He gave the boy two choices. He could either have 1000 mangoes at once or he could get 1 mango on the first day, 2 on the second day, 4 on the third day, 8 mangoes on the fourth day and so on for ten days. Which option should the boy choose to get the maximum number of mangoes?
Answer:
I choice
The boy could get 1000 mangoes at once
II choice
The boy receives mangoes daily for ten days
S₁₀ = 1 + 2 + 4 + 8 + ……… 10 terms

Question 18.
Find the value of k if
1³ + 2³ + 3³ + ….. + K³ = 2025
Answer:
Given, 1³ + 2³ + 3³ + … + K³ = 2025

Question 19.
If 1³ + 2³ + 3³ + …… + K³ = 8281, then find 1 + 2 + 3 + … + K.
Answer:
Given, 1³ + 2³ + 3³ + …… + K³ = 8281

1 + 2 + 3 + …… + K = 91

Question 20.
Find the sum of all 11 term of an AP whose middle most term in 30.
Answer:
Let ‘a’ be the first term and ‘d’ be the common difference of the give A.P.
Middle most term = (\(\frac { 11+1 }{ 2 } \))^th = 6^th term
t_n = a + (n – 1)d
t₆ = a + 5d
a + 5d = 30
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
S₁₁ = \(\frac { 11 }{ 2 } \) [2a + 10d]
= \(\frac { 11 }{ 2 } \) × 2 [a + 5d]
= 11 × 30
= 330
Sum of 11 terms = 330

III. Answer the following.

Question 1.
Use Euclid’s division algorithm to find the HCF of 867 and 255.
Answer:
Here 867 > 255
Applying Euclid’s Lemma to 867 and 255 we get

867 = (255 × 3) + 102
The remainder 102 ≠ 0
Again applying Euclid’s
Lemma to 255 and 102
255 = 102 × 2 + 51
The remainder 51 ≠ 0
Again applying Euclid’s
Lemma to 102 and 51 we get
102 = 51 × 2 + 0
The remainder is 0
∴ HCF of 867 and 255 is 51

Question 2.
Find the number of integer solutions of 5x = 2 (mod 13)
Answer:
5x ≡ 2 (mod 13) can be written as
5x – 2 = 13 k for some integer
5x = 13 k + 2
x = \(\frac{13 k+2}{5}\)
Since 5k is an integer \(\frac{13 k+2}{5}\) cannot be an inter.
There is no integer solution.

Question 3.
Find the 40^th term of A.P. whose 9^th term is 465 and 20^th term is 388.
Answer:
t_n = a + (n – 1) d
t₉ = a + 8d (t₉ = 465)
a + 8d = 465 ……(1)

Substitute the value of d = -7 in (1)
a + 8(-7) = 465
a – 56 = 465
a = 465 + 56 = 521
a = 521, d = -7, n = 40
t₄₀ = 521 + 39(-7)
= 521 – 273
= 248
40^th term of an A.P. is 248

Question 4.
Find the three consecutive terms in an A.P. whose sum is 18 and the sum of their squares is 140.
Answer:
Let the three consecutive terms in an
A.P. be m – d,m,m + d
By the given data,
Sum of threee terms = 18
m – d + m + m + d = 18
3m = 18
m = \(\frac { 18 }{ 3 } \) = 6
Again by the given data,
Sum of their squares = 140
(m – d)² + m² + (m + d)² = 140
m² + d² – 2md + m² + m² + d² + 2md = 140
3m² + 2d² = 140
3(62) + 2d² = 140
3(36) + 2d² = 140
2d² = 140 – 108
2d² = 32
d² = \(\frac { 32 }{ 2 } \) = 16
∴ d = ± 4
when, m = 6, d = + 4
m – d = 6 – 4 = 2
m = 6
m + d = 6 + 4 = 10
when, m = 6, d = -4
m – d = 6-(-4) = 6 + 4= 10
m = 6
m + d = 6 +(-4) = 6 – 4 = 2
∴ The three numbers are 2, 6 and 10 or 10, 6,2.

Question 5.
If m times the m^th term of an A.P. is equal to n times its n^th term, then show that the (m + n)^th term of the A.P. is zero.
Answer:
Given, mt_m = nt_n
m[a + (m – 1) d] = n [a + (n – 1) d]
[we know that t_n = a + (n – 1)d]
m[a + md – d] = n[a + nd – d]
ma + m²d – md = na + n²d – nd
ma – na + m²d – n²d = md – nd
a (m – n) + d (m² – n²) = d(m – n)
a (m – n) + d(m + n)(m – n) = d(m – n) ÷ by (m – n) on both sides,
a + d (m + n) = d
a + d(m + n) – d = 0
a + d(m + n – 1) = 0 ….. (1)
To prove, t_(m+n) = 0
t_(m+n) = a + (m + n – 1)d
t_(m+n) = 0(from(1))
Hence it is proved.

Question 6.
If a, b, c are in A.P. then prove that (a – c)² = 4 (b² – ac).
Answer:
Given a, b, c are in A.P.
∴ b – a = c – b
2 b = a + c
Squaring on both sides,
(a + c)² = (2b)²
a² + c² + 2 ac = 4 b²
(a – c)² + 2 ac + 2 ac = 4 b²
[a² + c² = (a – c)² + 2 ac]
(a – c)² = 4b² – 4ac
(a – c)² = 4 (b² – ac)
Hence it is proved.
Aliter: Given a, b, c are in A.P.
b – a = c – b
2 b = a + c
To prove, (a – c)² = 4(b² – ac)
L.H.S. = (a – c)²
= a² + c² – 2ab
= (a + c)² – 2ac – 2ac
= (a + c)² – 4ac
= (2b)² – 4ac (2b = a + c)
= 4 b² – 4ac = 4 (b² – ac) = R.H.S
∴ L.H.S = R.H.S., Hence proved.

Question 7.
The ratio of the sums of first m and first n terms of an arithmetic series is m² : n² show that the ratio of the m^th and n^th terms is (2m – 1) : (2n -1).
Answer:

n[2a + (m – 1) d] = tn[2a + nd-d]
2 an + mnd- nd = 2 am + mnd— md 2an-2am = nd- md 2 a (n-m) = d(n- m)
÷ by (n – m) on both sides,
2a = d
To prove, t_m : t_n = (2m – 1) : (2n – 1)
L.H.S = t_m : t_n
= a + (m – 1) d : a + (n – 1)d
= a + (m – 1) 2a : a + (n – 1)2a
[Substitute the value of d = 2a]
= a + 2 am – 2 a: a + 2 am – 2a
= 2am – a : 2an – a
= a (2m – 1) : a (2n – 1)
= (2m – 1) : (2n – 1) = R. H. S
= (2m – 1) : (2n – 1)
∴ t_m : t_n
L.H.S = R.H.S
Hence it is proved.

Question 8.
A construction company will be penalised each day for delay in construction of a bridge. The penalty will be ₹4000 for the first day and will increase by ₹1000 for each following day. Based on its budget, the company can afford to pay a maximum of ₹1,65,000 towards penalty. Find the maximum number of days by which the completion of work can be delayed.
Solution:
Penalty for the first day (a) = ₹ 4000
Increased rate for every day (d) = ₹ 1000
Maximum amount of penalty (S_n)
= ₹ 1,65,000
S_n = \(\frac { n }{ 2 } \) [2a + (n-1) 1000]
165000 = \(\frac { n }{ 2 } \) [2(4000) + (n – 1) 1000]
= \(\frac { n }{ 2 } \) [8000 + 1000 n – 1000]
165000 = \(\frac { n }{ 2 } \) (7000 + 1000n)
330000 = 7000 n + 1000 n²
0 = 1000 n² + 7000 n – 330000 ÷ 1000 on both sides,
n² + 7n – 330 = 0
(n + 22) (n – 15) = 0
n = -22 or n = 15
n = -22 (not possible)
∴ Maximum number of days for which the work can be delayed is 15 days.

Question 9.
If the product of three consecutive terms in G.P. is 216 and sum of their products in pairs is 156, find them.
Let the three consecutive terms of G.P. be \(\frac { a }{ r } \), a, ar.
Product of three terms = 216
\(\frac { a }{ r } \) × a × ar = 216
a³ = 216
a³ = 63
a = 6
Sum of their products in pairs = 156

Question 10.
If a, b, c, d are in a geometric sequence, then show that
(a – b + c) (b + c + d) = ab + bc + cd.
Answer:
Given, a, b, c, d are in a geometric sequence.
Let a = a, b = ar, c = ar², d = ar³
To prove, (a – b + c) (b + c + d) = ab + bc + cd
L.H.S. = (a – b + c)(b + c + d)
= (a – ar + ar²) (ar + ar² + ar³ )
= a (1 – r + r²)ar (1 + r + r²)
= a²r (1 – r + r²) (1 + r + r²)
= a²r (1 + r² + r4)
= a²r + a²r³ + a²r⁵
= a (ar) + ar (ar²) + ar² (ar³)
= ab + bc + cd
= R.H.S.
L.H.S. = R.H.S., Hence proved.

Question 11.
Find the sum of the first n terms of the series 0.4 + 0.94 + 0.994 + ………..
Answer:
Given series is 0.4 + 0.94 + 0.994 + ……………. + n terms.
S_n = 0.4 + 0.94 + 0.994 + ……….. + n terms

Question 12.
Find the total area of 12 squares whose sides are 12 cm, 13 cm,… 23 cm respectively.
Answer:
Given, the sides of 12 squares are 12 cm, 13 cm, 14 cm,… 23 cm
Total area of 12 squares
= 12² + 13² + 14² + … + 23²
= (1² + 2² + 3² … + 23²) – (1² + 2² + … + 11²)

Students can download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Reduce each of the following rational expression to its lowest form.
(i) \(\frac{x^{2}-1}{x^{2}+x}\)
Answer:
\(\frac{x^{2}-1}{x^{2}+x}\) = \(\frac{(x+1)(x-1)}{x(x+1)}\) = \(\frac { x-1 }{ x } \)

(ii) \(\frac{x^{2}-11 x+18}{x^{2}-4 x+4}\)

x² – 11x + 18 = (x – 9) (x – 2)
x² – 4x + 4 = (x – 2) (x – 2)

(iii) \(\frac{9 x^{2}+81 x}{x^{3}+8 x^{2}-9 x}\)
9x² + 81x = 9x(x + 9)
x³ + 8x² – 9x = x(x² + 8x – 9)
= x (x + 9) (x – 1)

(iv) \(\frac{p^{2}-3 p-40}{2 p^{3}-24 p^{2}+64 p}\)
p² – 3p – 40 = (p – 8) (p + 5)
2p³ – 24p² + 64p = 2p (p² – 12p + 32)
= 2p (p – 8) (p – 4)

Question 2.
Find the excluded values , if any of the following expressions.

(i) \(\frac{y}{y^{2}-25}\)
Answer:
The expression \(\frac{y}{y^{2}-25}\) is undefined
when y² – 25 = 0
y² – 5² = 0
(y + 5) (y – 5) = 0
y + 5 = 0 or y – 5 = 0
∵ y = -5 or y = 5
The excluded values are -5 and 5

(ii) \(\frac{t}{t^{2}-5 t+6}\)
Answer:
The expression \(\frac{t}{t^{2}-5 t+6}\) is undefined
when t² – 5t + 6 = 0
(t – 3) (t – 2) = 0

t – 3 = 0 or t – 2 = 0
t = 3 or t = 2
The excluded values are 2 and 3

(iii) \(\frac{x^{2}+6 x+8}{x^{2}+x-2}\)
Answer:
x² + 6x + 8 = (x + 4) (x + 2)
x² + x – 2 = (x + 2) (x – 1)


The expression \(\frac { x+4 }{ x-1 } \) is undefined
when x – 1 = 0
∵ x = 1
The excluded value is 1

(iv) \(\frac{x^{3}-27}{x^{3}+x^{2}-6 x}\)
x³ – 27 = x³ – 3³
= (x – 3) (x² + x + 3)
x³ + x² – 6x = x(x² + x – 6) = x (x + 3) (x – 2)


when x (x + 3) (x – 2) = 0
x = 0 or x + 3 = 0 or x – 2 = 0
x = 0 or x = -3 or x = 2
The excluded values are 0 , -3 and 2

Students can download Maths Chapter 3 Algebra Ex 3.12 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.12

Question 1.
Solve by the method of elimination
(i) 2x – y = 3; 3x + y = 7
Solution:
2x – y = 3 → (1)
3x + y = 7 → (2)
By adding (1) and (2)
5x + 0 = 10
x = \(\frac{10}{5}\)
x = 2
Substitute the value of x = 2 in (1)
2(2) – y = 3
4 – y = 3
-y = 3 – 4
-y = -1
y = 1
The value of x = 2 and y = 1

(ii) x – y = 5; 3x + 2y = 25
Solution:
x – y = 5 → (1)
3x + 2y = 25 → (2)
(1) × 2 ⇒ 2x – 2y = 10 → (3)
(2) × 1 ⇒ 3x + 2y = 25 → (2)
(3) + (2) ⇒ 5x + 0 = 35
x = \(\frac{35}{5}\)
= 7
Substitute the value of x = 7 in (1)
x – y = 5
7 – y = 5
-y = 5 – 7
-y = -2
y = 2
∴ The value of x = 7 and y = 2

(iii) \(\frac{x}{10}\) + \(\frac{y}{5}\) = 14; \(\frac{x}{8}\) + \(\frac{y}{6}\) = 15
Solution:
\(\frac{x}{10}\) + \(\frac{y}{5}\) = 14
LCM of 10 and 5 is 10
Multiply by 10
x + 2y = 140 → (1)
\(\frac{x}{8}\) + \(\frac{y}{6}\) = 15
LCM of 8 and 6 is 24
3x + 4y = 360 → (2)
(1) × 2 ⇒ 2x + 4y = 280 → (3)
(2) × 1 ⇒ 3x + 4y = 360 → (2)
(3) – (2) ⇒ -x + 0 = -80
∴ x = 80
Substitute the value of x = 80 in (1)
x + 2y = 140
80 + 2y = 140
2y = 140 – 80
2y = 60
y = \(\frac{60}{2}\)
y = 30
∴ The value of x = 80 and y = 30

(iv) 3(2x + y) = 7xy; 3(x + 3y) = 11xy
Solution:
3(2x + y) = 7xy
6x + 3y = 7xy
Divided by xy

3a + 6b = 7 → (1)
3(x + 3y) = 11xy
3x + 9y = 11xy
Divided by xy

9a + 3b = 11 → (2)
(1) × 3 ⇒ 9a + 18b = 21 → (3)
(2) × 1 ⇒ 9a + 3b = -11 → (2)
(3) – (2) ⇒ 15b = 10
b = \(\frac{10}{15}\) = \(\frac{2}{3}\)
Substitute the value of b = \(\frac{2}{3}\) in (1)
3a + 6 × \(\frac{2}{3}\) = 7
3a + 4 = 7
3a = 7 – 4
3a = 3
a = \(\frac{3}{3}\)
= 1
But \(\frac{1}{x}\) = a
\(\frac{1}{x}\) = 1
x = 1
But \(\frac{1}{y}\) = b
\(\frac{1}{y}\) = \(\frac{2}{3}\)
2y = 3
y = \(\frac{3}{2}\)
∴ The value of x = 1 and y = \(\frac{3}{2}\)

(v) \(\frac{4}{x}\) + 5y = 7; \(\frac{3}{x}\) + 4y = 5
Solution:
Let \(\frac{1}{x}\) = a
4a + 5y = 7 → (1)
3a + 4y = 5 → (2)
(1) × 4 ⇒ 16a + 20y = 28 →(3)
(2) × 5 ⇒ 15a + 20y = 25 → (4)
(3) – (4) ⇒ a + 0 = 3
a = 3
Substitute the value of a = 3 in (1)
4(3) + 5y = 7
5y = 7 – 12
5y = -5
5y = \(\frac{-5}{5}\) = -1
But \(\frac{1}{x}\) = a
\(\frac{1}{x}\) = 3
3x = 1 ⇒ x = \(\frac{1}{3}\)
The value of x = \(\frac{1}{3}\) and y = -1

(vi) 13x + 11y = 70; 11x + 13y = 74
Solution:
13x + 11y = 70 → (1)
11x + 13y = 74 → (2)
(1) + (2) ⇒ 24x + 24y = 144
x + y = 6 → (3) (Divided by 24)
(1) – (2) ⇒ 2x – 2y = -4
x – y = -2 → (4) (Divided by 2)
(4) + (3) ⇒ 2x = 4
x = \(\frac{4}{2}\)
= 2
Substitute the value x = 2 in (3)
2 + y = 6
y = 6 – 2
= 4
∴ The value of x = 2 and y = 4

Question 2.
The monthly income of A and B are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves Rs 5,000 per month, find the monthly income of each.
Solution:
Let the income of “A” be “x” and the income of “B” be “y”.
By the given first condition
x : y = 3 : 4
4x = 3y (Product of the extreme is equal to the product of the means)
4x – 3y = 0 → (1)
Expenditure of A = x – 5000
Expenditure of B = y – 5000
By the given second condition
x – 5000 : y – 5000 = 5 : 7
7(x – 5000) = 5(y – 5000)
7x – 35000 = 5y – 25000
7x – 5y = -25000 + 35000
7x – 5y = 10000 → (2)
(1) × 5 ⇒ 20x – 15y = 0 → (3)
(2) × 3 ⇒ 21x – 15y = 30000 → (4)
(3) – (4) ⇒ x + 0 = 30000
x = 30000
Substitute the value of x in (1)
4 (30000) – 3y = 0
120000 = 3y
y = \(\frac{120000}{3}\) = 40000
∴ Monthly income of A is Rs 30,000
Monthly income of B is Rs 40,000

Question 3.
Five years ago, a man was seven times as old as his son, while five year hence, the man will be four times as old as his son. Find their present age.
Solution:
Let the age of a man be “x” and the age of a son be “y”
5 years ago
Age of a man = x – 5 years
Age of his son = y – 5 years
By the given first condition
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x – 7y = -35 + 5
x – 7y = -30 → (1)
Five years hence
Age of a man = x + 5 years
Age of his son = y + 5 years
By the given second condition
x + 5 = 4 (y + 5)
x + 5 = 4y + 20
x – 4y = 20 – 5
x – 4y = 15 → (2)
(1) – (2) ⇒ -3y = -45
3y = 45
y = \(\frac{45}{3}\)
= 15
Substitute the value of y = 15 in (1)
x – 7(15) = -30
x – 105 = -30
x = -30 + 105
= 75
Age of the man is 75 years
Age of his son is 15 years

Students can download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.3

Question 1.
Find the LCM and GCD for the following and verify that f(x) × g(x) = LCM × GCD

(i) 21x²y, 35xy²
Answer:
p(x) = 21 x²y = 3 × 7 × x² × y
g(x) = 35xy² = 5 × 7 × x × y²
G.C.D = 7 xy
L.C.M = 3 × 5 × 7 x² × y²
= 105 x²y²
L.C.M × G.C.D = 105x²y² × 7xy
= 735 x³y³ ….(1)
p(x) × g(x) = 21x²y × 35xy²
= 735x³y³ ….(2)
From (1) and (2) we get
L.C.M × G.C.D. = p(x) × g(x)

(ii) (x³ – 1)(x + 1),(x³ + 1)
Answer:
p(x) = (x³ – 1) (x + 1) = (x – 1) (x² + x + 1) (x + 1)
g(x) = x³ + 1 = (x + 1) (x² – x + 1)
G.C.D = (x + 1)
L.C.M = (x + 1) (x – 1) (x² + x + 1) (x² – x + 1)
L.C.M × G.C.D = (x + 1) (x – 1)(x² + x + 1)(x² – x + 1)x(x + 1)
= (x + 1)² (x – 1) (x² + x + 1) (x² – x + 1) ……….(1)
p(x) × g(x) = (x – 1) (x² + x + 1) (x + 1) (x + 1) (x² – x + 1)
= (x + 1)² (x – 1) (x² + x + 1) (x² – x + 1) ……….(2)
From (1) and (2) we get
L.C.M × G.C.D. = p(x) × g(x)

(iii) (x²y + xy²), (x² + xy)
Answer:
p(x) = x²y + xy² = xy(x + y)
g(x) = x² + xy = x(x + y)
G.C.D = x(x+y)
L.C.M = xy (x +y).
L.C.M × G.C.D = xy(x + y) × x(x + y)
= x²y(x + y)² …..(1)
p(x) × g(x) = xy(x + y) × x(x + y)
= x²y(x + y)²
From (1) and (2) we get
L.C.M × G.C.D. = p(x) × g(x)

Question 2.
Find the LCM of each pair of the following polynomials
(i) a² + 4a – 12, a² – 5a + 6 whose GCD is a – 2
Answer:
p(x) = a² + 4a – 12
= a² + 6a – 2a – 12
= a (a + 6) – 2(a + 6)
= (a + 6) (a – 2)

g(x) = a² – 5a + 6
= a² – 3a – 2a + 6

= a(a – 3) – 2 (a – 3)
= (a – 3) (a – 2)

(ii) x⁴ – 27a³x, (x – 3a)² whose GCD is (x – 3a)
Answer:
p(x) = x⁴ – 27a³x = x[x³ – 27a³]
= x[x³ – (3a)³]
= x(x – 3a) (x² + 3ax + 9a²)
g(x) = (x – 3a)²
G.C.D. = x – 3a

L.C.M. = x (x – 3a)² (x² + 3ax + 9a²)

Question 3.
Find the GCD of each pair of the following polynomials
(i) 12(x⁴ – x³), 8(x⁴ – 3x³ + 2x²) whose LCM is 24x³ (x – 1)(x – 2)
Answer:
p(x) = 12(x⁴ – x³)
= 12x³(x- 1)
g(x) = 8(x⁴ – 3x³ + 2x²)

= 8x²(x² – 3x + 2)
= 8x²(x – 2)(x – 1)
L.C.M. = 24x³ (x – 1) (x – 2)

(ii) (x³ + y³), (x⁴ + x²y² + y⁴) whose LCM is (x³ + y³) (x² + xy + y²)
Answer:
p(x) = x³ + y³
= (x + y)(x² – xy + y²)
g(x) = x⁴ + x²y² + y⁴ = [x² + y²]² – (xy)²
= (x² + y² + xy) (x² + y² – xy)
L.C.M. = (x³ + y³) (x² + xy + y²)
(x + y) (x² – xy + y²) (x² + xy + y²)

G.C.D. = x² – xy + y²

Question 4.
Given the L.C.M and G.C.D of the two polynomials p(x) and q(x) find the unknown polynomial in the following table

Answer:
L.C.M. = a³ – 10a² + 11a + 70
= (a – 7) (a² – 3a – 10)
= (a – 7) (a – 5) (a + 2)

G.C.D. = (a – 7)
p(x) = a² -12a + 35
= (a – 5)(a – 7)

q(x) = \(\frac{\mathrm{LCM} \times \mathrm{GCD}}{p(x)}\)

(ii) L.C.M (x² + y²)(x⁴ + x²y² + y⁴)
(x² + y²)[(x² + y²)²-(xy)²]
(x² + y²) (x² + y² + xy) (x² + y² – xy)
G.C.D. = x² – y²
(x + y)(x – y)
q(x) = (x⁴ – y⁴) (x² + y² – xy)
= [(x²)² – (y²)²](x² + y² – xy)
= (x² + y²) (x² – y²) (x² + y² – xy)
(x² + y²) (x + y) (x – y) (x² + y² – xy)
P(x) = x² + y² + xy

Students can download Maths Chapter 3 Algebra Ex 3.11 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.11

Question 1.
Solve, using the method of substitution.
(i) 2x – 3y – 7; 5x + y = 9
Solution:
2x – 3y = 7 → (1)
5x + y = 9 → (2)
Equation (2) becomes
y = 9 – 5x
Substitute the value of y in (1)
2x – 3 (9 – 5x) = 7
2x – 27 + 15x = 7
17x = 7 + 27
17x = 34
x = \( \frac{34}{17}\)
= 2
Substitute the value of x = 2 (in) (2)
y = 9 – 5 (2) = 9 – 10 = -1
∴ The value of x = 2 and y = -1

(ii) 1.5x + 0.1y = 6.2; 3x – 0.4y = 11.2
Solution:
1.5x + 0.1y = 6.2
Multiply by 10
15x + y = 62
y = 62 – 15x → (1)
3x – 0.4y = 11.2
Multiply by 10
30x – 4y = 112
divided by (2) we get
15x – 2y = 56 → (2)
Substitute the value of y in (2)
15x – 2(62 – 15x) = 56
15x – 124 + 30x = 56
45x = 56 + 124
45x = 180
x = \( \frac{180}{45}\)
= 4
Substitute the value of x = 4 in (1)
y = 62 – 15(4)
= 62 – 60
y = 2
∴ The value of x = 4 and y = 2

(iii) 10% of x + 20% of y = 24; 3x – y = 20
Solution:
\( \frac{10}{100}\) × x + \( \frac{20}{100}\) × y = 24
\( \frac{x}{10}\) + \( \frac{y}{5}\) = 24
Multiply by 10
x + 2y = 240 → (1)
3x – y = 20
– y = 20 – 3x
y = 3x – 20 → (2)
Substitute the value of y in (1)
x + 2 (3x – 20) = 240
x + 6x – 40 = 240
7x – 40 = 240
7x = 240 + 40
7x = 280
x = \( \frac{280}{7}\)
x = 40
Substitute the value of x = 40 in (2)
y = 3 (40) – 20 = 120 – 20
y = 100
∴ The value of x = 40 and y = 100

(iv) √2x – √3y = 1; √3x – √8y = 0
Solution:
√2x – √3y = 1
– √3y = 1 – √2x
√3y = √2x – 1
y = \(\frac{√2x-1}{√3}\) → (1)
√3x – √8y = 0 → (2)
Substitute the value of y in (2)
\(\sqrt{3x}-\frac{√8(√2x-1)}{√3}\)
multiply by √3
⇒ \(\frac{3x-√8(√2x-1)}{√3}\)
3x – √8(√2x – 1) = 0
3x – 4x + √8 = 0
-x = √8
Substitute the value of x in (1)

The value of x = √8 and y = √3

Question 2.
Raman’s age is three times the sum of the ages of his two sons. After 5 years his age will be twice the sum of the ages of his two sons. Find the age of Raman.
Solution:
Let Raman’s age be “x” years and the sum of the ages of two sons be “y” years.
By the given first condition
x = 3y
x – 3y = 0 → (1)
After 5 years Raman’s age is x + 5 years
Sum of sons age is (y + 10) years
(each son age increases by 5 years)
By the given second condition
x + 5 = 2 (y + 10)
x + 5 = 2y + 20
x – 2y = 20 – 5
x – 2y = 15 → (2)
Equation (1) becomes
x = 3y
Substitute the value of x in (2)
3y – 2y = 15
y = 15
Substitute the value of y = 15 in x = 3y
x = 3(15)
x = 45
∴ Raman’s age = 45 years

Question 3.
The middle digit of a number between 100 and 1000 is zero and the sum of the other digit is 13. If the digits are reversed, the number so formed exceeds the original number by 495. Find the number.
Solution:
Let the unit digit be and the 100 is digit be X. The number is XOY (100x + y)
By the given first condition
x + y = 13 ….(1)
If the digits are reversed the number is 100 y + x.
By the given second condition.
100y + x = 100x + y + 495
-99x + 99y = 495
-x + y = 5 …. (2)
x + y = 13 ….(1)
Add (1) and (2)
2y = 18
y = 9
Substitute the value of y = 9 in (1)
x + 9 = 13
x = 13 – 9
x = 4
∴ The number is 409

Students can download Maths Chapter 3 Algebra Ex 3.10 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.10

Question 1.
Draw the graph for the following:
(i) y = 2x
Solution:
When x = -2, y = 2 (-2) = -4
When x = 0, y = 2 (0) = 0
When x = 2, y = 2 (2) = 4
When x = 3, y = 2 (3) = 6

Plot the points (-2, -4) (0, 0) (2, 4) and (3, 6) in the graph sheet we get a straight line.

(ii) y = 4x – 1
Solution:
When x = – 1; y = 4 (-1) -1 ⇒ y = -5
When x = 0; y = 4 (0) – 1 = 0 – 1 ⇒ y = -1
When x = 2; y = 4 (2) -1 = 8 – 1 ⇒ y = l

Plot the points (-1, -5) (0, -1) and (2, 7) in the graph sheet we get a straight line. At the time of printing change the direction.

(iii) y = (\(\frac{3}{2}\))x + 3
Solution:
When x = -2;
y = \(\frac{3}{2}\)(-2) + 3
y = -3 + 3 = 0
when x = 0;
y = \(\frac{3}{2}\)(0) + 3
y = 3
when x = 2;
y = \(\frac{3}{2}\)(2) + 3
y = 3 + 3
= 6


Plot the points (-2, 0) (0, 3) and (2, 6) in the graph sheet we get a straight line.

(iv) 3x + 2y = 14
Solution:
y = \(\frac{-3x+14}{2}\)
y = – \(\frac{3}{2}\)x + 7
when x = -2
y = –\(\frac{3}{2}\)(-2) + 7 = 10
when x = 0
y = –\(\frac{3}{2}\)(0) + 7 = 7
when x = 2
y = –\(\frac{3}{2}\)(2) + 7 = 4


Plot the points (-2, 10) (0, 7) and (2, 4) in the graph sheet we get a straight line.

Question 2.
Solve graphically (i) x + y = 7, x – y = 3
Solution:
x + y = 7
y = 7 – x

Plot the points (-2, 9), (0, 7) and (3, 4) in the graph sheet
x – y = 3
-y = -x + 3
y = x – 3

Plot the points (-2, -5), (0, -3) and (4, 1) in the same graph sheet.

The point of intersection is (5, 2) of lines (1) and (2).
The solution set is (5,2).

(ii) 3x + 2y = 4; 9x + 6y – 12 = 0
Solution:
2y = -3x + 4
y = \(\frac{-3x+4}{2}\)
= \(\frac{-3}{2}\)x + 2

Plot the points (-2, 5), (0, 2) and (2, -1) in the graph sheet
9x + 6y= 12 (÷3)
3x + 2y = 4
2y = \(\frac{-3x+4}{2}\)
= \(\frac{-3}{2}\)x + 2

Plot the points (-2, 5), (0, 2) and (2, -1) the same graph sheet

Here both the equations are identical, but in different form.
Their solution is same.
This equations have an infinite number of solution.

(iii) \(\frac{x}{2}\) + \(\frac{y}{4}\) = 1: \(\frac{x}{2}\) + \(\frac{y}{4}\) = 2
Solution:
\(\frac{x}{2}\) + \(\frac{y}{4}\) = 1
multiply by 4
2x + y = 4
y = -2x + 4

Plot the points (-3, 10), (-1, 6), (0, 4) and (2, 0) in the graph sheet
\(\frac{x}{2}\) + \(\frac{y}{4}\) = 2
multiply by 4
2x + y = 8
y = -2x + 8

Plot the points (-2, 12), (-1, 10), (0, 8) and (2, 4) in the same graph sheet.

The given two lines are parallel.
∴ They do not intersect a point.
∴ There is no solution.

(iv) x – y = 0; y + 3 = 0
Solution:
x – y = 0
-y = -x
y = x

Plot the points (-2, -2), (0, 0), (1, 1) and (3, 3) in the same graph sheet.
y + 3 = 0
y = -3

Plot the points (-2, -3), (0, -3), (1, -3) and (2, -3) in the same graph sheet.

The two lines l₁ and l₂ intersect at (-3, -3). The solution set is (-3, -3).

(v) y = 2x + 1; 3x – 6 = 0
Solution:
y = 2x + 1

Plot the points (-3, -5), (-1, -1), (0, 1) and (2, 5) in the graph sheet
3x – 6 = 0
y = -3x + 6

Plot the points (-2, 12), (-1, 9), (0, 6) and (2, 0) in the same graph sheet

The two lines l₁ and l₂ intersect at (1, 3).
∴ The solution set is (1, 3).

(vi) x = -3; y = 3
Solution:
x = -3

Plot the points (-3, -3), (-3, -2), (-3, 2) and (-3, 3) in the graph sheet
y = 3

Plot the points (-3, 3), (-1, 3), (0, 3) and (2, 3) in the same graph sheet

The two lines l₁ and l₂ intersect at (-3, 3)
∴ The solution set is (-3, 3)

Question 3.
Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.
Solution:
Let the speed of the two cars be “x” and “y”.
By the given first condition

x+ y = 100 → (1)
(They travel in opposite direction)
By the given second condition.
\(\)\frac{100}{x-y}= 2 [time taken in 2 hours in the same direction]
2x – 2y = 100
x – y = 50 → (2)
x + y = 100
y = 100 – x

Plot the points (30, 70), (50, 50), (60, 40) and (70,30) in the graph sheet
x – y = 50
-y = -x + 50
y = x – 50

Plot the points (40, -10), (50, 0), (60, 10) and (70, 20) in the same graph sheet

The two cars intersect at (75, 25)
The speed of the first car 75 km/hr
The speed of the second car 25 km/hr