Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 Inverse Trigonometric Functions Ex 4.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.6
Choose the most suitable answer from the given four alternatives:
Question 1.
The value of sin-1(cos x), 0 ≤ x ≤ π is
(a) π – x
(b) x – \(\frac {π}{2}\)
(c) \(\frac {π}{2}\) – x
(d) x – π
Solution:
(c) \(\frac {π}{2}\) – x
Hint:
sin-1(cos x) = sin-1(sin(\(\frac {π}{2}\) – x)) = \(\frac {π}{2}\) – x
Question 2.
If sin-1 x + sin-1 y = \(\frac {2π}{3}\); then cos-1 x + cos-1 y is equal to
(a) \(\frac {2π}{3}\)
(b) \(\frac {π}{3}\)
(c) \(\frac {π}{6}\)
(d) π
Solution:
(b) \(\frac {π}{3}\)
Hint:
sin-1x + cos-1x + cos-1y + sin-1y = \(\frac {π}{2}\) + \(\frac {π}{2}\) = π
\(\frac {2π}{3}\) + cos-1x + cos-1y = π
cos-1x + cos-1y = π – \(\frac {2π}{3}\) = \(\frac {3π-2π}{3}\) = \(\frac {π}{3}\)
![]()
Question 3.
sin-1\(\frac {3}{5}\) – cos-1\(\frac {12}{13}\) + sec-1\(\frac {5}{3}\) – cosec-1\(\frac {13}{12}\) is equal to
(a) 2π
(b) π
(c) 0
(d) tan-1\(\frac {12}{65}\)
Solution:
(c) 0
Hint:

Question 4.
If sin-1 x = 2sin-1 α has a solution, then
(a) |α| ≤ \(\frac {1}{√2}\)
(b) |α| ≥ \(\frac {1}{√2}\)
(c) |α| < \(\frac {1}{√2}\)
(d) |α| > \(\frac {1}{√2}\)
Solution:
(a) |α| ≤ \(\frac {1}{√2}\)
Hint:
If sin-1 x = 2sin-1 α has a solution then
–\(\frac {π}{2}\) ≤ 2sin-1α ≤ \(\frac {π}{2}\)
–\(\frac {π}{4}\) ≤ sin-1α ≤ \(\frac {π}{4}\)
sin(\(\frac {-π}{4}\)) ≤ α ≤ sin\(\frac {π}{4}\)
–\(\frac {1}{√2}\) ≤ α ≤ \(\frac {1}{√2}\)
-|α| ≤ \(\frac {1}{√2}\)
![]()
Question 5.
sin-1(cos x) = \(\frac {π}{2}\) – x is valid for
(a) -π ≤ x ≤ 0
(b) 0 ≤ x ≤ π
(c) –\(\frac {π}{2}\) ≤ x ≤ \(\frac {π}{2}\)
(d) –\(\frac {π}{4}\) ≤ x ≤ \(\frac {3π}{4}\)
Solution:
(b) 0 ≤ x ≤ π
Hint:
sin-1 (cosx) = \(\frac {π}{2}\) – x is valid for
cos x = sin (\(\frac {π}{2}\) – x)
cos x ∈ [0, π]
∴ 0 ≤ x ≤ π
Question 6.
If sin-1 x + sin-1 y + sin-1 z = \(\frac {3π}{2}\), the value of show that x2017 + y2018 + z2019 – \(\frac {9}{x^{101}+y^{101}+z^{101}}\) is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:
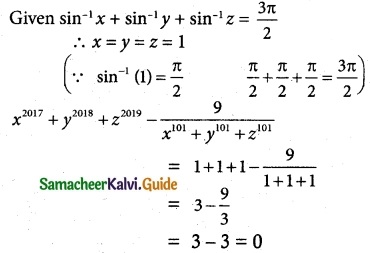
![]()
Question 7.
If cot-1 x = \(\frac {2π}{5}\) for some x ∈ R, the value of tan-1 x is
(a) –\(\frac {π}{10}\)
(b) \(\frac {π}{5}\)
(c) \(\frac {π}{10}\)
(d) –\(\frac {π}{5}\)
Solution:
(c) \(\frac {π}{10}\)
Hint:
tan-1 x + cos-1 \(\frac {π}{2}\)
tan-1x = \(\frac {π}{2}\) – cot-1 x = \(\frac {π}{2}\) – \(\frac {2π}{5}\)
= \(\frac {5π-4π}{10}\) = \(\frac {π}{10}\)
Question 8.
The domain of the function defined by f(x) = sin-1 \(\sqrt {x-1}\) is
(a) [1, 2]
(b) [-1, 1]
(c) [0, 1]
(d) [-1, 0]
Solution:
(a) [1, 2]
Hint:
f(x) = sin-1 \(\sqrt {x-1}\)
\(\sqrt {x-1}\) ≥ 0
-1 ≤ \(\sqrt {x-1}\) ≤ 1
∴ 0 ≤ \(\sqrt {x-1}\) ≤ 1
0 ≤ x – 1 ≤ 1
1 ≤ x ≤ 2
x ∈ [1, 2]
![]()
Question 9.
If x = \(\frac {1}{5}\) the value of cos(cos-1x + 2sin-1x) is
(a) –\(\sqrt{\frac {24}{25}}\)
(b) \(\sqrt{\frac {24}{25}}\)
(c) \(\frac {1}{5}\)
(d) –\(\frac {1}{5}\)
Solution:
(d) –\(\frac {1}{5}\)
Hint:
cos[cos-1x + sin-1x + sin-1x] = cos(\(\frac {π}{2}\) + sin-1x)
= -sin(sin-1x)
[∵ cos(90+θ) = -sin θ]
= -x = –\(\frac {1}{5}\)
Question 10.
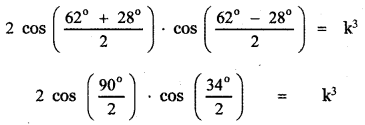
tan-1(\(\frac {1}{4}\)) + tan-1(\(\frac {2}{9}\)) is equal to
(a) \(\frac {1}{2}\)cos-1(\(\frac {3}{5}\))
(b) \(\frac {1}{2}\)sins-1(\(\frac {3}{5}\))
(c) \(\frac {1}{2}\)tan-1(\(\frac {3}{5}\))
(d) tan-1(\(\frac {1}{2}\))
Solution:
(d) tan-1(\(\frac {1}{2}\))
Hint:

![]()
Question 11.
If the function f(x) = sin-1(x² – 3), then x belongs to
(a) [-1, 1]
(b) [√2, 2]
(c) [-2, -√2]∪[√2, 2]
(d) [-2, -√2]
Solution:
(c) [-2, -√2]∪[√2, 2]
Hint:
-1 ≤ x² – 3 ≤ 1
-1 + 3 ≤ x² ≤ 1 + 3
⇒ 2 ≤ x² ≤ 4
±√2 ≤ x ≤ ± 2
[-2, -√2]∪[√2, 2]
Question 12.
If cot-1 2 and cot-1 3 are two angles of a triangle, then the third angle is
(a) \(\frac {π}{4}\)
(b) \(\frac {3π}{4}\)
(c) \(\frac {π}{6}\)
(d) \(\frac {π}{3}\)
Solution:
(b) \(\frac {3π}{4}\)
Hint:
A + B + C = π (triangle)
cot-1 2 + cot-1 3 + C = π

![]()
Question 13.
sin-1(tan\(\frac {π}{4}\)) – sin-1(\(\sqrt{\frac {3}{x}}\)) = \(\frac {π}{6}\). Then x is root of the equation
(a) x² – x – 6 = 0
(b) x² – x – 12 = 0
(c) x² + x – 12 = 0
(d) x² + x – 6 = 0
Solution:
(b) x² – x – 12 = 0
Hint:

Question 14.
sin-1(2 cos²x – 1) + cos-1(1 – 2 sin²x) =
(a) \(\frac {π}{2}\)
(b) \(\frac {π}{3}\)
(c) \(\frac {π}{4}\)
(d) \(\frac {π}{6}\)
Solution:
(a) \(\frac {π}{2}\)
Hint:
sin-1(2 cos² x – 1) + cos-1(1 – 2 sin²x)
= sin-1 (2 cos² x – 1) + cos-1 (1 – sin² x – sin² x)
= sin-1(2 cos² x – 1) + cos-1(cos² x – (1 – cos²x))
= sin-1(2 cos² x – 1) + cos-1(cos² x – 1 + cos²x)
= sin-1(2 cos² x – 1) + cos-1(2 cos² x – 1)
= \(\frac {π}{2}\) [∵ sin-1 x + cos-1 x = \(\frac {π}{2}\)]
![]()
Question 15.
If cot-1(\(\sqrt {sinα}\)) + tan-1(\(\sqrt {sinα}\)) = u, then cos 2u is equal to
(a) tan²α
(b) 0
(c) -1
(d) tan 2α
Solution:
(c) -1
Hint:
cot-1 x + tan-1 x = \(\frac {π}{2}\)
∴ u = \(\frac {π}{2}\)
cos 2u = cos 2(\(\frac {π}{2}\)) = cos π = -1
Question 16.
If |x| ≤ 1, then 2 tan-1 x – sin-1\(\frac {2x}{1+x²}\) is equal to
(a) tan-1x
(b) sin-1x
(c) 0
(d) π
Solution:
(c) 0
Hint:
sin-1\(\frac {2x}{1+x²}\) = 2 tan-1x
∴ 2 tan-1 x – 2 tan-1 x = 0
![]()
Question 17.
The equation tan-1 x – cot-1 x = tan-1(\(\frac {1}{√3}\)) has
(a) no solution
(b) unique solution
(c) two solutions
(d) infinite number of solutions
Solution:
(b) unique solution
Hint:
tan-1 x – cot-1 x = tan-1(\(\frac {1}{√3}\)) …….. (1)
tan-1 x – cot-1 x = \(\frac {π}{2}\) ……… (2)
Add 1 and 2
2 tan-1 x = \(\frac {π}{6}\) + \(\frac {π}{2}\) = \(\frac {2π}{3}\)
tan-1 x = \(\frac {π}{3}\)
x = √3 which is uniqe solution.
Question 18.
If sin-1 x + cot-1(\(\frac {1}{2}\)) = \(\frac {π}{2}\), then x is equal to
(a) \(\frac {1}{2}\)
(b) \(\frac {1}{√5}\)
(c) \(\frac {2}{√5}\)
(d) \(\frac {√3}{2}\)
Solution:
(b) \(\frac {1}{√5}\)
Hint:
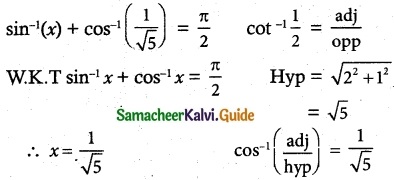
![]()
Question 19.
If sin-1 \(\frac {x}{5}\) + cosec-1\(\frac {5}{4}\) = \(\frac {π}{2}\), then the value of x is
(a) 4
(b) 5
(c) 2
(d) 3
Solution:
(d) 3
Hint:

Question 20.
sin(tan-1 x), |x| < 1 is equal to
(a) \(\frac {x}{\sqrt{1-x^2}}\)
(b) \(\frac {1}{\sqrt{1-x^2}}\)
(c) \(\frac {1}{\sqrt{1+x^2}}\)
(d) \(\frac {x}{\sqrt{1+x^2}}\)
Solution:
(d) \(\frac {x}{\sqrt{1+x^2}}\)
Hint:
tan a = x
W.K.T 1 + tan² a = sec² a
1 + x² = sec² a
sec a = \(\sqrt{1+x^2}\)
\(\frac {1}{cosa}\) = \(\sqrt{1+x^2}\)
cos a= \(\frac {1}{\sqrt{1+x^2}}\)
sin a = \(\sqrt{1-cos^2a}\) = \(\sqrt{1-\frac {1}{1+x^2}}\)
\(\sqrt{\frac{1+x^2 -1}{1+x^2}}\) = \(\frac {x}{\sqrt{1+x^2}}\)
![]()
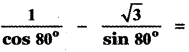







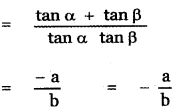

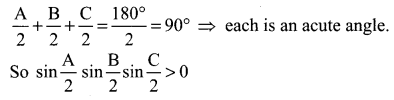


















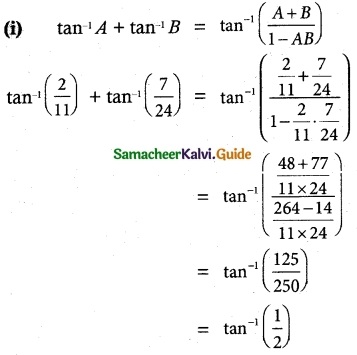

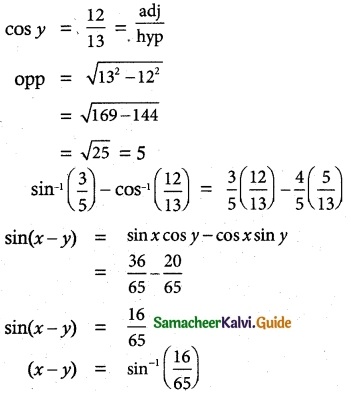


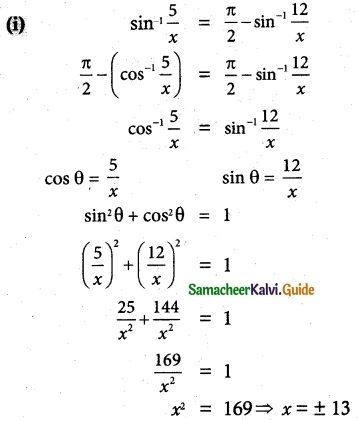


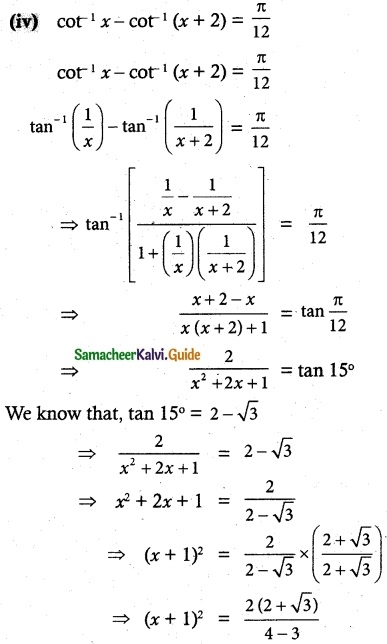


















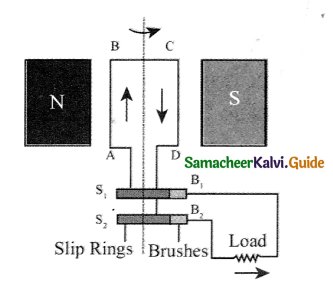
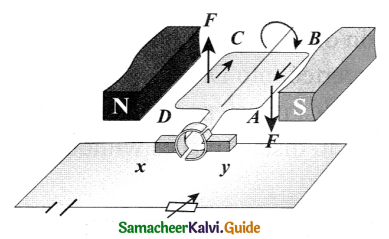
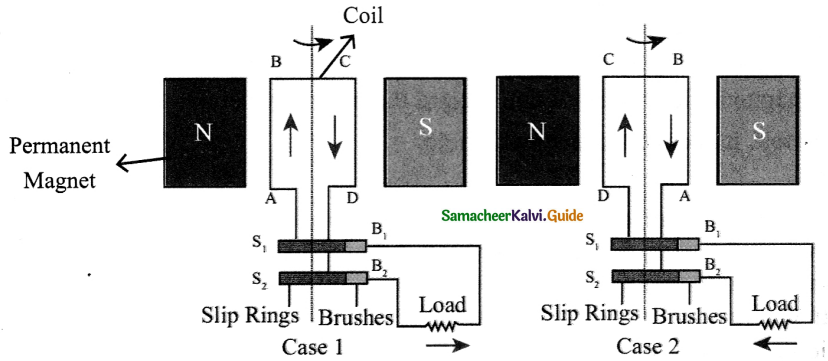
 When the coil is rotated, the magnetic flux linked with the coil changes. This change in magnetic flux will lead to generation of induced current.
When the coil is rotated, the magnetic flux linked with the coil changes. This change in magnetic flux will lead to generation of induced current.