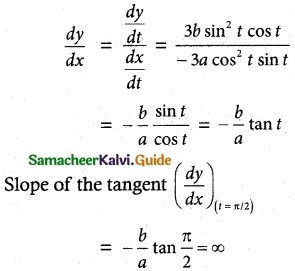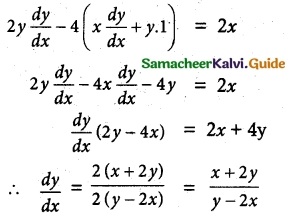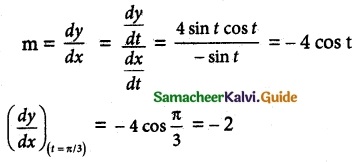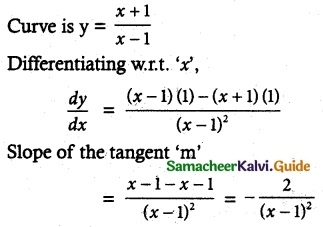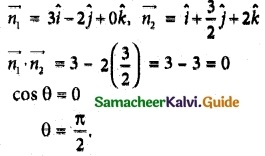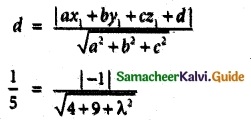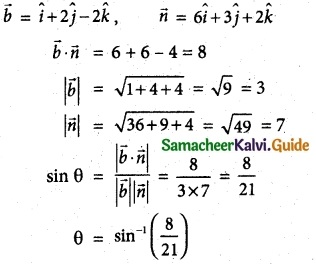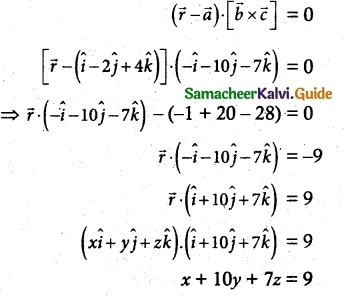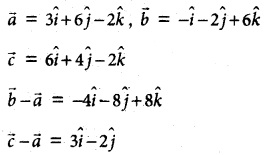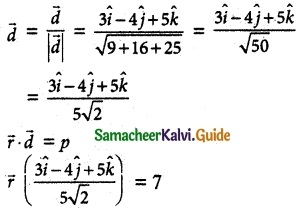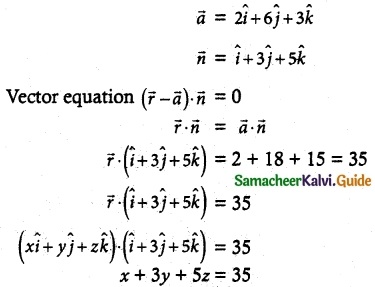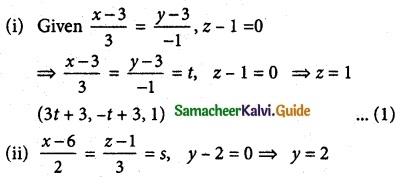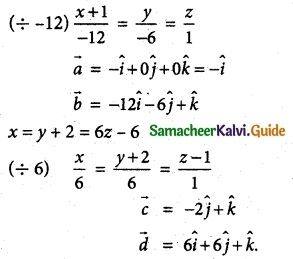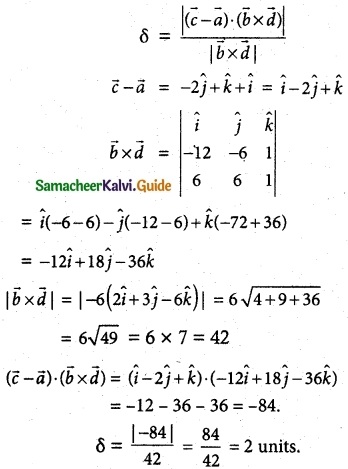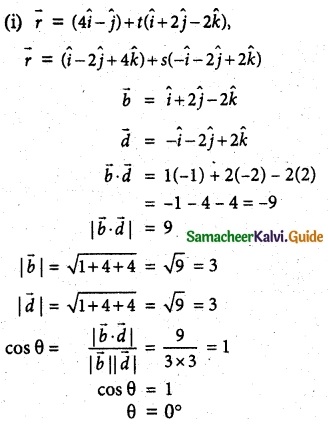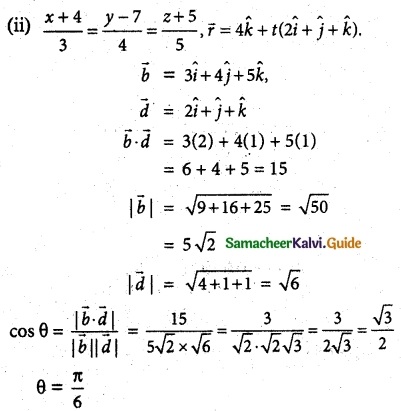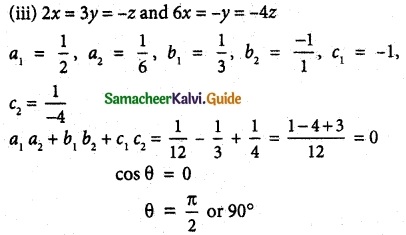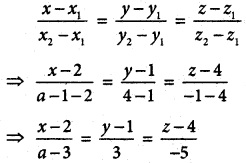Bhagya

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.3

Question 1.
Explain why Rolle’s theorem is not applicable to the following functions in the respective intervals.
(i) f(x) = |\(\frac { 1 }{ x }\)|, x ∈ [-1, 1]
(ii) f(x) = tan x, x ∈ [0, π]
(iii) f(x) = x – 2 log x, x ∈ [2, 7]
Solution:
(i) f(x) = |\(\frac { 1 }{ x }\)|, x ∈ [-1, 1]
f(-1) = 1
f(1) = 1
⇒ f(-1) = f(1) = 1
But f(x) is not differentiable at x = 0
∴ Rolle’s theorem is not applicable.

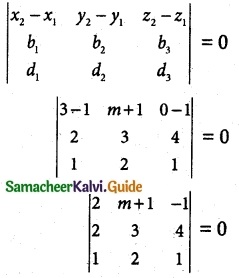
(ii) f (x) = tan x
f(x) is not continuous at x = \(\frac{\pi}{2}\).
So Rolle’s Theorem is not applicable.

(iii) f(x) = x – 2 log x
f(x) = x – 2 log x
f(2) = 2 – 2 log 2 = 2 – log 4
f(7) = 7 – 2 log 7 = 7 – log 49
f(2) ≠ f(7)
So Rolle’s theorem is not applicable.

Question 2.
Using the Rolle’s theorem, determine the values of x at which the tangent is parallel to the x-axis for the following functions:
(i) f(x) = x² – x, x ∈ [0, 1]
(ii) f(x) = \(\frac { x^2-2x }{ x+2 }\), x ∈ [-1, 6]
(iii) f(x) = √x – \(\frac { x }{ 3 }\), x ∈ [0, 9]
Solution:
(i) f(x) = x² – x, x ∈ [0, 1]
f(0) = 0, f(1) = 0
⇒ f(0) = f(1) = 0
f(x) is continuous on [0, 1]
f(x) is differentiable on (0, 1)
Now, f'(x) = 2x – 1
Since, the tangent is parallel to x-axis then
f'(x) = 0 ⇒ 2x – 1 = 0
x = \(\frac { x }{ 3 }\) ∈ (0, 1)

(ii) f(x) = \(\frac { x^2-2x }{ x+2 }\), x ∈ [-1, 6]
f(-1) = \(\frac { 1+2 }{ -1+2 }\) = 3
f(6) = \(\frac { 36-12 }{ 8 }\) = \(\frac { 24 }{ 8 }\) = 3
⇒ f (-1) = 3 = f(6)
f(x) is continuous on [- 1, 6]
f(x) is differentiable on (- 1, 6)
Now, f'(x)

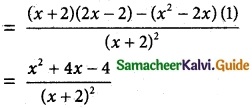
Since the tangent is parallel to the x-axis.
f'(x) = 0
⇒ x² + 4x – 4 = 0
⇒ x = –\(\frac { 4±\sqrt{16+16} }{ 2 }\)
x = –\(\frac { 4±4√2 }{ 2 }\) = -2 ± 2√2
x = -2 ± 2√2 ∈ (-1, 6)

(iii) f(x) = √x – \(\frac { x }{ 3 }\), x ∈ [0, 9]
f(0) = 0, f(9) = √9 – \(\frac { 9 }{ 3 }\) = 3 – 3 = 0
⇒ f(0) = 0 = f(9)
f(x) is continuous on [0, 9]
f(x) is differentiable on (0, 9)
Now f'(x) = \(\frac { 1 }{ 2√x }\) – \(\frac { 1 }{ 3 }\)
Since, the tangent is parallel to x-axis.
f'(x) = 0

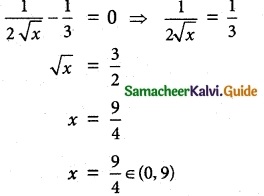
Question 3.
Explain why Lagrange’s mean value theorem is not applicable to the following functions in the respective intervals:
(i) f(x) = \(\frac { 1 }{ 2√x }\), x ∈ [-1, 2]
(ii) f(x) = |3x + 1|, x ∈ [-1, 3]
Solution:
(i) f(x) = \(\frac { 1 }{ 2√x }\), x ∈ [-1, 2]
f(0) = undefined
∴ f(x) is not continuous at x = 0
Hence, Lagrange’s mean value theorem is not applicable.

(ii) f(x) =|3x + 1|, x ∈ [-1, 3]
The function is not differentiable at x = \(\frac{-1}{3}\).
So Lagrange’s mean value theorem is not applicable in the given interval.

Question 4.
Using the Lagrange’s mean value theorem determine the values of x at which the tangent is parallel to the secant line at the end points of the given interval:
(i) f(x) = x³ – 3x + 2, x ∈ [-2, 2]
(ii) f(x) = (x – 2) (x – 7), x ∈ [3, 11]
Solution:
f(x) = x³ – 3x + 2, x ∈ [-2, 2]
f(x) is continuous in [- 2, 2]
f(x) is differentiable in (- 2, 2)
f(-2) = (-2)³ – 3 (-2) + 2 = – 8 + 6 + 2 = 0
f(2) = (2)³ -3(2) + 2 = 8 – 6 + 2 = 4
∴ f(x) is defined in the given interval.
Given that tangent is parallel to the secant line of the curve between x = -2 and x = 2.

(ii) f(x) = (x – 2)(x – 7), x ∈ [3, 11]
f(x) is continuous in [3, 11]
f(x) is differentiable in (3, 11)
f(3) = (3 – 2) (3 – 7) = (1) (-4) = -4
f(11) = (11 – 2) (11 – 7) = (9) (4) = 36
∴ f(x) is defined in the given interval.
Given that the tangent is parallel to the secant line ofthe curve between x = 3 and x = 11.
∴ f'(c) = \(\frac { f(b)-f(a) }{ b-a }\)
2c – 9 = \(\frac { 36+4 }{ 11-3 }\) where f'(x) = 2x – 9
2x – 9 = \(\frac { 40 }{ 8 }\) = 5
2c = 14 ⇒ c = 7 ∈ (3, 11)
∴ x = 7.

Question 5.
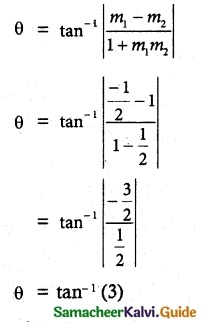
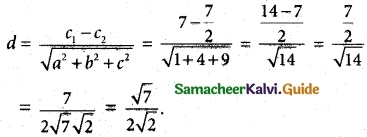
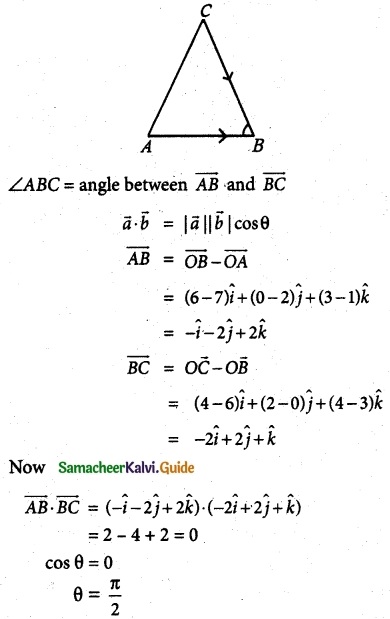
Show that the value in the conclusion of the mean value theorem for
(i) f(x) = \(\frac { 1 }{ x }\) on a closed interval of positive numbers [a, b] is \(\sqrt { ab }\)
(ii) f(x) = Ax² + Bx + C on any interval [a, b] is \(\frac { a+b }{ 2 }\)
Solution:

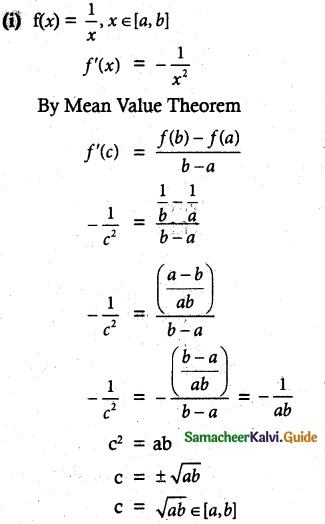
(ii) f(x) = Ax² + Bx + C, x ∈ [a, b]
f'(x) = 2Ax + B
By Mean Value Theorem,

Question 6.
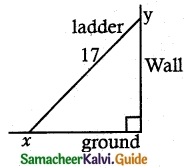
A race car driver is racing at 20th km. If his speed never exceeds 150 km/hr, what is the maximum distance he can cover in the next two hours?
Solution:
Let a = 0, b = 2 and the interval is [0, 2] and f(0) = 20 (given)
We need to find f(2)
By Lagrange’s Mean Value Theorem,
f(b) – f(a) ≤ f'(c) [b – a]
f(b) – 20 ≤ 150(2 – 0)
f(b) ≤ 300 + 20
f(b) ≤ 320
∴ Maximum distance f(2) = 320 km.

Question 7.
Suppose that for a function f(x), f'(x) ≤ 1 for all 1 ≤ x ≤ 4. Show that f(4) – f(1) ≤ 3.
Solution:
Given: For f(x), f'(x) ≤ 1 for all 1 ≤ x ≤ 4
∴ a = 1, b = 4.
By Lagrange’s Mean Value Theorem,
f(b) – f(a) ≤ f'(c) (b – a)
f(4) – f(1) ≤ 1(4 – 1)
f(4) – f(1) ≤ 3
Hence Proved.

Question 8.
Does there exist a differentiable function f(x) such that f(0) = -1, f(2) = 4 and f (x) ≤ 2 for all x. Justify your answer.
Solution:
Given:For f(x), f'(x) ≤ 2, f(0) = -1, f(2) = 4
∴ a = 0, b = 2
By Lagrange’s Mean Value Theorem,
f(b) – f(a) ≤ f'(c)(b – a)
f(2) – f(0) ≤ f'(c) (2 – 0)
\(\frac { 4+1 }{ 2 }\) ≤ f'(c) ⇒ \(\frac { 5 }{ 2 }\) ≤ f'(c) ≤ 2 (given)
f(x) cannot be a differentiable function in (0, 2) as f'(x) cannot be 2.5.

Question 9.
Show that there lies a point on the curve f(x) = x(x + 3)e^-π/2, -3 ≤ x ≤ 0 where tangent drawn is parallel to the x-axis.
Solution:
f(x) = x(x + 3)e^-π/2, -3 ≤ x ≤ 0
f(x) is continuous in [-3, 0]
f(x) is differentiable in (- 3, 0)
f(-3) = -3 (-3 + 3)e^-π/2 = 0
f(0) = 0
⇒ f(-3) = f(0) = 0
Since the tangent is parallel to x-axis.
f'(c) = 0
e^-π/2 (2c + 3) = 0 where f'(x) = e^-π/2 (2x + 3)
2c + 3 = 0
c = –\(\frac { 3 }{ 2 }\) ∈ (-3, 0)
∴ The point lies on the curve.

Question 10.
Using Mean Value Theorem prove that for, a > 0, b > 0, |e^-a – e^-b| < |a – b|
Solution:
Let f(x) = e^-x
f'(x) = e^-x
By Lagrange’s Mean Value Theorem,

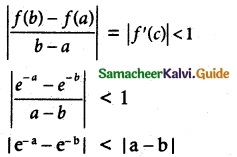
Hence Proved.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.2

Question 1.
Find the slope of the tangent to the following curves at the respective given points.
(i) y = x⁴ + 2x² – x at x = 1
(ii) x = a cos³ t, y = b sin³ t at t = \(\frac { π }{ 2 }\)
Solution:
(i) y = x⁴ + 2x² – x
Differentiating w.r.t. ‘x’
\(\frac { dy }{ dx }\) = 4x³ + 4x – 1
Slope of the tangent (\(\frac { dy }{ dx }\))_(x=1)
= 4(1)³ + 4(1) – 1
= 4 + 4 – 1 = 7
(ii) x = a cos³ t, y = b sin³ t
Differenriating w.r.t. ‘t’
\(\frac { dx }{ dt }\) = – 3a cos² t sin t
\(\frac { dy }{ dt }\) = 3b sin² t sin t

Question 2.
Find the point on the curve y = x² – 5x + 4 at which the tangent is parallel to the line 3x + y = 7.
Solution:
y = x² – 5x + 4
Differentiating w.r.t. ‘x’
Slope of the tangent \(\frac { dy }{ dx }\) = 2x – 5
Given line 3x + y = 7
Slope of the line = –\(\frac { 3 }{ 1 }\) = -3
Since the tangent is parallel to the line, their slopes are equal.
∴ \(\frac { dy }{ dx }\) = -3
⇒ 2x – 5 = -3
2x = 2
x = 1
When x = 1, y = (1)² – 5 (1) + 4 = 0
∴ Point on the curve is (1, 0).

Question 3.
Find the points on curve y = x³ – 6x² + x + 3 where the normal is parallel to the line x + y = 1729.
Solution:
y = x³ – 6x² + x+ 3
Differentiating w.r.t. ‘x’
Slope of the tangent \(\frac { dy }{ dx }\) = 3x² – 12x + 1
Slope of the normal = \(\frac { 1 }{ 3x^2 – 12x + 1 }\)
Given line is x + y = 1729
Slope of the line is – 1
Since the normal is parallel to the line, their slopes are equal.
\(\frac { 1 }{ 3x^2 – 12x + 1 }\) = -1
3x² – 12x + 1 = 1
3x² – 12x =0
3x(x – 4) = 0
x = 0, 4
When x = 0, y = (0)³ – 6(0)² + 0 + 3 = 3
When x = 4, y = (4)³ – 6(4)² + 4 + 3
= 64 – 96 + 4 + 3 = -25
∴ The points on the curve are (0, 3) and (4, -25).

Question 4.
Find the points on the curve y² – 4xy = x² + 5 for which the tangent is horizontal.
Solution:
y² – 4xy = x² + 5 ………… (1)
Differentiating w.r.t. ‘x’

When the tangent is horizontal(Parallel to X-axis) then slope of the tangent is zero.
\(\frac { dy }{ dx }\) = 0 ⇒ \(\frac { x+2y }{ y-2x }\) = 0
⇒ x + 2y = 0
x = -2y
Substituting in (1)
y² – 4 (-2y) y = (-2y)² + 5
y² + 8y² = 4y² + 5
5y² = 5 ⇒ y² = 1
y = ±1
When y = 1, x = -2
When y = – 1, x = 2
∴ The points on the curve are (- 2, 1) and (2, -1).

Question 5.
Find the tangent and normal to the following curves at the given points on the curve.
(i) y = x² – x⁴ at (1, 0)
(ii) y = x⁴ + 2e^x at (0, 2)
(iii) y = x sin x at (\(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\))
(iv) x = cos t, y = 2 sin² t at t = \(\frac { π }{ 3 }\)
Solution:
(i) y = x² – x⁴ at (1, 0)
Differentiating w.r.t. ‘x’
\(\frac { dx }{ dy }\) = 2x – 4x³
Slope of the tangent ‘m’ = (\(\frac { dx }{ dy }\))_{(1, 0)}
= 2 (1) – 4 (1)³ = -2
Slope of the normal –\(\frac { 1 }{ m }\) = \(\frac { -1 }{ -2 }\) = \(\frac { 1 }{ 2 }\)
Equation of tangent is
y – y₁ = m (x – x₁)
y – 0 = – 2 (x – 1)
y = -2x + 2
2x + y – 2 = 0
Equation of Normal is
y – y₁ = –\(\frac { 1 }{ m }\)(x – x₁)
y – 0 = \(\frac { 1 }{ 2 }\)(x – 1)
2y = x- 1
x – 2y – 1 = 0

(ii) y = x⁴ + 2e^x at (0, 2)
Differentiating w.r.t. ‘x’
\(\frac { dy }{ dx }\) = 4x³ + 2e^x
Slope of the tangent ‘m’
(\(\frac { dy }{ dx }\))_{(0, 2)} = 4(0)³ + 2e⁰ = 2
Slope of the Normal –\(\frac { 1 }{ m }\) =-\(\frac { 1 }{ 2 }\)
Equation of tangent is
y – y₁ = m(x – x₁)
⇒ y – 2 = 2(x – 0)
⇒ y – 2 = 2x
⇒ 2x – y + 2 = 0
Equation of Normal is
y – y₁ = –\(\frac { 1 }{ m }\) (x – x₁)
y – 2 = –\(\frac { 1 }{ 2 }\)(x – 0)
2y – 4 = -x
x + 2y – 4 = 0

(iii) y = x sin x at (\(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\))
Differentiating w.r.t. ‘x’
\(\frac { dy }{ dx }\) = x cos x + sin x
Slope of the tangent ‘m’ = (\(\frac { dy }{ dx }\))_{(π/2, π/2)}
= \(\frac { π }{ 2 }\) cos \(\frac { π }{ 2 }\) + sin \(\frac { π }{ 2 }\) = 1
Slope of the Normal –\(\frac { 1 }{ m }\) = -1
Equation of tangent is
y – y₁ = m(x – x₁)
⇒ y – \(\frac { π }{ 2 }\) = 1 (x – \(\frac { π }{ 2 }\))
⇒ x – y = 0
Equation of Normal is
y – y₁ = –\(\frac { 1 }{ m }\)(x – x₁)
⇒ y – \(\frac { π }{ 2 }\) = -1(x – \(\frac { π }{ 2 }\))
⇒ y – \(\frac { π }{ 2 }\) = -x + \(\frac { π }{ 2 }\)
⇒ x + y – π = 0

(iv) x = cos t, y = 2 sin² t at t = \(\frac { π }{ 2 }\)
at t = \(\frac { π }{ 3 }\), x = cos \(\frac { π }{ 3 }\) = \(\frac { 1 }{ 2 }\)
at t = \(\frac { π }{ 3 }\), y = 2 sin² \(\frac { π }{ 3 }\) = 2(\(\frac { 3 }{ 4}\)) = \(\frac { 3 }{ 2 }\)
Point is (\(\frac { 1 }{ 2 }\), \(\frac { 3 }{ 2 }\))
Now x = cos t y = 2 sin² t
Differentiating w.r.t. ‘t’,
\(\frac { dx }{ dt }\) = -sin t; \(\frac { dy }{ dt }\) = 4 sin t cos t
Slope of the tangent

Slope of the Normal –\(\frac { 1 }{ m }\) = \(\frac { 1 }{ 2 }\)
Equation of tangent is
y – y₁ = m(x – x₁)
⇒ y – \(\frac { 3 }{ 2 }\) = -2(x – \(\frac { 1 }{ 2 }\))
⇒ 2y – 3 = – 4x + 2
⇒ 4x + 2y – 5 = 0
Equation of Normal is
y – y₁ = –\(\frac { 1 }{ m }\)(x – x₁)
⇒ y – \(\frac { 3 }{ 2 }\) = \(\frac { 1 }{ 2 }\)(x – \(\frac { 1 }{ 2 }\))
⇒ 2 (2y – 3) = 2x – 1
⇒ 4y – 6 = 2x – 1
⇒ 2x – 4y + 5 = 0

Question 6.
Find the equations of the tangents to the curve y = 1 + x³ for which the tangent is orthogonal with the line x + 12y = 12.
Solution:
Curve is y = 1 + x³
Differentiating w.r.t ‘x’,
Slope of the tangent ‘m’ = \(\frac { dy }{ dx }\) = 3x²
Given line is x + 12y = 12
Slope of the line is –\(\frac { 1 }{ 12 }\)
Since the tangent is orthogonal with the line, the slope of the tangent is 12.
∴ \(\frac { dy }{ dx }\) = 12
i.e 3x² = 12
x² = 4
x = ±2
When x = 2, y = 1 + 8 = 9 ⇒ point is (2, 9)
When x = -2, y = 1 – 8 = -7 ⇒ point is (-2, -7)
Equation of tangent with slope 12 and at the j point (2, 9) is
y – 9 = 12 (x – 2)
y – 9 = 12x – 24
12x – y – 15 = 0
Equation of tangent with slope 12 and at the point (-2, -7) is
y + 7 = 12 (x + 2)
y + 7 = 12x + 24
12x – y + 17 = 0

Question 7.
Find the equations of the tangents to the curve y = –\(\frac { x+1 }{ x-1 }\) which are parallel to the line x + 2y = 6.
Solution:

Given line is x + 2y = 6
Slope of the line = –\(\frac { 1 }{ 2 }\)
Since the tangent is parallel to the line, then the slope of the tangent is –\(\frac { 1 }{ 2 }\)
∴ \(\frac { dy }{ dx }\) = \(\frac { 2 }{ (x-1)^2 }\) = –\(\frac { 1 }{ 2 }\)
(x – 1)² = 4
x – 1 = ±2
x = -1, 3
When x = – 1, y = 0 ⇒ point is (-1, 0)
When x = 3, y = 2 ⇒ point is (3, 2)
Equation of tangent with slope –\(\frac { 1 }{ 2 }\) and at the point (-1, 0) is
y – o = –\(\frac { 1 }{ 2 }\)(x + 1)
2y = -x – 1 ⇒ x + 2y + 1 = 0
Equation of tangent with slope –\(\frac { 1 }{ 2 }\) and at the point (3, 2) is 2
y – 2 = –\(\frac { 1 }{ 2 }\) (x – 3)
2y – 4 = -x + 3
x + 2y – 7 = 0.

Question 8.
Find the equation of tangent and normal to the curve given by x – 7 cos t andy = 2 sin t, t ∈ R at any point on the curve.
Solution:
x = 7 cos t and y = 2 sin t, t ∈ R
Differentiating w.r.t. ‘t’,
\(\frac { dx }{ dt }\) = -7 sin t and \(\frac { dy }{ dt }\) = 2 cos t
Slope of the tangent ‘m’
\(\frac { dy }{ dx }\) = \(\frac{\frac { dy }{ dt }}{\frac{ dx }{ dt }}\) = \(\frac { 2 cot t }{ -7 sin t }\)
Any point on the curve is (7 Cos t, 2 sin t)
Equation of tangent is y – y₁ = m (x – x₁)
y – 2 sint = –\(\frac { 2 cot t }{ 7 sin t }\) (x – 7 cos t)
7y sin t – 14 sin² t = -2x cos t + 14 cos² t
2x cos t + 7 y sin t – 14 (sin² t + cos² t) = 0
2x cos t + 7y sin t – 14 = 0
Now slope of normal is –\(\frac { 1 }{ 3 }\) = \(\frac { 7 sin t }{ 2 cos t }\)
Equation of normal is y – y₁ = –\(\frac { 1 }{ m }\)(x – x₁)
y – 2 sin t = \(\frac { 7 sin t }{ 2 cos t }\) (x – 7 cos t)
2y cos t – 4 sin t cos t = 7x sin t – 49 sin t cos t 7x sin t – 2y cos t – 45 sin t cos t = 0

Question 9.
Find the angle between the rectangular hyperbola xy = 2 and the parabola x² + 4y = 0
Solution:
Given curves are xy = 2 ……… (1)
x² + 4y = 0 ………. (2)
Now solving (1) and (2)
Substituting (1) in (2)
⇒ x² + 4(2/x) = 0
x³ + 8 = 0
x³ = -8
x = -2
Substituting in (1) ⇒ y = \(\frac { 2 }{ -2 }\) = -1
∴ Point of intersection of (1) and (2) is (-2, -1)
xy = 2 ⇒ y = \(\frac { 2 }{ x }\) ……….. (1)
Differentiating w.r.t. ‘x’

The angle between the curves

Question 10.
Show that the two curves x² – y² = r² and xy = c² where c, r are constants, cut orthogonally.
Solution:
Given curves are x² – y² = r² ……….. (1)
xy = c² …….. (2)
Let (x₁, y₁) be the point of intersection of the given curves.
(1) ⇒ x² – y² = r²
Differentiating w.r.t ‘x’,
2x – 2y \(\frac { dx }{ dy }\) = 0
\(\frac { dx }{ dy }\) = \(\frac { x }{ y }\)
now (\(\frac { dx }{ dy }\))(_x1,y1) = m₁ = \(\frac { x_1 }{ y_1 }\)
(2) ⇒ xy = c²
Differentiating w.r.t ‘x’,

Hence, the given curves cut orthogonally.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.1

Question 1.
A particle moves along a straight line in such a way that after t seconds its distance from the origin is s = 2t² + 3t metres.
(i) Find the average velocity between t = 3 and t = 6 seconds.
(ii) Find the instantaneous velocities at t = 3 and t = 6 seconds.
Solution:
s = 2t² + 3t
(i) Average velocity between t = 3 and t = 6 seconds
Now s(t) = 2t² + 3t
Average velocity

(ii) f(t) = 2t² + 3t
f'(t) = 4t + 3
f'(3) = 4(3) + 3 = 15
f'(6) = 4(3) + 3 = 15

Question 2.
A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera falls a distance of s = 16t² in t seconds.
(i) How long does the camera fall before it hits the ground?
(ii) What is the average velocity with which the camera falls during the last 2 seconds?
(iii) What is the instantaneous velocity of the camera when it hits the ground?
Solution:
(i) The camera falls a distance of s = 16t² in t sec.
s = 400 ft
∴ 16t² =400
t² = \(\frac { 400 }{ 16 }\) = 25
t = 5 sec
∴ Camera falls for 5 sec before it hits the ground.

(ii) In 5 sec camera falls 400 ft (given)
∴ Average velocity in 2 sec
= \(\frac { s(5)-s(3) }{ 5-3 }\)
= \(\frac { 16(5^2)-16(3^2) }{ 2 }\)
= \(\frac { 400-144 }{ 2 }\)
= \(\frac { 256 }{ 2 }\)
= 128 ft/sec

(iii) f(t) = 16t²
f'(t) = 32t
f'(t) at t = 5 = 32(5)
= 160 ft/sec

Question 3.
A particle moves along a line according to the law s(t) = 2t³ – 9t² + 12t – 4, where t ≥ 0.
(i) At what times the particle changes direction?
(ii) Find the total distance travelled by the particle in the first 4 seconds.
(iii) Find the particle’s acceleration each time the velocity is zero.
Solution:
s (t) = 2t³ – 9t² + 12t – 4, t ≥ 0
velocity v = \(\frac { ds }{ dt }\) = 6t² – 18t + 12
When the particle changes its direction, v = 0
6t² – 18t + 12 = 0 (÷6)
t² – 3t + 2 = 0
(t – 2) (t – 1) = 0
t = 1, 2
∴ When time t = 1 sec and t = 2 sec, the particle changes its direction.

(ii) The distance travelled in the first 4 seconds is
|s(0) – s(1)| + |s(1) – s(2)| + |s(2) – s(3)| + |s(3) – s(4)|
Here, s(t) = 2t³ – 9t² + 12t – 4
s(0) = -4
s(1) = 1
s(2) = 0
s(3) = 5
and s(4) = 28
∴ Distance travelled in the first 4 seconds
= |-4 – 1| + |1 – 0| + |0 – 5| + |5 – 28|
= 5 + 1 + 5 + 23 = 34 m

(iii) s (t) = 2t³ – 9t² + 12t – 4
velocity v = \(\frac { ds }{ dt }\) = 6t² – 18t + 12
v = 0 ⇒ 6(t² – 3t + 2) = 0 ⇒ t = 1, 2
Acceleration = \(\frac { d^2s }{ dt^2 }\) = 12t – 18
at t = 1, Acceleration = 12(1) – 18 = -6m/sec²
at t = 2, Acceleration = 12 (2) – 18 = 6 m/sec²

Question 4.
If the volume of a cube of side length x is v = x³. Find the rate of change of the volume with respect to x when x = 5 units.
Solution:
volume of a cube v = x³
Rate of change \(\frac { dv }{ dx }\) = 3x²
When x = 5 units, \(\frac { dv }{ dx }\) = 3(5)² = 3(25) = 75 units.

Question 5.
If the mass m(x) (in kilograms) of a thin rod of length x (in metres) is given by, m(x) = \(\sqrt { 3x }\) then what is the rate of change of mass with respect to the length when it is x = 3 and x = 27 metres.
Solution:

Question 6.
A stone is dropped into a pond causing ripples in the from of concentric circles. The radius r of the outer ripple is increasing at a constant rate of 2 cm per second. When the radius is 5 cm find the rate of changing of the total area of the disturbed water?
Solution:
radius = r, Rate of changes of radius \(\frac { dr }{ dt }\) = 2 and
given r = 5 cm
Area of circle A = πr²
Differentiating w.r.t ‘t’,
\(\frac { dA }{ dt }\)= 2πr\(\frac { dr }{ dt }\)
= 2π (5) (2)
= 20 π
∴ Area of circle (ripple) is increasing at the rate of 20 π cm²/sec.

Question 7.
A beacon makes one revolution every 10 seconds. It is located on a ship which is anchored 5 km from a straight shore line. How fast is the beam moving along the shoreline when it makes an angle of 45° with the shore?
Solution:

Time for one revolution = 10 sec
Now, angular velocity \(\frac { dv }{ dt }\) = \(\frac { 2π }{ 10 }\) = \(\frac { π }{ 5 }\)
From the figure, tan 45° = \(\frac { AB }{ OA }\)
1 = \(\frac { x }{ 5 }\) ⇒ x = 5
Again, tan θ = \(\frac { x }{ 5 }\)
x = 5 tan θ
Differentiating w.r.t. ‘t’
\(\frac { dx }{ dt }\) = 5 sec² θ \(\frac { dθ }{ dt }\)
= 5 sec² (45°) (\(\frac { π }{ 5 }\))
= (√2)² π = 2π
∴ The beam is moving at the rate of 2π km/sec.

Question 8.
A conical water tank with a vertex down of 12 metres height has a radius of 5 metres at the top. If water flows into the tank at a rate of 10 cubic m/min, how fast is the depth of the water increases when the water is 8 metres deep?
Solution:

From the figure \(\frac { r}{ h }\) = \(\frac { 5 }{ 12 }\)
r = \(\frac { 5h }{ 12 }\)
given rate of change of volume \(\frac { dV }{ dt }\) = 10
When h = 8 to find \(\frac { dh }{ dt }\)
Volume of cone V = \(\frac { 1 }{ 3 }\) πr² h

The depth of the water increasing at the rate of \(\frac { 9 }{ 10π }\) m/min

Question 9.
A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5 m/s. When the base of the ladder is 8 metres from the wall.
(i) How fast is the top of the ladder moving down the wall?
(ii) At what rate, the area of the triangle formed by the ladder, wall, and floor is changing?
Solution:

Let the height of the wall where the ladder touches are ‘y’ m.
The bottom of the ladder is at a distance of ‘x’ m from the wall.
Given x = 8, \(\frac { dx }{ dt }\) = 5
x² + y² = 17²
(Pythagoras Theorem)
y² = 17² – x² = 289 – 64 = 225
∴ y = 15
Differentiating w.r.t. ‘t’

(i) The top of the ladder is moving down the wall at the rate of \(\frac { 8 }{ 3 }\) m/sec
(ii) Area of triangle formed by the ladder, wall and the floor is A = \(\frac { 1 }{ 2 }\) xy
differentiating w.r.t. ‘t’

∴ Area of the triangle is increasing at the rate of 26.83 m²/sec.

Question 10.
A police jeep, approaching an orthogonal intersection from the northern direction, is chasing a speeding car that has turned and moving straight east. When the jeep is 0.6 km north of the intersection and the car is 0.8 km to the east. The police determine with a radar that the distance between them and the car is increasing at 20 km/hr. If the jeep is moving at 60 km/hr at the instant of measurement, what is the speed of the car?
Solution:

given x = 0.8, y = 0.6, \(\frac { dy }{ dt }\) = -60
and \(\frac { ds }{ dt }\) = 20
from the figure
S² = x² + y²,
S² = (0.8)² + (0.6)² = 0.64 + 0.36 = 1
S² = 1 ⇒ S = 1
S² = x² + y²,
Differentiating w.r.t. ‘t’

∴ Speed of the car is 70 km/hr.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.10 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.10

Choose the most suitable answer from the given four alternatives

Question 1.
If \(\overline { a }\) and \(\overline { b }\) are parallel vectors, then [\(\overline { a }\), \(\overline { c }\), \(\overline { b }\)] is equal to
(a) 2
(b) -1
(c) 1
(d) 0
Solution:
(d) 0
Hint:
Since \(\overline { a }\) and \(\overline { b }\) are parallel ⇒ \(\overline { a }\) = λ\(\overline { b }\)
[ \(\overline { a }, \overline { c }, \overline { b }\)] = [λ\(\overline { b }, \overline { c }, \overline { b }\) ]
= λ[ \(\overline { b }, \overline { c }, \overline { b }\) ]
= λ(0) = 0

Question 2.
If a vector \(\overline { α }\) lies in the plane of \(\overline { ß }\) and \(\overline { γ }\), then
(a) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 1
(b) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = -1
(c) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 0
(d) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 2
Solution:
(c) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 0
Hint:
If \(\overline { α }\) lies in \(\overline { ß }\) & \(\overline { γ }\) plane
we have [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 0

Question 3.
If \(\overline { a }\).\(\overline { b }\) = \(\overline { b }\).\(\overline { c }\) = \(\overline { c }\).\(\overline { a }\) = 0, then the value of [ \(\overline { a }, \overline { b }, \overline { c }\) ] is
(a) |\(\overline { a }\)| |\(\overline { b }\)| |\(\overline { c }\)|
(b) \(\frac { 1 }{ 3 }\)|\(\overline { a }\)| |\(\overline { b }\)| |\(\overline { c }\)|
(c) 1
(d) -1
Solution:
(a) |\(\overline { a }\)| |\(\overline { b }\)| |\(\overline { c }\)|
Hint:

Question 4.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are three unit vectors such that \(\overline { a }\) is perpendicular to \(\overline { b }\) and is parallel to \(\overline { c }\) then \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) is equal to
(a) \(\overline { a }\)
(b) \(\overline { b }\)
(c) \(\overline { c }\)
(d) \(\overline { 0 }\)
Solution:
(b) \(\overline { b }\)
Hint:

Question 5.
If [ \(\overline { a }, \overline { b }, \overline { c }\) ] = 1 then the value of

(a) 1
(b) -1
(c) 2
(d) 3
Solution:
(a) 1
Hint:

Question 6.
The volume of the parallelepiped with its edges represented by the vectors \(\hat { i }\) + \(\hat { j }\), \(\hat { i }\) + 2\(\hat { j }\), \(\hat { i }\) + \(\hat { j }\) + π\(\hat { k }\) is
(a) \(\frac { π }{ 2 }\)
(b) \(\frac { π }{ 3 }\)
(c) π
(d) \(\frac { π }{ 4 }\)
Solution:
(c) π
Hint:
\(\left|\begin{array}{lll}
1 & 1 & 0 \\
1 & 2 & 0 \\
1 & 1 & \pi
\end{array}\right|\) = π\(\left|\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right|\)
= π (2 – 1) = π

Question 7.
If \(\overline { a }\) and \(\overline { b }\) are unit vectors such that [\(\overline { a }\), \(\overline { b }\), \(\overline { a }\) × \(\overline { b }\)] = \(\frac { 1 }{ 4 }\), then the angle between \(\overline { a }\) and \(\overline { b }\) is
(a) \(\frac { π }{ 6 }\)
(b) \(\frac { π }{ 4 }\)
(c) \(\frac { π }{ 3 }\)
(d) \(\frac { π }{ 2 }\)
Solution:
(a) \(\frac { π }{ 6 }\)
Hint:

Question 8.
If \(\overline { a }\) = \(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\), \(\overline { b }\) = \(\hat { i }\) + \(\hat { j }\), \(\overline { c }\) = \(\hat { i }\) and (\(\overline { a }\) × \(\overline { b }\))\(\overline { c }\) – λ\(\overline { a }\) + µ\(\overline { b }\) then the value of λ + µ is
(a) 0
(b) 1
(c) 6
(d) 3
Solution:
(a) 0
Hint:
\(\overline { a }\).\(\overline { c }\) = 1 and \(\overline { b }\).\(\overline { c }\) = 1
(\(\overline { a }\) × \(\overline { b }\))\(\overline { c }\) = (\(\overline { c }\) × \(\overline { a }\))\(\overline { b }\) – (\(\overline { c }\) × \(\overline { b }\))\(\overline { a }\) = λ\(\overline { a }\) + µ\(\overline { b }\)
⇒ µ = c; a = 1λ = -(\(\overline { c }\).\(\overline { b }\)) = -1
µ + λ = 1 – 1 = 0

Question 9.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are non-coplanar, non-zero vectors
such that [\(\overline { a }\), \(\overline { b }\), \(\overline { c }\)] = 3, then {[\(\overline { a }\) × \(\overline { b }\), \(\overline { b }\) × \(\overline { c }\), \(\overline { c }\) × \(\overline { a }\)]²} is equal to
is equal to
(a) 81
(b) 9
(c) 27
(d) 18
Solution:
(a) 81
Hint:

= 3⁴ = 81

Question 10.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are three non-coplanar vectors such that \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) = \(\frac { \overline{b}+\overline{c} }{ √2 }\) then the angle between \(\overline { a }\) and \(\overline { b }\) is
(a) \(\frac { π }{ 2 }\)
(b) \(\frac { 3π }{ 4 }\)
(c) \(\frac { π }{ 4 }\)
(d) π
Solution:
(b) \(\frac { 3π }{ 4 }\)
Hint:

Question 11.
If the volume of the parallelepiped with \(\overline { a }\) × \(\overline { b }\), \(\overline { b }\) × \(\overline { c }\), \(\overline { c }\) × \(\overline { a }\) as coterminous edges is 8 cubic units, then the volume of the parallelepiped with (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { b }\) × \(\overline { c }\)), (\(\overline { b }\) × \(\overline { c }\)) × (\(\overline { c }\) × \(\overline { a }\)) and (\(\overline { c }\) × \(\overline { a }\)) × (\(\overline { a }\) × \(\overline { b }\)) as coterminous edges is
(a) 8 cubic units
(b) 512 cubic units
(c) 64 cubic units
(d) 24 cubic units
Solution:
(c) 64 cubic units
Hint:
Given volume of the parallelepiped with

Question 12.
Consider the vectors \(\overline { a }\), \(\overline { b }\), \(\overline { c }\), \(\overline { d }\) such that (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { c }\) × \(\overline { d }\)) = \(\overline { 0 }\) Let P₁ and P₂ be the planes determined by the pairs of vectors \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\), \(\overline { d }\) respectively. Then the angle between P₁ and P₂ is
(a) 0°
(b) 45°
(c) 60°
(d) 90°
Solution:
(a) 0°
Hint:
A vector perpendicular to the plane P₁ of a, b is \(\overline { a }\) × \(\overline { b }\),
A vector perpendicular to the plane P₂ of c and d is \(\overline { c }\) × \(\overline { d }\)
∴ (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { c }\) × \(\overline { d }\)) = 0
⇒ (\(\overline { a }\) × \(\overline { b }\)) || \(\overline { c }\) × \(\overline { d }\)
⇒ The angle between the planes is \(\overline { 0 }\)

Question 13.
If \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) = (\(\overline { a }\) × \(\overline { b }\)) × \(\overline { c }\) where \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are any three vectors such that \(\overline { b }\).\(\overline { c }\) ≠ 0 and \(\overline { a }\).\(\overline { b }\) ≠ 0, then \(\overline { a }\) and \(\overline { c }\) are
(a) perpendicular
(b) parallel
(c) inclined at angle \(\frac { π }{ 3 }\)
(d) inclined at an angle \(\frac { π }{ 6 }\)
Solution:
(b) parallel
Hint:

Question 14.
If \(\overline { a }\) = 2\(\hat { i }\) + 3\(\hat { j }\) – \(\hat { k }\), \(\overline { b }\) = \(\hat { i }\) + 2\(\hat { j }\) – 5\(\hat { k }\), \(\overline { c }\) = 3\(\hat { i }\) + 5\(\hat { j }\) – \(\hat { k }\) then \(\overline { a }\) vector perpendicular to a and lies in the plane containing \(\overline { b }\) and \(\overline { c }\) is
(a) -17\(\hat { i }\) + 21\(\hat { j }\) – 97\(\hat { k }\)
(b) 17\(\hat { i }\) + 21\(\hat { j }\) – 123\(\hat { k }\)
(c) -17\(\hat { i }\) – 21\(\hat { j }\) + 97\(\hat { k }\)
(d) -17\(\hat { i }\) – 21\(\hat { j }\) – 97\(\hat { k }\)
Solution:
(d) -17\(\hat { i }\) – 21\(\hat { j }\) – 97\(\hat { k }\)
Hint:
A vector ⊥r to \(\overline { a }\) and lies in the plane containing \(\overline { b }\) and \(\overline { c }\)

Question 15.
The angle between the lines \(\frac { x-2 }{ 3 }\) = \(\frac { y+1 }{ -2 }\), z = 2 and \(\frac { x-1 }{ 1 }\) = \(\frac { 2y+3 }{ 3 }\) = \(\frac { z+5 }{ 2 }\) is
(a) \(\frac { π }{ 6 }\)
(b) \(\frac { π }{ 4 }\)
(c) \(\frac { π }{ 3 }\)
(d) \(\frac { π }{ 2 }\)
Solution:
(d) \(\frac { π }{ 2 }\)
Hint:

Question 16.
If the line \(\frac { x-2 }{ 3 }\) = \(\frac { y-1 }{ -5 }\) = \(\frac { z+2 }{ 2 }\) lies in the plane x + 3y – αz + ß = 0 then (α + ß) is
(a) (-5, 5)
(b) (-6, 7)
(c) (5, -5)
(d) (6, -7)
Solution:
(b) (-6, 7)
Hint:
\(\frac { x-2 }{ 3 }\) = \(\frac { y-1 }{ 5 }\) = \(\frac { z+2 }{ 2 }\) = λ ⇒ (3λ + 2, -5λ + 1, 2λ – 2)
which lie in x + 3y – αz + ß = 0
(3λ + 2) + 3(-5λ + 1) – α(2λ – 2) + ß = 0
3λ + 2 – 15λ + 3 – 2αλ + 2α + ß = 0.
(-12λ – 2αλ) + 2α + ß + 5 = 0.
-12λ – 2αλ = 0
2αλ = -12λ
α = -6
2α+ ß +5 = 0
-12 + ß + 5 = 0
ß – 7 = 0
ß = 7
(α, ß) = (-6, 7)

Question 17.
The angle between the line \(\overline { r }\) = (\(\hat { i }\) + 2\(\hat { j }\) – 3\(\hat { k }\)) + t(2\(\hat { i }\) + \(\hat { j }\) – 2\(\hat { k }\)) and the plane \(\overline { r }\) (\(\hat { i }\) + \(\hat { j }\)) + 4 = 0 is
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Solution:
(c) 45°
Hint:

Question 18.
The co-ordinates of the point where the line \(\overline { r }\) = (6(\(\hat { i }\) – \(\hat { j }\) – 3\(\hat { k }\)) + t(-\(\hat { i }\) + \(\hat { k }\) meets the plane \(\overline { r }\) ((\(\hat { i }\) + (\(\hat { j }\) – (\(\hat { k }\)) = 3 are
(a) (2, 1, 0)
(b) (7, -1, -7)
(c) (1, 2, -6)
(d) (5, -1, 1)
Solution:
(d) (5, -1, 1)
Hint:
Given \(\overline { r }\) = (6(\(\hat { i }\) – (\(\hat { j }\) – 3(\(\hat { k }\)) + t(-(\(\hat { i }\) + (\(\hat { k }\))
\(\frac { x-6 }{ -1 }\) = \(\frac { y+1 }{ 0 }\) = \(\frac { z+3 }{ 4 }\) = t ⇒ (-t + 6, -1, 4t – 3)
which meets x + y – z = 3
-t + 6 – 1 – 4t + 3 = 3
-5t + 5 = 0
5t = 5
t = 1
∴ Co-ordinate is (5, -1, 1)

Question 19.
Distance from the origin to the plane 3x – 6y + 2z + 7 = 0 is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:
(x₁, y₁, z₁) = (o, 0, o)
(a, b, c) = (3, -6, 2); d = 7.
d = \(\frac { ax_1+by_1+cz_1+d }{ \sqrt{a^2+b^2+c^2} }\) = \(\frac { 7 }{ \sqrt{9+36+4} }\) = \(\frac { 7 }{ 7 }\) = 1

Question 20.
The distance between the planes
x + 2y + 3z + 7 = 0 and 2x + 4y + 6z + 7 = 0 is
(a) \(\frac { √7 }{ 2√2 }\)
(b) \(\frac { 7 }{ 2 }\)
(c) \(\frac { √7 }{ 2 }\)
(d) \(\frac { 7 }{ 2√2 }\)
Solution:
(a) \(\frac { √7 }{ 2√2 }\)
Hint:
x + 2y + 3z+7 = 0
2x + 4y + 6z + 7 = 0
(÷ 2) x + 2y + 3z + \(\frac { 7 }{ 2 }\) = 0
(1) and (2) are parallel planes

Question 21.
If the direction cosines of a line are \(\frac { 1 }{ c }\), \(\frac { 1 }{ c }\), \(\frac { 1 }{ c }\)
(a) c = ±3
(b) c = ±√3
(c) c > 0
(d) 0 < c < 1
Solution:
(b) c = ±√3
Hint:
cos²α + cos²ß + cos²γ = 1
\(\frac { 1 }{ c^2 }\) + \(\frac { 1 }{ c^2 }\) + \(\frac { 1 }{ c^2 }\) = 1
\(\frac { 3 }{ c ^2}\) = 1
c² = 3
c = ±√3

Question 22.
The vector equation \(\overline { r }\) = (\(\hat { i }\) – 2\(\hat { j }\) – \(\hat { k }\)) + t(6\(\hat { i }\) – \(\hat { k }\)) represents a straight line passing through the points
(a) (0, 6, -1) and (1, -2, -1)
(b) (0, 6, -1) and (-1, -4, -2)
(c) (1, -2, -1) and (1, 4, -2)
(d) (1, -2, -1) and (0, -6, 1)
Solution:
(c) (1, -2, -1) and (1, 4, -2)
Hint:
Given vector equation is

Question 23.
If the distance of the point (1, 1, 1) from the origin is half of its distance from the plane x + y + z + k = Q, then the values of k are
(a) ±3
(b) ±6
(c) -3, 9
(d) 3, -9
Solution:
(d) 3, -9
Hint:

Question 24.
If the planes \(\overline { r }\) (2\(\hat { i }\) – λ\(\hat { j }\) + \(\hat { k }\)) = 3 and \(\overline { r }\) (4\(\hat { i }\) + \(\hat { j }\) – µ\(\hat { k }\)) = 5 are parallel, then the value of λ and µ are
(a) \(\frac { 1 }{ 2 }\), -2
(b) –\(\frac { 1 }{ 2 }\), 2
(c) –\(\frac { 1 }{ 2 }\), -2
(d) \(\frac { 1 }{ 2 }\), 2
Solution:
(c) –\(\frac { 1 }{ 2 }\), -2
Hint:

Question 25.
If the length of the perpendicular from the origin to the plane 2x + 3y + λz = 1, λ > 0 is \(\frac { 1 }{ 5 }\), then the value of λ is
(a) 2√3
(b) 3√2
(c) 0
(d) 1
Solution:
(a) 2√3
Hint:

5 = \(\sqrt { 4+9+λ^2 }\)
25 = 4 + 9 + λ²
25 = 13 + λ²
λ² = 12
λ = 2√3

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.9 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.9

Question 1.
Find the equation of the plane passing through the line of intersection of the planes \(\overline { r }\) = (2\(\hat { i }\) – 7\(\hat { j }\) + 4\(\hat { k }\)) = 3 and 3x – 5y + 4z + 11 = 0 and the point (- 2, 1, 3).
Solution:
Given planes are
\(\vec{r} \cdot(2 \hat{i}-7 \hat{j}+4 \hat{k})\) = 3
2x – 7y + 4z – 3 = 0 and 3x – 5y + 4z + 11 = 0
Equation of a plane which passes through the line of intersection of the planes
(2x – 7y + 4z – 3) + λ(3x – 5y + 4z + 11) = 0 …………… (1)
This passes through the point (-2, 1, 3).
(1) ⇒ (-4 – 7 + 12 – 3) + λ(-6 – 5 + 12 + 11) = 0
-2 + λ(12) = 0 ⇒ 12λ = 2
λ = \(\frac{2}{12}\) ⇒ λ = \(\frac{1}{6}\)
The required equation is
(1) ⇒ (2x – 7y + 4z – 3) + \(\frac{1}{6}\) (3x – 5y + 4z + 11) = 0
12x – 42y + 24z – 18 + 3x – 5y + 4z + 11 = 0
15x – 47y + 28z – 7 = 0

Question 2.
Find the equation of the plane passing through the line of intersection of the planes x + 2y + 3z = 2 and x – y + z = 3 and at a distance \(\frac { 2 }{ √3 }\) from the point (3, 1, -1).
Solution:
Required equation of the plane
(x + 2y + 3z – 2) + λ(x – y + z – 3) = 0 ………. (1)
(1 + λ)x + (2 – λ)y + (3 + λ)z + (-2 – 3λ) = 0 ………(2)
Distance from (2) to the point (3, 1, -1) is \(\frac { 2 }{ √3 }\)

putting
λ = \(\frac { -7 }{ 2 }\) in (1)
The required equation
(x + 2y + 3z – 2) – \(\frac { 7 }{ 2 }\) (x – y + z – 3) = 0
2x + 4y + 6z – 4 – 7x + 7y – 7z + 21 = 0
-5x + 11y – z + 17 = 0
5x – 11y + z – 17 = 0

Question 3.
Find the angle between the line
\(\overline { r }\) = (2\(\hat { i }\) – \(\hat { j }\) + \(\hat { k }\)) + (\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\)) and the plane \(\overline { r }\) (6\(\hat { i }\) + 3\(\hat { j }\) + 2\(\hat { k }\)) = 8
Solution:

Question 4.
Find the angle between the planes \(\overline { r }\) (\(\hat { i }\) + \(\hat { j }\) – 2\(\hat { k }\)) = 3 and 2x – 2y + z = 2.
Solution:

Question 5.
Find the equation of the plane which passes through the point (3, 4, -1) and is parallel to the plane 2x – 3y + 5z + 7 = 0. Also, find the distance between the two planes.
Solution:
The required equation parallel to the plane
2x – 3y + 5z + 7 = 0 ………….. (1)
2x – 3y + 5z + λ = 0 ………….. (2)
This passes through (3, 4, -1)
(2) ⇒ 2(3) – 3(4) + 5(-1) + λ = 0
6 – 12 – 5 + 1 = 0
λ = 11
(2) ⇒ The required equation is 2x – 3y + 5z + 11 =0 …………… (3)
∴ Now, distance between the above parallel lines (1) and (3)
a = 2, b = -3, c = 5, d₁ = 7, d₂ = 11

Question 6.
Find the length of the perpendicular from the point (1, -2, 3) to the plane x – y + z = 5.
Solution:

Question 7.
Find the point of intersection of the line with the plane (x – 1) = \(\frac { y }{ 2 }\) = z + 1 with the plane 2x – y – 2z = 2. Also, the angle between the line and the plane.
Solution:
Any point on the line x – 1 = \(\frac{y}{2}\) = z + 1 is
x – 1 = \(\frac{y}{2}\) = z + 1 = λ,(say)
(λ + 1, 2λ, λ – 1)
This passes through the plane 2x – y + 2z = 2
2(λ + 1) – 2λ + 2(λ – 1) = 2
2λ + 2 – 2λ + 2λ – 2 = 2
λ = 1
∴ The required point of intersection is (2, 2, 0)

Question 8.
Find the co-ordinates of the foot of the perpendicular and length of the perpendicular from the point (4, 3, 2) to the plane x + 2y + 3z = 2.
Solution:
Let us take the point P(4, 3, 2) and Q(x₁, y₁, z₁)
⇒ (x₁ – 4, y₁ – 3, z₁ – 2)
Plane x + 2y + 3z = 2 ………. (1)
Cartesian equation of PQ, \(\frac { x_1-4 }{ 1 }\) = \(\frac { y_1-3 }{ 2 }\) = \(\frac { z_3-2 }{ 3 }\) = λ
(λ + 4, 2λ + 3, 3λ + 2) lies in (1)
(λ + 4) + 2(2λ + 3) + 3(3λ + 2) – 2 = 0
λ + 4 + 4λ + 6 + 9λ + 6 – 2 = 0
14λ + 14 = 0
14λ = -14 .
λ = -1
Co-ordinates of the foot of the ⊥r is (3, 1, -1).
Distance PQ = \(\sqrt{(4-3)^2 + (3-1)^2 + (2+1)^2}\)
= \(\sqrt{1^2 + 2^2 + 3^2}\) = \(\sqrt{1 + 4 + 9}\)
= \(\sqrt{14}\) units.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.8 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.8

Question 1.
Show that the straight lines
\(\overline { r }\) = (5\(\hat { i }\) + 7\(\hat { j }\) – 3\(\hat { k }\)) + s(4\(\hat { i }\) + 4\(\hat { j }\) – 5\(\hat { k }\)) and
\(\overline { r }\) = (8\(\hat { i }\) + 4\(\hat { j }\) + 5\(\hat { k }\)) + t(7\(\hat { i }\) + \(\hat { j }\) + 3\(\hat { k }\)) are coplanar. Find the vector equation of the, plane in which they lie.
Solution:

Question 2.
Show that the lines \(\frac { x-2 }{ 1 }\) = \(\frac { y-3 }{ 1 }\) = \(\frac { z -4}{ 3 }\) and \(\frac { x-1 }{ -3 }\) = \(\frac { y-4 }{ 2 }\) = \(\frac { z-5 }{ 1 }\) are coplanar. Also, find the plane containing these lines.
Solution:

Cartesian equation
x + 2y – 2z = 4
x + 2y – 2z – 4 = 0

Question 3.
If the straight lines \(\frac { x-1 }{ 1 }\) = \(\frac { y-2 }{ 2 }\) = \(\frac { z-3}{ m^2 }\) and \(\frac { x-3 }{ 1 }\) = \(\frac { y-2 }{ m^2 }\) = \(\frac { z-1 }{ 2 }\) are coplanar, find the distinct real values of m
Solution:

2(4 – m⁴) – 2(m² – 2) = 0
8 – 2m⁴ – 2m² + 4 = 0
12 – 2m⁴ – 2m² = 0
(÷ -2) -6 + m⁴ + m² = 0
m⁴ + m² – 6 = 0
(m² – 2)(m² + 3) = 0
m² – 2 = 2; m² = -3 (not possible)
m² = 2
m = ±√2

Question 4.
If the straight lines \(\frac { x-1 }{ 2 }\) = \(\frac { y+1 }{ λ }\) = \(\frac { z }{ 2 }\) and \(\frac { x+1 }{ 5 }\) = \(\frac { y+1 }{ 2 }\) = \(\frac { z }{ λ }\) are coplanar, find λ and equations of the planes containing these two lines.
Solution:
If the two lines are coplanar

When λ = 2
(x₁, y₁, z₁) = (1, -1, 0)
(b₁, b₂, b₃) = (2, 2, 2)
(d₁, d₂, d₃) = (5, 2, 2)
\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
b_{1} & b_{2} & b_{3} \\
d_{1} & d_{2} & d_{3}
\end{array}\right|\) = 0
⇒ \(\left|\begin{array}{ccc}
x-1 & y+1 & z-0 \\
2 & 2 & 2 \\
5 & 2 & 2
\end{array}\right|\) = 0
⇒ (x – 1)(0) – (y + 1)(-6) + z(6) = 0
⇒6(y + 1) – 6z = 0
⇒ 6y + 6 – 6z = 0
⇒ y – z + 1 = 0
When λ = 2
(b₁, b₂, b₃) = (2, -2, 2)
(d₁, d₂, d₃) = (5, 2, -2)
⇒ \(\left|\begin{array}{ccc}
x-1 & y+1 & z-0 \\
2 & -2 & 2 \\
5 & 2 & -2
\end{array}\right|\) = 0
⇒ (x – 1)(0) – (y + 1)(-14) + z(4 + 10) = 0
⇒ 14(y + 1) + 14z = 0
⇒ 14y + 14 + 14z = 0
⇒ y + z + 1 = 0

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.7 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.7

Question 1.
Find the non-parametric form of vector equation and Cartesian equation of the plane passing through the point (2, 3, 6) and parallel to the .straight lines.
\(\frac { x-1 }{ 2 }\) = \(\frac { y+1 }{ 3 }\) = \(\frac { z-3 }{ 1 }\) and \(\frac { x+3 }{ 2 }\) = \(\frac { y-3 }{ -5 }\) = \(\frac { z+1 }{ -3 }\)
Solution:

Question 2.
Find the non-parametric form of vector equation and Cartesian equations of the plane passing through the points (2, 2, 1), (9, 3, 6) and perpendicular to the plane 2x + 6y + 6z = 9.
Solution:

Cartesian equation
3x + 4y – 5z = 9
3x + 4y – 5z – 9 = 0

Question 3.
Find parametric form of vector equation and Cartesian equations of the plane passing through the points (2, 2, 1), (1, -2, 3) and parallel to the straight line passing through the points (2, 1, -3) and (-1, 5, -8)
Solution:

Cartesian equation
-12x + 11y + 16z = 14
12x – 11y – 16z = -14
12x – 11y – 16z + 14 = 0

Question 4.
Find the non-parametric form of vector equation and Cartesian equation of the plane passing through the point (1, -2, 4) and perpendicular to the plane x + 2y – 3z = 11 and parallel to the line \(\frac { x+7 }{ 3 }\) = \(\frac { y+3 }{ -1 }\) = \(\frac { z }{ 1 }\)
Solution:

Non parametric form

Which is the required Cartesian equation of the place.

Question 5.
Find the parametric form of vector equation and Cartesian equations of the plane containing
the line \(\overline { r }\) = (\(\hat { i }\) – \(\hat { j }\) + 3\(\hat { k }\)) + t(2\(\hat { i }\) – \(\hat { j }\) + 4\(\hat { k }\) ) and perpendicular to plane \(\overline { r }\) (\(\hat { i }\) + 2\(\hat { j }\) + \(\hat { k }\)) = 8
Solution:

Cartesian equation
9x – 2y – 5z = -4
9x – 2y – 5z + 4 = 0

Question 6.
Find the parametric vector non-parametric vector and Cartesian form of the equations of the plane passing through the three non- collinear points (3, 6, -2), (-1, -2, 6) and (6, 4, -2).
Solution:


Cartesian equation
⇒ \(\overline { r }\)(2\(\hat { i }\) + 3\(\hat { j }\) + 4\(\hat { k }\)) = 16
⇒ 2x + 3y + 4z – 16 = 0

Question 7.
Find the non-parametric form of vector equation and Cartesian equations of the plane
\(\overline { r }\) = (6\(\hat { i }\) – \(\hat { j }\) + \(\hat { k }\)) + s(\(\hat { -i }\) + 2\(\hat { j }\) + \(\hat { k }\)) + t(\(\hat { -5i }\) – 4\(\hat { j }\) – 5\(\hat { k }\))
Solution:

Cartesian equation:
3x + Sy – 7z = 6
3x + 5y – 7z – 6 = 0

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.6

Question 1.
Find a parametric form of vector equation of a plane which is at a distance of 7 units from t the origin having 3, -4, 5 as direction ratios of a normal to it.
Solution:
Let \(\overline { d }\) = \(\hat { i }\) – 4\(\hat { j }\) + 5\(\hat { k }\)
p = 7

Question 2.
Find the direction cosines of the normal to the plane 12x + 3y – 4z = 65. Also find the non-parametric form of vector equation of a plane and the length of the perpendicular to the plane from the origin.
Solution:

Length of the ⊥r from the origin = 5 units.

Question 3.
Find the vector and Cartesian equations of the plane passing through the point with position vector 2\(\hat { i }\) + 6\(\hat { j }\) + 3\(\hat { k }\) and normal to the vector \(\hat { i }\) + 3\(\hat { j }\) + 5\(\hat { k }\).
Solution:

Question 4.
A plane passes through the point (-1, 1, 2) and the normal to the plane of magnitude 3√3 makes equal acute angles with the co-ordinate axis. Find the equation of the plane.
Solution:
Magnitude = 3√2
Makes equal acute angles with co-ordinate axes l² + m² + n² = 1
cos²A + cos²A + cos²A = 1 ⇒ 3cos²A = 1
⇒ cos²A = \(\frac { 1 }{ 3 }\)
cos A = \(\frac { 1 }{ √3 }\)
\(\overline { n }\) (normal) = ±3√3(\(\frac { \hat{i} }{ √3 }\)+\(\frac { \hat{j} }{ √3 }\)+\(\frac { \hat{k} }{ √3 }\))
= ±(3\(\hat { i }\) + 3\(\hat { j }\) + 3\(\hat { k }\))
Equation of plane passing through (-1, 1, 2) normal (3, 3, 3)
⇒ 3(x + 1) + 3(y – 1) + 3(z – 2) = 0
⇒ 3x + 3 + 3y – 3 + 3z – 6 = 0
⇒ 3x + 3y + 3z – 6 = 0
⇒ x + y + z = 2
Vector equation \(\overline { r }\) (\(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\)) = 2

Question 5.
Find the intercepts cut off by the plane f \(\overline { r }\) (6\(\hat { i }\) + 4\(\hat { j }\) – 3\(\hat { k }\) ) = 12 on the co-ordinate axes
Solution:

x-intercept = 2, y-intercept = 3, z-intercept = -4

Question 6.
If a plane meets the co-ordinate axes at A, B, C such that the centroid of the triangle ABC is the point (u, v, w), find the equation of the plane.
Solution:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.5

Question 1.
Find the parametric form of vector equation and Cartesian equations of straight line passing through (5, 2, 8) and is perpendicular to the straight lines
\(\overline { r }\) = (\(\hat { i }\) + \(\hat { j }\) – \(\hat { k }\)) + s(2\(\hat { i }\) – 2\(\hat { j }\) + \(\hat { k }\)) and
\(\overline { r }\) = (2\(\hat { i }\) – \(\hat { j }\) – 3\(\hat { k }\)) + t(\(\hat { i }\) + 2\(\hat { j }\) + 2\(\hat { k }\)).
Solution:
Given points (5, 2, 8)

2\(\hat { i }\) + \(\hat { j }\) + 3\(\hat { k }\) is a vector perpendicular to both the given straight lines it passes through (5, 2, 8)
The equation is \(\overline { r }\) = (5\(\hat { i }\) + 2\(\hat { j }\) + 8\(\hat { k }\)) + t(2\(\hat { i }\) + \(\hat { j }\) – 2\(\hat { k }\))
Cartesian form = \(\frac { x-5 }{ 2 }\) = \(\frac { y-2 }{ 1 }\) = \(\frac { z-8 }{ -2 }\)

Question 2.
Show that the lines
\(\overline { r }\) = (6\(\hat { i }\) + \(\hat { j }\) + 2\(\hat { k }\)) + s(\(\hat { i }\) + 2\(\hat { j }\) – 3\(\hat { k }\)) and
\(\overline { r }\) = (3\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\)) + t(2\(\hat { i }\) + 4\(\hat { j }\) – 5\(\hat { k }\)) are skew lines and hence find the shortest distance between them.
Solution:

\(\overline { b }\) is not a scalar multiple of \(\overline { d }\)
∴ They are not parallel.
∴ The given lines are skew lines.

Question 3.
If the two lines \(\frac { x-1 }{ 2 }\) = \(\frac { y+1 }{ 3 }\) = \(\frac { z-1 }{ 4 }\) and \(\frac { x-3 }{ 1 }\) = \(\frac { y-m }{ 2 }\) = z intersect at a point, find the value of m.
Solution:
(x₁, y₁, z₁) = (1, -1, 1), (x₂, y₂, z₂) = (3, m, 0)
(₁, ₂, b₃) = (2, 3, 4), (d₁, d₂, d₃) = (1, 2, 1).

2(3 – 8) – (m + 1) (2 – 4) – 1(4 – 3) = 0
-10 – (m + 1) (-2) – 1(1) = 0
-10 + 2m + 2 – 1 = 0
2m – 9 = 0
2m = 9
m = \(\frac { 9 }{ 2 }\)

Question 4.
Show that the lines \(\frac { x-3 }{ 3 }\) = \(\frac { y-3 }{ -1 }\), z – 1 = 0 and \(\frac { x-6 }{ 2 }\) = \(\frac { z-1 }{ 3 }\), y – 2 = 0 intersect. Also find the point of intersection.
Solution:

(2s + 6, 2, 3s + 1) ……… (2)
(1) = (2)
((3t + 3), -t + 3, 1) = (2s + 6, 2, 3s + 1)
Compare on both sides
-t + 3 = 2; 3s + 1 = 1
t = 3 – 2; 3s = 0
t = 1; s = 0
(1) ⇒ Point of intersect (6, 2, 1)

Question 5.
Show that the straight lines x + 1 = 2y = -12z and x = y + 2 = 6z – 6 are skew and hence find the shortest distance between them.
Solution:
Given x + 1 = 2y = -12z

\(\overline { b }\) is not a scalar multiple of \(\overline { d }\). So, the two vectors are not parallel.
∴ The given lines are skew lines.

Question 6.
Find the parametric form of vector equation of the straight line passing through (-1, 2, 1) and parallel to the straight line
\(\overline { r }\) = (2\(\hat { i }\) + 3\(\hat { j }\) – \(\hat { k }\)) + t(\(\hat { i }\) – 2\(\hat { j }\) + \(\hat { k }\)) and hence find the shortest distance between the lines.
Solution:

Question 7.
Find the foot of the perpendicular drawn: from the point (5, 4, 2) to the line \(\frac { x+1 }{ 2 }\) = \(\frac { y-3 }{ 3 }\) = \(\frac { z-1 }{ -1 }\). Also, find the equation of the perpendicular.

Solution:
\(\overline { r }\) = \(\overline { a }\) + t\(\overline { b }\)
\(\overline { a }\) = -i + 3j + k, \(\overline { b }\) = 2i + 3j – k
Given points D (5, 4, 2) to the point A. If P is the foot of the perpendicular from to the straight line.
F is of the form
(2t – 1, 3t + 3, -t + 1) and
\(\overline { DF }\) = \(\overline { OF }\) – \(\overline { OD }\) = (2t – 6)i + (3t – 1)j + (-t – l)k
\(\overline { b }\) is perpendicular to \(\overline { DF }\), we have
\(\overline { b }\).\(\overline { DF }\) = 0 => (2t – 6) 2 + 3(3t – 1) – 1(-t – 1) = 0
4t- 12 + 9t – 3 + t + 1 = 0
14t – 14 = 0
14t = 14
t = 1
∴ F (2 – 1, 3 + 3, -1 + 1) = F (1, 6, 0) is foot point. Equation of the perpendicular.
(x₁, y₁, z₁) = (5, 4, 2), (x₂, y₂, z₂) = (1, 6, 0).

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.4

Question 1.
Find the non-parametric form of vector equation and Cartesian equations of the straight line passing through the point with position vector 4\(\hat { i }\) + 3\(\hat { j }\) – 7\(\hat { k }\) and parallel to the vector 2\(\hat { i }\) – 6\(\hat { j }\) + 7\(\hat { k }\)
Solution:

Question 2.
Find the parametric form of vector equation and Cartesian equations of the straight line passing through the point (-2, 3, 4) and parallel to the straight line \(\frac { x-1 }{ -4 }\) = \(\frac { y+3 }{ 5 }\) = \(\frac { 8-z }{ 6 }\)
Solution:
\(\overline { a }\) = -2\(\hat { i }\) + 3\(\hat { j }\) + 4\(\hat { k }\) (x₁, y₁, z₁) = (-2, 3, 4)
\(\overline { b }\) = -4\(\hat { i }\) + 5\(\hat { j }\) + 6\(\hat { k }\) (l, m, n) = (-4, 5, 6)
vector equation

Question 3.
Find the points where the straight line passes through (6, 7, 4) and (8, 4, 9) cuts the xz and yz planes.
Solution:
The straight line passes through the points (6, 7, 4) and (8, 4, 9)
∴ Direction ratios are 2, -3, 5
So the straight line is parallel to 2\(\hat { i }\) – 3\(\hat { j }\) + 5\(\hat { k }\)
∴ Vector equation is

An arbitrary point on the straight line is of the form (2t + 6, -3t + 7, 5t + 4) or (2s + 8, -3s + 4, 5s + 9)
(i) xz plane mean y = 0
-3t + 7 = 0
3t = 7
t = \(\frac { 7 }{ 3 }\)
Point = (2(\(\frac { 7 }{ 3 }\)) + 6, 0, 5(\(\frac { 7 }{ 3 }\)) + 4) = (\(\frac { 32 }{ 3 }\), 0, \(\frac { 47 }{ 3 }\))

(ii) The straight Line cuts yz-plane
So we get x = 0
2t + 6 = 0 ⇒ 2t = -6
t = -3
-3t + 7 = -3 (-3) + 7 = 9 + 7 = 16
5t + 4 = 5(-3) + 4 = -15 + 4 = -11
The required point (0, 16, -11).

Question 4.
Find the direction cosines of the straight line passing through the points (5, 6, 7) and (7, 9, 13). Also, find the parametric form of vector equation and Cartesian equations of the straight line passing through two given points.
Solution:
Given points (5, 6, 7) and (7, 9, 13)
Direction ratios are (2, 3, 6)
So the straight line is parallel to 2\(\hat { i }\) + 3\(\hat { j }\) + 6\(\hat { k }\)

Question 5.
Find the acute angle between the following lines. ]
(i) \(\overline { r }\) = (4\(\hat { i }\) – \(\hat { j }\)) + t(\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\)),
\(\overline { r }\) = (\(\hat { i }\) – 2\(\hat { j }\) + 4\(\hat { k }\)) + s(-\(\hat { i }\) – 2\(\hat { j }\) + 2\(\hat { k }\))
(ii) \(\frac { x+4 }{ 3 }\) = \(\frac { y-7 }{ 4 }\) = \(\frac { z+5 }{ 5 }\), \(\overline { r }\) = 4\(\hat { k }\) + t(2\(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\))
(iii) 2x = 3y = -z and 6x = -y = -4z.
Solution:

Question 6.
The vertices of ΔABC are A(7, 2, 1), 5(6, 0, 3), and C(4, 2, 4). Find ∠ABC.
Solution:

Question 7.
If the straight line joining the points (2, 1, 4) and (a – 1, 4, -1) is parallel to the line joining the points (0, 2, b – 1) and (5, 3, -2) find the values of a and b.
Solution:
(i) Points are (2, 1, 4) (a – 1, 4, -1)
Cartesian equation

(ii) Points are (0, 2, b – 1) (5, 3, -2)
Cartesian equation

Question 8.
If the straight lines \(\frac { x-5 }{ 5m+2 }\) = \(\frac { 2-y }{ 5 }\) = \(\frac { 1-z }{ -1 }\) and x = \(\frac { 2y+1 }{ 4ni }\) = \(\frac { 1-z }{ -3 }\) are perpendicular to each other, find the value of m.
Solution:
If the lines are perpendicular
b₁d₁ + b₂d₂ + b₃d₃ = 0
(5m + 2) – 5(2m) + 1(+3) = 0
5m + 2 – 10m + 3 = 0
-5m = -5
m = \(\frac { -5 }{ -5 }\) = 1
⇒ ∴ m = 1

Question 9.
Show that the points (2, 3, 4), (-1, 4, 5) and (8, 1, 2) are collinear.
Solution:

∴ given points are collinear.