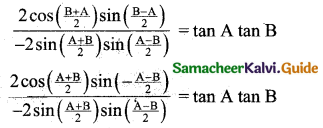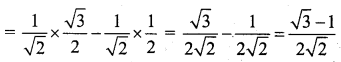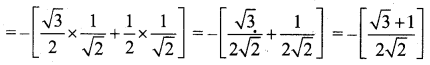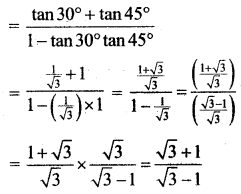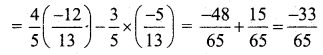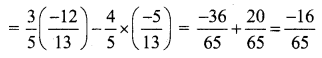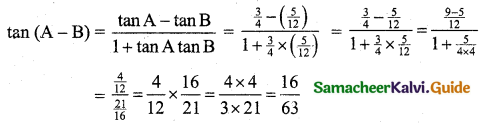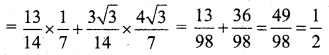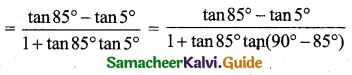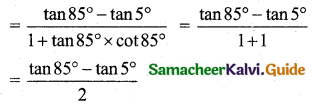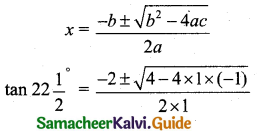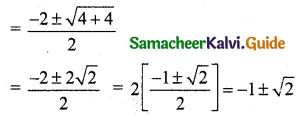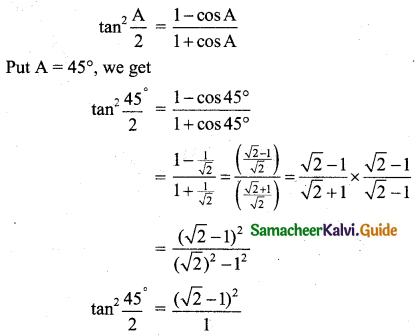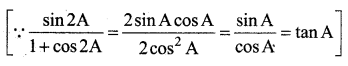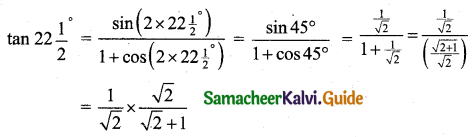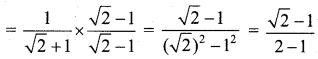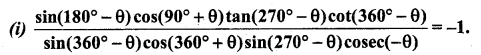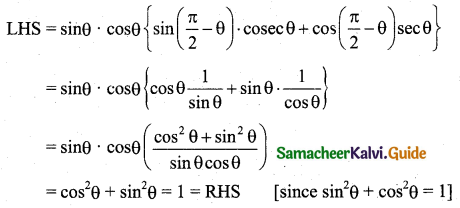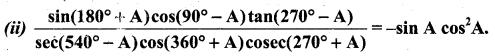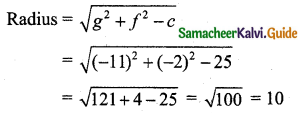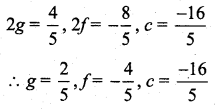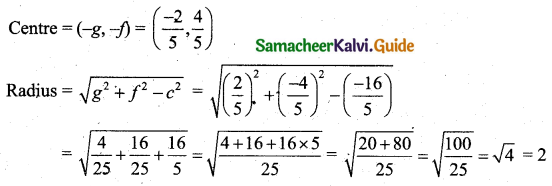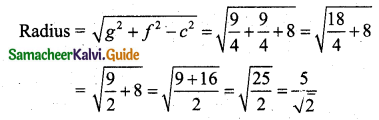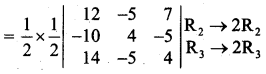Category: Class 11

Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.3

Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.3 Text Book Back Questions and Answers

Question 1.
Express each of the following as the sum or difference of sine or cosine:
(i) sin\(\frac{A}{8}\) sin\(\frac{3A}{8}\)
(ii) cos(60° + A) sin(120° + A)
(iii) cos\(\frac{7 A}{3}\) sin\(\frac{5 A}{3}\)
(iv) cos 7θ sin 3θ
Solution:
(i) sin\(\frac{A}{8}\) sin\(\frac{3A}{8}\)

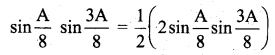
[∵ 2 sin A sin B = cos(A – B) – cos(A + B)

[∵ cos(-θ) = cos θ]

(ii) cos(60° + A) sin(120° + A) = \(\frac{1}{2}\) [2 cos(60° + A) sin(120° + A)] [Multiply and divide by 2]
= \(\frac{1}{2}\) [sin((60° + A) + (120° + A))] – sin((60° + A) – (120° + A))]
[∵ 2 cos A sin B = sin(A + B) – sin(A – B)]
= \(\frac{1}{2}\) [sin(180° + 2A) – sin(60° + A – 120° – A)]
= \(\frac{1}{2}\) [(-sin 2A) – sin(-60°)]
= \(\frac{1}{2}\) [-sin 2A + sin 60°]
= \(\frac{1}{2}\) [-sin 2A + \(\frac{\sqrt{3}}{2}\)]

(iii) cos\(\frac{7 A}{3}\) sin\(\frac{5 A}{3}\)

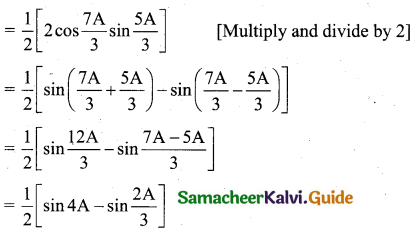
(iv) cos 7θ sin 3θ = \(\frac{1}{2}\) [sin(7θ + 3θ) – sin(7θ – 3θ)]
= \(\frac{1}{2}\) (sin 10θ – sin 4θ)

Question 2.
Express each of the following as the product of sine and cosine
(i) sin A + sin 2A
(ii) cos 2A + cos 4A
(iii) sin 6θ – sin 2θ
(iv) cos 2θ – cos θ
Solution:
(i) sin A + sin 2A = 2 sin(\(\frac{A+2 A}{2}\)) cos(\(\frac{A-2 A}{2}\))
[∵ sin C + sin D = sin(\(\frac{C+D}{2}\)) cos(\(\frac{C-D}{2}\))]
= 2 sin \(\frac{3A}{2}\) cos \(\frac{A}{2}\) [∵ cos(-θ) = cos θ]

(ii) cos 2A + cos 4A = 2 cos(\(\frac{2 \mathrm{A}+4 \mathrm{A}}{2}\)) cos(\(\frac{2 \mathrm{A}-4 \mathrm{A}}{2}\))
[∵ cos C + cos D = 2 cos(\(\frac{C+D}{2}\)) cos(\(\frac{C-D}{2}\))
= 2 cos(\(\frac{6 \mathrm{A}}{2}\)) cos(\(\frac{6 \mathrm{-2A}}{2}\))
= 2 cos(3A) cos (-A) [∵ cos(-θ) = cos θ]
= 2 cos 3A cos A

(iii) sin 6θ – sin 2θ = 2 cos(\(\frac{6 \theta+2 \theta}{2}\)) cos(\(\frac{6 \theta-2 \theta}{2}\))
[∵ sin C – sin D = 2 cos(\(\frac{C+D}{2}\)) sin(\(\frac{C-D}{2}\))
= 2 cos(\(\frac{8 \theta}{2}\)) sin(\(\frac{4 \theta}{2}\))
= 2 cos 4θ sin 2θ

(iv) cos 2θ – cos θ = -2 sin(\(\frac{2 \theta+\theta}{2}\)) sin(\(\frac{2 \theta-\theta}{2}\))
[∵ cos C – cos D = -2 sin(\(\frac{C+D}{2}\)) sin(\(\frac{C-D}{2}\))
= -2 sin(\(\frac{3 \theta}{2}\)) sin(\(\frac{\theta}{2}\))

Question 3.
Prove that
(i) cos 20° cos 40° cos 80° = \(\frac{1}{8}\)
(ii) tan 20° tan 40° tan 80° = √3.
Solution:
(i) cos 20° cos 40° cos 80° = \(\left(\frac{2 \sin 20^{\circ}}{2 \sin 20^{\circ}}\right)\) cos 20° cos 40° cos 80°
[multiply and divide by 2 sin 20°]

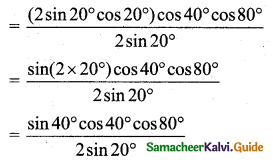
(Multiply and divide by 2)


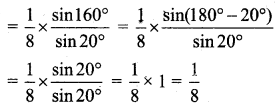
[∵ sin(180° – θ) = sin θ]

(ii) tan 20° tan 40° tan 80°

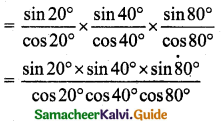
Consider sin 20° × sin 40° sin 80°
= sin 20° sin (60° – 20°) sin (60° + 20°)
= sin 20° [sin² 60° – sin² 20°]

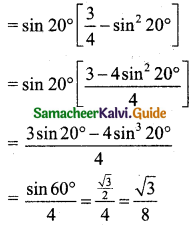
cos 20° × cos 40° cos 80° = \(\frac{1}{8}\) [∵ from (i)] …… (2)
divide (1) by (2) we get, tan 20° tan 40° tan 80° = \(\frac{\frac{\sqrt{3}}{8}}{\frac{1}{8}}\) = √3

Question 4.
Prove that
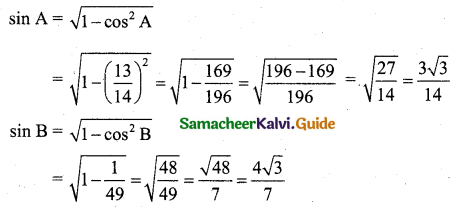
(i) (cos α – cos β)² + (sin α – sin β)² = 4 \(\sin ^{2}\left(\frac{\alpha-\beta}{2}\right)\)
(ii) sin A sin(60° + A) sin(60° – A) = sin 3A
Solution:
(i) LHS = (cos α – cos β)² + (sin α – sin β)²

(ii) LHS = 4 sin A sin (60° + A) . sin (60° – A)
= 4 sin A {sin (60° + A) . sin (60° – A)}
= 4 sin A {sin² 60° – sin² A}
= 4 sin A {\(\frac{3}{4}\) – sin² A}
= 3 sin A – 4 sin³ A
= sin 3A
= RHS

Question 5.
Prove that
(i) sin (A – B) sin C + sin (B – C) sin A + sin(C – A) sin B = 0
(ii) \(2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}=0\)
Solution:
Consider sin (A – B) sin C
= (sin A cos B – cos A sin B) sin C
= sin A cos B sin C – cos A sin B sin C …….. (1)
Similarly sin(B – C) sin A = sin B cos C sin A – cos B sin C sin A …….. (2)
[Replace A by B, B by C, C by A in (1)]
and sin(C – A) sin B [Replace A by B, B by C, C by A in (2)]
= sin C cos A sin B – cos C sin A sin B …….. (3)
Adding (1), (2) and (3) we get
sin (A – B) sin C + sin (B – C) sin A + sin(C – A) sin B = 0

(ii) \(2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}=0\)

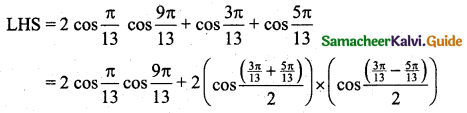
[∵ cos C + cos D = 2 cos(\(\frac{C+D}{2}\)) cos(\(\frac{C-D}{2}\))]

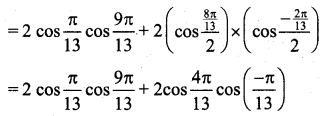
[∵ cos(-θ) = cos θ]

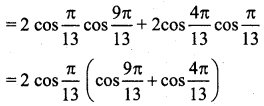
[take 2 cos \(\frac{\pi}{3}\) as commom)

Hence proved.

Question 6.
Prove that
(i) \(\frac{\cos 2 A-\cos 3 A}{\sin 2 A+\sin 3 A}=\tan \frac{A}{2}\)
(ii) \(\frac{\cos 7 \mathbf{A}+\cos 5 \mathbf{A}}{\sin 7 \mathbf{A}-\sin 5 \mathbf{A}}=\cot \mathbf{A}\)
Solution:
(i) \(\frac{\cos 2 A-\cos 3 A}{\sin 2 A+\sin 3 A}=\tan \frac{A}{2}\)

(ii) \(\frac{\cos 7 \mathbf{A}+\cos 5 \mathbf{A}}{\sin 7 \mathbf{A}-\sin 5 \mathbf{A}}=\cot \mathbf{A}\)



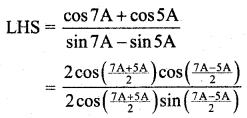
Hence proved.

Question 7.
Prove that cos 20° cos 40° cos 60° cos 80° = \(\frac{3}{16}\).
Solution:
LHS = cos 20° cos 40° cos 60° cos 80°
= cos 20° cos 40° (\(\frac{1}{2}\)) cos 80° [∵ cos 60° = \(\frac{1}{2}\)]
= \(\frac{1}{2}\) (cos 20° cos 40° cos 80°)
= \(\frac{1}{2}\left(\frac{2 \sin 20^{\circ}}{2 \sin 20^{\circ}}\right)\) (cos 20° cos 40° cos 80°)
[multiply and divide by 2 sin 20°]

[multiply and divide by 2]

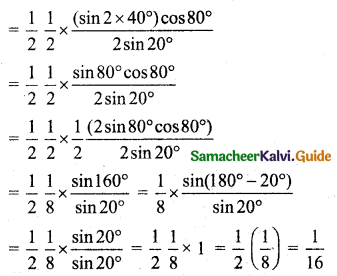
Hence Proved.

Question 8.
Evaluate:
(i) cos 20° + cos 100° + cos 140°
(ii) sin 50° – sin 70° + sin 10°
Solution:
(i) LHS = (cos 20° + cos 100°) + cos 140°
= 2 \(\cos \left(\frac{20^{\circ}+100^{\circ}}{2}\right) \cos \left(\frac{20^{\circ}-100^{\circ}}{2}\right)\) + cos 140°
[∵ cos C + cos D = 2 cos(\(\frac{C+D}{2}\)) cos(\(\frac{C-D}{2}\))]
= 2 cos 60° cos(-40°) + cos 140°
= 2 × \(\frac{1}{2}\) × cos(-40°) + cos(180° – 140°)
[∵ cos(-θ) = cos θ, cos 60° = \(\frac{1}{2}\)
= cos 40° – cos 40°
= 0
Hence Proved.

(ii) LHS = (sin 50° – sin 70°) + sin 10°
= 2 \(\cos \left(\frac{50^{\circ}+70^{\circ}}{2}\right) \sin \left(\frac{50^{\circ}-70^{\circ}}{2}\right)\) + sin 10°
[∵ sin C – sin D = 2 cos(\(\frac{C+D}{2}\)) sin(\(\frac{C-D}{2}\))]
= 2 cos 60° sin(-10°) + sin 10°
= 2 × \(\frac{1}{2}\) (-sin 10°) + sin 10° [∵ sin(-θ) = -sin θ]
= -sin 10° + sin 10°
= 0
= RHS

Question 9.
If cos A + cos B = \(\frac{1}{2}\) and sin A + sin B = \(\frac{1}{4}\), prove that \(\tan \left(\frac{\mathbf{A}+\mathbf{B}}{2}\right)=\frac{\mathbf{1}}{2}\)
Solution:
Given that cos A + cos B = \(\frac{1}{2}\)
\(2 \cos \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)=\frac{1}{2}\) …….. (1)
Also given that sin A + sin B = \(\frac{1}{4}\)
\(2 \sin \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)=\frac{1}{4}\) ……. (2)
\(\frac{(2)}{(1)}\) gives

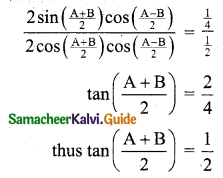
Question 10.
If sin(y + z – x), sin(z + x – y), sin(x + y – z) are in A.P, then prove that tan x, tan y and tan z are in A.P.
Solution:
In A.P. commom difference are equal, namely t₂ – t₁ = t₃ – t₂
sin(z + x – y) – sin(y + z – x) = sin(x + y – z) – sin(z + x – y)


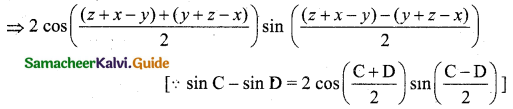
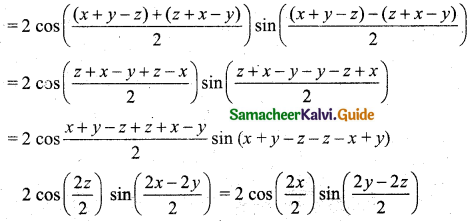
cos z sin (x – y) = cos x sin (y – z)
cos z (sin x cos y – cos x sin y) = cos x (sin y cos z – cos y sin z)
Divide bothsides by cos x cos y cos z we get

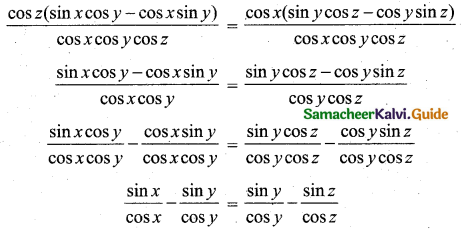
tan x – tan y = tan y – tan z
Multiply both sides by (-1) we get,
tan y – tan x = tan z – tan y
This means tan x, tan y, and tan z are in A.P.
Hence proved.

Question 11.
If cosec A + sec A = cosec B + sec B prove that cot(\(\frac{A+B}{2}\)) = tan A tan B.
Solution:
Given that cosec A + sec A = cosec B + sec B

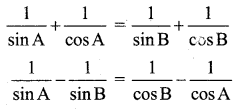
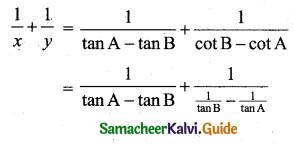
Arrange T-ratios of the sine and cosine in the separate side

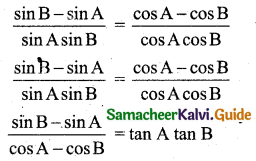
[∵ sin C – sin D = 2 cos(\(\frac{C+D}{2}\)) sin(\(\frac{C-D}{2}\))]

Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.2 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.2

Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.2 Text Book Back Questions and Answers

Question 1.
Find the values of the following:
(i) cosec 15°
(ii) sin (-105°)
(iii) cot 75°
Solution:
(i) cosec 15° = \(\frac{1}{\sin 15^{\circ}}\)
Consider sin 15° = sin(45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°

cosec 15° = \(\frac{1}{\sin 15^{\circ}}\) = \(\frac{2 \sqrt{2}}{\sqrt{3}-1}\)

(ii) sin (-105°) = -sin (105°) (∵ sin (-θ) = – sin θ)
= -[sin(60° + 45°)]
= -[sin 60° cos 45° + cos 60° sin 45°]

(iii) cot 75° = \(\frac{1}{\tan 75^{\circ}}\)
Consider tan 75° = tan (30° + 45°)

cot 75° = \(\frac{1}{\tan 75^{\circ}}=\frac{\sqrt{3}-1}{\sqrt{3}+1}\)

Question 2.
Find the values of the following:
(i) sin 76° cos 16° – cos 76° sin 16°
(ii) \(\sin \frac{\pi}{4} \cos \frac{\pi}{12}+\cos \frac{\pi}{4} \sin \frac{\pi}{12}\)
(iii) cos 70° cos 10° – sin 70° sin 10°
(iv) cos² 15° – sin² 15°
Solution:
(i) Given that, sin 76° cos 16° – cos 76° sin 16° (∴ This is of the form sin(A – B))
= sin(76° – 16°)
= sin 60°
= \(\frac{\sqrt{3}}{2}\)

(ii) This is of the form sin(A + B) = \(\sin \left(\frac{\pi}{4}+\frac{\pi}{12}\right)\)
= \(\sin \left(\frac{3 \pi+\pi}{12}\right)\)
= \(\sin \frac{4 \pi}{12}\)
= \(\sin \frac{\pi}{3}\)
= \(\frac{\sqrt{3}}{2}\) (∵ sin 60° = \(\frac{\sqrt{3}}{2}\))

(iii) Given that cos 70° cos 10° – sin 70° sin 10°
(This is of the form of cos (A + B), A = 70°, B = 10°)
= cos (70° + 10°)
= cos 80°

(iv) cos² 15° – sin² 15°
[∵ cos 2A = cos² A – sin² A, Here A = 15°]
= cos (2 × 15°)
= cos 30°
= \(\frac{\sqrt{3}}{2}\)

Question 3.
If sin A = \(\frac{3}{5}\), 0 < A < \(\frac{\pi}{2}\) and cos B = \(\frac{-12}{13}\), π < B < \(\frac{3 \pi}{2}\), find the values of the following:
(i) cos(A + B)
(ii) sin(A – B)
(iii) tan(A – B)
Solution:
Given that sin A = \(\frac{3}{5}\), 0 < A < \(\frac{\pi}{2}\) (i.e., A lies in first quadrant)
Since A lies in first quadrant cos A is positive.

cos A = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}=\frac{4}{5}\)
tan A = \(\frac{3}{4}\)
AB = \(\sqrt{5^{2}-3^{2}}\) = 4
Also given that cos B = \(\frac{-12}{13}\), π < B < \(\frac{3 \pi}{2}\) (i.e., B lies in third quadrant)
Now sin B lies in third quadrant. sin B is negative.

CA = \(\sqrt{13^{2}-12^{2}}\) = 5
sin B = \(\frac{-\text { Opposite side }}{\text { Hypotenuse }}=\frac{-5}{13}\)
tan B = \(\frac{-\text { Opposite side }}{\text { Adjacent }}=\frac{5}{12}\) [B lies in 3rd quadrant. tan B is positive.]
(i) cos(A + B) = cos A cos B – sin A sin B

(ii) sin(A – B) = sin A cos B – cos A sin B

(iii) tan(A – B)

Question 4.
If cos A = \(\frac{13}{14}\) and cos B = \(\frac{1}{7}\) where A, B are acute angles prove that A – B = \(\frac{\pi}{3}\)
Solution:
cos A = \(\frac{13}{14}\), cos B = \(\frac{1}{7}\)

cos(A – B) = cos A cos B + sin A sin B

cos(A – B) = cos 60°
A – B = 60° = \(\frac{\pi}{3}\)

Question 5.
Prove that 2 tan 80° = tan 85° – tan 5°.
Solution:
Consider tan 80° = tan(85° – 5°)


∴ 2 tan 80° = tan 85° – tan 5°
Hence Proved.

Question 6.
If cot α = \(\frac{1}{2}\), sec β = \(\frac{-5}{3}\), where π < α < \(\frac{3 \pi}{2}\) and \(\frac{\pi}{2}\) < β < π, find the value of tan(α + β). State the quadrant in which α + β terminates.
Solution:
Given that cot α = \(\frac{1}{2}\) where π < α < \(\frac{3 \pi}{2}\) (i.e,. α lies in third quadrant)
tan α = \(\frac{1}{\frac{1}{2}}\) = 2 [∵ In 3rd quadrant tan α is positive]
Also given that sec β = \(\frac{-5}{3}\) where \(\frac{\pi}{2}\) < β < π (i.e., β lies in second quadrant cos β and tan β are negative)


tan (α + β) = \(\frac{2}{11}\) which is positive.
α + β terminates in first quandrant.

Question 7.
If A + B = 45°, prove that (1 + tan A) (1 + tan B) = 2 and hence deduce the value of tan 22\(\frac{1}{2}\).
Solution:
Given A + B = 45°
tan (A + B) = tan 45°
\(\frac{\tan A+\tan B}{1-\tan A \tan B}=1\)
tan A + tan B = 1 – tan A . tan B
tan A + tan B + tan A tan B = 1
Add 1 on both sides we get,
(1 + tan A) + tan B + tan A tan B = 2
1(1+ tan A) + tan B (1 + tan A) = 2
(1 + tan A) (1 + tan B) = 2 ……. (1)
Put A = B = 22\(\frac{1}{2}\) in (1) we get
(1 + tan 22\(\frac{1}{2}\)) (1 + tan 22\(\frac{1}{2}\)) = 2
⇒ (1 + tan22\(\frac{1}{2}\))² = 2
⇒ 1 + tan 22\(\frac{1}{2}\) = ±√2
⇒ tan 22\(\frac{1}{2}\) = ±√2 – 1
Since 22\(\frac{1}{2}\) is acute, tan 22\(\frac{1}{2}\) is positive and therefore tan 22\(\frac{1}{2}\) = √2 – 1

Question 8.
Prove that
(i) sin(A + 60°) + sin(A – 60°) = sin A.
(ii) tan 4A tan 3A tan A + tan 3A + tan A – tan 4A = 0
Solution:
(i) LHS = sin (A + 60°) + sin (A – 60°)
= sin A cos 60° + cos A sin 60° + sin A cos 60° – cos A sin 60°
= 2 sin A cos 60°
= 2 sin A \(\left(\frac{1}{2}\right)\)
= sin A
= RHS

(ii) 4A = 3A + A
tan 4A = tan (3A + A)
tan 4A = \(\frac{\tan 3 \mathrm{A}+\tan \mathrm{A}}{1-\tan 3 \mathrm{A} \tan \mathrm{A}}\)
on cross multiplication we get,
tan 3A + tan A = tan 4A (1 – tan 3A tan A) = tan 4A – tan 4A tan 3A tanA
i.e., tan 4A tan 3A tan A + tan 3A + tan A = tan 4A
(or) tan 4A tan 3A tan A + tan 3A + tan A – tan 4A = 0

Question 9.
(i) If tan θ = 3 find tan 3θ
(ii) If sin A = \(\frac{12}{13}\), find sin 3A.
Solution:
(i) tan θ = 3

(ii) If sin A = \(\frac{12}{13}\)
We know that sin 3A = 3 sin A – 4 sin³ A

Question 10.
If sin A = \(\frac{3}{5}\), find the values of cos 3A and tan 3A.
Solution:

Given sin A = \(\frac{3}{5}\)
cos A = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}=\frac{4}{5}\)
and tan A = \(\frac{\text { Opposite side }}{\text { Adjacent side }}=\frac{3}{4}\)
We know that cos 3A = 4 cos³ A – 3 cos A

Question 11.
Prove that \(\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}+\frac{\sin (A-B)}{\cos A \cos B}=0\)
Solution:
Consider \(\frac{\sin (B-C)}{\cos B \cos C}\)
= \(\frac{\sin \mathrm{B} \cos \mathrm{C}-\cos \mathrm{B} \sin \mathrm{C}}{\cos \mathrm{B} \cos \mathrm{C}}\)
= \(\frac{\sin B \cos C}{\cos B \cos C}-\frac{\cos B \sin C}{\cos B \cos C}\)
= tan B – tan C ……… (1)
Similarly we can prove \(\frac{\sin (C-A)}{\cos C \cos A}\) = tan C – tan A …….(2)
and \(\frac{\sin (A-B)}{\cos A \cos B}\) = tan A – tan B …….. (3)
Add (1), (2) and (3) we get
\(\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}+\frac{\sin (A-B)}{\cos A \cos B}=0\)

Question 12.
If tan A – tan B = x and cot B – cot A = y prove that cot(A – B) = \(\frac{1}{x}+\frac{1}{y}\).
Solution:


Hence proved.

Question 13.
If sin α + sin β = a and cos α + cos β = b, then prove that cos(α – β) = \(\frac{a^{2}+b^{2}-2}{2}\)
Solution:
Consider a² + b² = sin²α + sin²β + 2 sin α sin β + cos²α + cos²β + 2 cos α cos β
a² + b² = (sin²α + cos²α) + (sin²β + cos²β) + 2[cos α cos β + sin α sin β]
a² + b² = 1 + 1 + 2 cos(α – β)
∴ cos(α – β) = \(\frac{a^{2}+b^{2}-2}{2}\)

Question 14.
Find the value of tan\(\frac{\pi}{8}\).
Solution:
Method 1:
\(\frac{\pi}{8}=\frac{180^{\circ}}{8}=\frac{45^{\circ}}{2}=22 \frac{1}{2}\)
We know that tan 2A = \(\frac{2 \tan A}{1-\tan ^{2} A}\)
Put A = 22\(\frac{1}{2}\) in the above formula

On cross multiplication we get


Here a = 1, b = 2, c = -1

Since 22\(\frac{1}{2}\) is acute tan 22\(\frac{1}{2}\) is positive tan 22\(\frac{1}{2}\) = tan \(\frac{\pi}{8}\)
= -1 + √2
= √2 – 1

Method 2:



∴ \(\tan ^{2} 22 \frac{1}{2}=(\sqrt{2}-1)^{2}\)
Taking square root, \(\tan ^{2} 22 \frac{1}{2}\) = ±(√2 – 1)
But \(22 \frac{1}{2}\) lies in first quadrant, tan \(22 \frac{1}{2}\) is positive.
∴ tan 22\(\frac{1}{2}\) = √2 – 1

Method 3:
consider tan A = \(\frac{\sin 2 A}{1+\cos 2 A}\)
Put A = \(22 \frac{1}{2}\)



tan 22\(\frac{1}{2}\) = √2 – 1

Question 15.
If tan α = \(\frac{1}{7}\), sin β = \(\frac{1}{\sqrt{10}}\). Prove that α + 2β = \(\frac{\pi}{4}\) where 0 < α < \(\frac{\pi}{2}\) and 0 < β < \(\frac{\pi}{2}\).
Solution:
Given that tan α = \(\frac{1}{7}\)
We wish to find tan(α + 2β)

Subject Matter Experts at SamacheerKalvi.Guide have created Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern 11th Model Question Papers 2020-2021 with Answers Pdf Free Download in English Medium and Tamil Medium of TN 11th Standard Public Exam Question Papers Answer Key, New Paper Pattern of HSC 11th Class Previous Year Question Papers, Plus One +1 Model Sample Papers, Tamil Nadu 11th Quarterly Half Yearly Model Question Papers are part of Samacheer Kalvi.

Let us look at these Tamil Nadu Government 11th State Board Model Question Papers with Answers for All Subjects 2020-21 Tamil Medium Pdf. Students can view or download the Class 11th New Model Question Papers 2021 Tamil Nadu English Medium Pdf for their upcoming Tamil Nadu HSC Board Exams. Students can also read Tamilnadu Samcheer Kalvi 11th Books Solutions.

The higher officials of Tamil Nadu Directorate of Government Examinations conducts Public examination to Class 11 Students in the month of March. Recently Government of Tamil Nadu has made changes in the examination pattern to reduce the pressure and tension in students. Here we have provided the Tamil Nadu 11th Model Question Papers PDF, students can view and download the latest pdf of 11th Model Question Papers. Before preparing for the public examinations students need to know about TN 11th Model Question Papers. These Model Papers helps students to prepare well. In this page, we have provided all subject wise Tamil Nadu Plus One Model Question Papers. Before appearing for HSC examinations students must practice all the TN Model Question Papers to score high marks in TN Plus One Examinations.

11th New Public Exam Model Question Papers Tamil Nadu 2020 2021 English Tamil Medium

11th New Model Question Papers 2020 2021 Tamil Nadu

• Tamil Nadu 11th Maths Model Question Papers
• Tamil Nadu 11th Physics Model Question Papers
• Tamil Nadu 11th Chemistry Model Question Papers
• Tamil Nadu 11th Biology Model Question Papers
• Tamil Nadu 11th English Model Question Papers
• Tamil Nadu 11th Tamil Model Question Papers
• Tamil Nadu 11th Commerce Model Question Papers
• Tamil Nadu 11th Economics Model Question Papers
• Tamil Nadu 11th Accountancy Model Question Papers
• Tamil Nadu 11th Computer Science Model Question Papers

Here we have given TN 11th Model Question Papers with Answers for all subjects in English Tamil Medium. Previous Year Question Papers and Model Papers will help students to know about their preparation level not only that these papers will also help Students to analyze about the repeated questions and important questions that are asked in previous year public examinations. As per the new exam pattern, there will be no change in the syllabus. Now students can get their Tamil Nadu 11th Model Question Papers of all Subjects in English Tamil Medium from the above list.

It is necessary that students will understand the new pattern and style of Model Question Papers of 11th Standard Tamilnadu State Board Syllabus according to the latest exam pattern. These Tamilnadu Plus One 11th Model Question Papers State Board Tamil Medium and English Medium are useful to understand the pattern of questions asked in the board exam. Know about the important concepts to be prepared for TN HSLC Board Exams and Score More marks.

We hope the given Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern Class 11th Model Question Papers 2020 2021 with Answers Pdf Free Download in English Medium and Tamil Medium will help you get through your subjective questions in the exam.

Let us know if you have any concerns regarding the Tamil Nadu Government 11th State Board Model Question Papers with Answers 2020 21 for All Subjects, TN 11th Std Public Exam Question Papers with Answer Key, New Paper Pattern of HSC Class 11th Previous Year Question Papers, Plus One +1 Model Sample Papers, Tamil Nadu 11th Quarterly Half Yearly Model Question Papers, drop a comment below and we will get back to you as soon as possible.

Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.1

Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.1 Text Book Back Questions and Answers

Question 1.
Convert the following degree measure into radian measure
(i) 60°
(ii) 150°
(iii) 240°
(iv) -320°
Solutions:
(i) 1°= \(\frac{\pi}{180}\) radians
∴ 60° = \(\frac{\pi}{180}\) × 60 radians = \(\frac{\pi}{3}\) radians.

(ii) 150° = \(\frac{\pi}{180}\) × 150 radians = \(\frac{5 \pi}{6}\) radians.

(iii) 240° = \(\frac{\pi}{180}\) × 240 radians = \(\frac{4 \pi}{3}\) radians.

(iv) -320° = \(\frac{\pi}{180}\) × -320 = \(\frac{-16 \pi}{9}\) radians

Question 2.
Find the degree measure corresponding to the following radian measure.
(i) \(\frac{\pi}{8}\)
(ii) \(\frac{9 \pi}{5}\)
(iii) -3
(iv) \(\frac{11 \pi}{18}\)
Solution:
We know that, one radian = \(\frac{180^{\circ}}{\pi}\)
(i) \(\frac{\pi}{8}\)
\(\frac{\pi}{8}=\frac{180^{\circ}}{\pi} \times \frac{\pi}{8}\) degrees
= \(\frac{45}{2}\)
= 22.5°
= 22°30′ [∵ 0.5° = (0.5 × 60)’ = 30′]

(ii) \(\frac{9 \pi}{5}\)
\(\frac{9 \pi}{5}=\frac{180^{\circ}}{\pi} \times \frac{9 \pi}{5}\) degrees
= 36 × 9 degrees
= 324°

(iii) -3

= -171.81°
= -171°48′ (∵ 0.8° = (0.8 × 60)’ = 48′)

(iv) \(\frac{11 \pi}{18}\)
\(\frac{11 \pi}{18}=\frac{180}{\pi} \times \frac{11 \pi}{18}\)
= 10 × 11°
= 110°

Question 3.
Determine the quadrants in which the following degree lie.
(i) 380°
(ii) -140°
(iii) 1195°
Solution:
(i) 380° = 360°+ 20°
This is of the form 360° + θ
∴ After one completion of the round, the angle is 20°, 380° lies in the I quadrant.

(ii) -140° = -90° + (-50°)
The angle is negative it moves in the anti-clockwise direction.
-140° lies in the III quadrants.

(iii) 1195° = (3 × 360°) + 90° + 25°
∴ After three completion round, the angle will lie in the II quadrant.
1195° lies in the II quadrant.

Question 4.
Find the values of each of the following trigonometric ratios.
(i) sin 300°
(ii) cos(-210°)
(iii) sec 390°
(iv) tan(-855°)
(v) cosec 1125°
Solution:
(i) sin 300° = sin(360° – 60°)
[For 360° – 60°. No change in T-ratio. 300° lies in 4th quadrant ‘sin’ is negative]
= -sin 60°
= \(-\frac{\sqrt{3}}{2}\)

(ii) cos(-210°) = cos 210° (∵ cos(-θ) = cos θ)
[∵ 180 + 30°. No change in T-ratio. 210° lies 3rd quadrant ‘cos’ is negative]
= cos(180° + 30°)
= -cos 30°
= \(-\frac{\sqrt{3}}{2}\)

(iii) sec 390° = sec(360° + 30°)
= sec 30°
= \(\frac{1}{\cos 30^{\circ}}\)
= \(\frac{1}{\left(\frac{\sqrt{3}}{2}\right)}\)
= \(\frac{2}{\sqrt{3}}\)

(iv) tan(-855°) = -tan 855° (∵ tan(-θ) = – tan θ)
[∵ Multiplies of 360° are dropped out. For 180° – 45°. No change in T-ratio. 180° – 45° lies in 2nd quadrant ‘tan’ is negative]
= -tan(2 × 360° + 135°)
= -tan 135°
= -tan(180° – 45°)
= -(-tan 45°)
= -(-1)
= 1

(v) cosec 1125° = cosec(3 × 360°+ 45°)
= cosec 45°
= \(\frac{1}{\sin 45^{\circ}}\)
= \(\frac{1}{\left(\frac{1}{\sqrt{2}}\right)}\)
= √2

Question 5.
Prove that:
(i) tan(-225°) cot(-405°) – tan(-765°) cot(675°) = 0.
(ii) 2 sin² \(\frac{\pi}{6}\) + cosec² \(\frac{7 \pi}{6}\) cos² \(\frac{\pi}{3}\) = \(\frac{3}{2}\)
(iii) \(\sec \left(\frac{3 \pi}{2}-\theta\right) \sec \left(\theta-\frac{5 \pi}{2}\right)+\tan \left(\frac{5 \pi}{2}+\theta\right) \tan \left(\theta-\frac{5 \pi}{2}\right)=-1\)
Solution:
(i) tan(-225°) = -(tan 225°)
= -(tan(180° + 45°))
= – tan 45°
= – 1
cot(-405°) = -(cot 405°)
= – cot(360° + 45°) [∵ For 360° + 45° no change in T-ratio.]
= -cot 45°
= -1
tan(-765°) = -tan 765°
= -tan(2 × 360° + 45°)
= -tan 45°
= -1
cot 675° = cot (360°+ 315°)
= cot 315°
= cot(360° – 45°)
= -cot 45°
= -1
LHS = tan(-225°) cot(-405°) – tan(-765°) cot(675°)
= (-1) (-1) – (-1) (-1)
= 1 – 1
= 0
= RHS.
Hence proved.

(ii) 2 sin² \(\frac{\pi}{6}\) + cosec² \(\frac{7 \pi}{6}\) cos² \(\frac{\pi}{3}\) = \(\frac{3}{2}\)
LHS = 2 sin² \(\frac{\pi}{6}\) + cosec² \(\frac{7 \pi}{6}\) cos² \(\frac{\pi}{3}\)
[∵ \(\frac{7 \pi}{6}\) = 210°, 210° = 180° + 30°. For 180° + 30° no change in T-ratio.
210° lies in 3rd quadrant, cosec θ is negative.]
= 2\(\left(\sin \frac{\pi}{6}\right)^{2}\) + (cosec (180° + 30°))² \(\left(\cos \frac{\pi}{3}\right)^{2}\)
= 2 \(\left(\frac{1}{2}\right)^{2}\) + (-cosec 30°)² . \(\left(\frac{1}{2}\right)^{2}\)
= \(2 \times \frac{1}{4}+(-2)^{2} \frac{1}{4}\)
= \(\frac{2}{4}+\frac{4}{4}=\frac{6}{4}\)
= \(\frac{6}{4}\)
= \(\frac{3}{2}\)
= RHS

(iii) sec(\(\frac{3 \pi}{2}\) – θ) = sec (270° – θ) = -cosec θ
[∵ For 270° – θ change T-ratio. So add ‘co’ infront ‘sec’, it becomes ‘cosec’]
sec(θ – \(\frac{5 \pi}{2}\)) = \(\sec \left(-\left(\frac{5 \pi}{2}-\theta\right)\right)\)
= sec(\(\frac{5 \pi}{2}\) – θ) [∵ sec(-θ) = θ]
= sec(450° – θ)
= sec (360° + (90° – θ))
= sec (90° – θ)
= cosec θ
[∵ For 90° – θ change in T-ratio. So add ‘co’ in front of ‘sec’ it becomes ‘cosec’]
tan(\(\frac{5 \pi}{2}\) + θ) = tan(450° + θ)
[∵ For 90° + θ, change in T-ratio. So add ‘co’ in front of ‘tan’ it becomes ‘cot’]
= tan (360° + (90° + θ))
= tan (90° + θ)
= -cot θ
\(\tan \left(\theta-\frac{5 \pi}{2}\right)=\tan \left(-\left(\frac{5 \pi}{2}-\theta\right)\right)\)
= \(-\tan \left(\frac{5 \pi}{2}-\theta\right)\) [∵ tan(-θ) = -tan θ]
= -tan(450° – θ)
= -tan(360° + (90° – θ))
= -tan(90° – θ)
= -cot θ
LHS = \(\sec \left(\frac{3 \pi}{2}-\theta\right) \sec \left(\theta-\frac{5 \pi}{2}\right)+\tan \left(\frac{5 \pi}{2}+\theta\right) \tan \left(\theta-\frac{5 \pi}{2}\right)\)
= -cosec θ (cosec θ) + (-cot θ) (-cot θ)
= -cosec² θ + cot² θ
= -(1 + cot² θ) + cot² θ [∵ 1 + cot² θ = cosec² θ]
= -1
= RHS

Question 6.
If A, B, C, D are angles of a cyclic quadrilateral, prove that: cos A + cos B + cos C + cos D = 0.
Solution:
Note: If the vertices of a quadrilateral lie on the circle then the quadrilateral is called a cyclic quadrilateral.
In a cyclic quadrilateral sum of opposite angles are 180°.

Since A, B, C, D are angles of cyclic quadrilateral
A + C = 180° and B + D = 180°
LHS = cos A + cos B + cos C + cos D
= cos A + cos B + cos(180° – A) + cos(180° – B)
= cos A + cos B – cos A – cos B
= 0
= RHS

Question 7.
Prove that

(ii) sin θ . cos{sin(\(\frac{\pi}{2}\) – θ) . cosec θ + cos(\(\frac{\pi}{2}\) – θ) . sec θ} = 1
Solution:

(ii) sin θ . cos{sin(\(\frac{\pi}{2}\) – θ) . cosec θ + cos(\(\frac{\pi}{2}\) – θ) . sec θ} = 1

Question 8.
Prove that: cos 510° cos 330° + sin 390° cos 120° = -1.
Solution:
LHS = cos 510° cos 330° + sin 390° cos 120°
= cos(360° + 150°) cos(360° – 30°) + sin(360° + 30°) × cos(180° – 60°)
= cos 150° cos 30° + sin 30° (-cos 60°)
= cos(180° – 30°) cos 30° + sin 30° cos 60°
= -cos 30° cos 30° + \(\frac{1}{2} \times\left(\frac{-1}{2}\right)\)
= \(-\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}-\frac{1}{2} \times \frac{1}{2}\)
= \(-\frac{3}{4}-\frac{1}{4}\)
= \(\frac{-3-1}{4}\)
= -1

Question 9.
Prove that:
(i) tan(π + x) cot(x – π) – cos(2π – x) cos(2π + x) = sin² x.

Solution:
(i) tan(π + x) cot(x – π) – cos(2π – x) cos(2π + x) = (tan x) (-cot(π – x) – cos x cos x
[∵ cot(x – π) = cot(-(π – x)) = -cot(π – x) = cot x]
= tan x cot x – cos² x
= 1 – cos² x
= sin² x [∵ sin² x + cos² x = 1 ⇒ sin² x = (1 – cos² x)]

Question 10.
If sin θ = \(\frac{3}{5}\), tan φ = \(\frac{1}{2}\) and \(\frac{\pi}{2}\) < θ < π < φ < \(\frac{3 \pi}{2}\), then find the value of 8 tan θ – √5 sec φ.
Solution:

Given that sin θ = \(\frac{3}{5}=\frac{\text { Opposite side }}{\text { Hypotenuse }}\)
∵ AB = \(\sqrt{5^{2}-3^{2}}=\sqrt{25-9}=\sqrt{16}\) = 4
Here θ lies in second quadrant [∵ \(\frac{\pi}{2}\) < θ < π]
∵ tan θ is negative.
tan θ = \(-\frac{3}{4}\)
Also given that tan Φ = \(\frac{1}{2}=\frac{\text { Opposite side }}{\text { Adjacent side }}\)
∴ PR = \(\sqrt{\mathrm{PQ}^{2}+\mathrm{QP}^{2}}=\sqrt{4+1}=\sqrt{5}\)
Here Φ lies in third quadrant (∵ π < Φ < \(\frac{3 \pi}{2}\))
∴ sec Φ is negative.
\(\sec \phi=\frac{1}{\cos \phi}=-\frac{1}{\left(\frac{2}{\sqrt{5}}\right)}=-\frac{\sqrt{5}}{2}\)
Now 8 tan θ – √5 sec Φ = \(8\left(-\frac{3}{4}\right)-\sqrt{5}\left(\frac{-\sqrt{5}}{2}\right)\)
= 2 × (-3) + \(\frac{5}{2}\)
= -6 + \(\frac{5}{2}\)
= \(\frac{-12+5}{2}\)
= \(\frac{-7}{2}\)

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.7 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.7

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.7 Text Book Back Questions and Answers

Question 1.
If m₁ and m₂ are the slopes of the pair of lines given by ax² + 2hxy + by² = 0, then the value of m₁ + m₂ is:
(a) \(\frac{2 h}{b}\)
(b) \(-\frac{2 h}{b}\)
(c) \(\frac{2 h}{a}\)
(d) \(-\frac{2 h}{a}\)
Answer:
(b) \(-\frac{2 h}{b}\)

Question 2.
The angle between the pair of straight lines x² – 7xy + 4y² = 0 is:
(a) \(\tan ^{-1}\left(\frac{1}{3}\right)\)
(b) \(\tan ^{-1}\left(\frac{1}{2}\right)\)
(c) \(\tan ^{-1}\left(\frac{\sqrt{33}}{5}\right)\)
(d) \(\tan ^{-1}\left(\frac{5}{\sqrt{33}}\right)\)
Answer:
(c) \(\tan ^{-1}\left(\frac{\sqrt{33}}{5}\right)\)
Hint:
x² – 7xy + 4y² = 0
Here 2h = -7, a = 1, b = 4

Question 3.
If the lines 2x – 3y – 5 = 0 and 3x – 4y – 7 = 0 are the diameters of a circle, then its centre is:
(a) (-1, 1)
(b) (1, 1)
(c) ( 1, -1)
(d) (-1, -1)
Answer:
(c) ( 1, -1)
Hint:
To get centre we must solve the given equations
2x – 3y – 5 = 0 …….(1)
3x – 4y – 7 = 0 ………(2)
(1) × 3 ⇒ 6x – 9y = 15
(2) × 2 ⇒ 6x – 8y = 14
Subtracting, -y = 1 ⇒ y = -1
Using y = -1 in (1) we get
2x + 3 – 5 = 0
⇒ 2x = 2
⇒ x = 1

Question 4.
The x-intercept of the straight line 3x + 2y – 1 = 0 is
(a) 3
(b) 2
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{3}\)
Hint:
To get x-intercept put y = 0 in 3x + 2y – 1 = 0 we get
3x – 1 = 0
x = \(\frac{1}{3}\)

Question 5.
The slope of the line 7x + 5y – 8 = 0 is:
(a) \(\frac{7}{5}\)
(b) \(-\frac{7}{5}\)
(c) \(\frac{5}{7}\)
(d) \(-\frac{5}{7}\)
Answer:
(b) \(-\frac{7}{5}\)
Hint:
Slope of 7x + 5y – 8 = 0 is = \(\frac{-x \text { coefficient }}{y \text { coefficient }}\) = \(-\frac{7}{5}\)

Question 6.
The locus of the point P which moves such that P is at equidistance from their coordinate axes is:
(a) y = \(\frac{1}{x}\)
(b) y = -x
(c) y = x
(d) y = \(\frac{-1}{x}\)
Answer:
(c) y = x
Hint:

Given PA = PB
y₁ = x₁
∴ Locus is y = x

Question 7.
The locus of the point P which moves such that P is always at equidistance from the line x + 2y + 7 = 0:
(a) x + 2y + 2 = 0
(b) x – 2y + 1 = 0
(c) 2x – y + 2 = 0
(d) 3x + y + 1 = 0
Answer:
(a) x + 2y + 2 = 0
Hint:
Locus is line parallel to line x + 2y + 7 = 0 which is x + 2y + 2 = 0

Question 8.
If kx² + 3xy – 2y² = 0 represent a pair of lines which are perpendicular then k is equal to:
(a) \(\frac{1}{2}\)
(b) \(-\frac{1}{2}\)
(c) 2
(d) -2
Answer:
(c) 2
Hint:
Here a = k, b = -2
Condition for perpendicular is
a + b = 0
⇒ k – 2 = 0
⇒ k = 2

Question 9.
(1, -2) is the centre of the circle x² + y² + ax + by – 4 = 0, then its radius:
(a) 3
(b) 2
(c) 4
(d) 1
Answer:
(a) 3
Hint:
Given centre (-g, -f) = (1, -2)
From the given equation c = -4
Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-(-4)}=\sqrt{9}\) = 3

Question 10.
The length of the tangent from (4, 5) to the circle x² + y² = 16 is:
(a) 4
(b) 5
(c) 16
(d) 25
Answer:
(b) 5
Hint:
Length of the tangent from (x₁, y₁) to the circle x² + y² = 16 is \(\sqrt{x_{1}^{2}+y_{1}^{2}-16}=5\)

Question 11.
The focus of the parabola x² = 16y is:
(a) (4 , 0)
(b) (-4, 0)
(c) (0, 4)
(d) (0, -4)
Answer:
(c) (0, 4)
Hint:
x² = 16y
Here 4a = 16 ⇒ a = 4
Focus is (0, a) = (0, 4)

Question 12.
Length of the latus rectum of the parabola y² = -25x:
(a) 25
(b) -5
(c) 5
(d) -25
Answer:
(a) 25
Hint:
y² = -25a
Here 4a = 25 which is the length of the latus rectum.

Question 13.
The centre of the circle x² + y² – 2x + 2y – 9 = 0 is:
(a) (1, 1)
(b) (-1, 1)
(c) (-1, 1)
(d) (1, -1)
Answer:
(d) (1, -1)
Hint:
2g = -2, 2f = 2
g = -1, f = 1
Centre = (-g, -f) = (1, -1)

Question 14.
The equation of the circle with centre on the x axis and passing through the origin is:
(a) x² – 2ax + y² = 0
(b) y² – 2ay + x² = 0
(c) x² + y² = a²
(d) x² – 2ay + y² = 0
Answer:
(a) x² – 2ax + y² = 0
Hint:
Let the centre on the x-axis as (a, 0).
This circle passing through the origin so the radius

Now centre (h, k) = (a, 0)
Radius = a
Equation of the circle is (x – a)² + (y – 0)² = a²
⇒ x² – 2ax + a² + y² = a²
⇒ x² – 2ax + y² = 0

Question 15.
If the centre of the circle is (-a, -b) and radius is \(\sqrt{a^{2}-b^{2}}\) then the equation of circle is:
(a) x² + y² + 2ax + 2by + 2b² = 0
(b) x² + y² + 2ax + 2by – 2b² = 0
(c) x² + y² – 2ax – 2by – 2b² = 0
(d) x² + y² – 2ax – 2by + 2b² = 0
Answer:
(a) x² + y² + 2ax + 2by + 2b² = 0
Hint:
Equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x + a)² + (y + b)² = a² – b²
⇒ x² + y² + 2ax + 2by + a² + b² = a² – b²
⇒ x² + y² + 2ax + 2by + 2b² = 0

Question 16.
Combined equation of co-ordinate axes is:
(a) x² – y² = 0
(b) x² + y² = 0
(c) xy = c
(d) xy = 0
Answer:
(d) xy = 0
Hint:
Equation of x-axis is y = 0
Equation of y-axis is x = 0
Combine equation is xy = 0

Question 17.
ax² + 4xy + 2y² = 0 represents a pair of parallel lines then ‘a’ is:
(a) 2
(b) -2
(c) 4
(d) -4
Answer:
(a) 2
Hint:
Here a = 0, h = 2, b = 2
Condition for pair of parallel lines is b² – ab = 0
4 – a(2) = 0
⇒ -2a = -4
⇒ a = 2

Question 18.
In the equation of the circle x² + y² = 16 then v intercept is (are):
(a) 4
(b) 16
(c) ±4
(d) ±16
Answer:
(c) ±4
Hint:
To get y-intercept put x = 0 in the circle equation we get
0 + y² = 16
∴ y = ±4

Question 19.
If the perimeter of the circle is 8π units and centre is (2, 2) then the equation of the circle is:
(a) (x – 2)² + (y – 2)² = 4
(b) (x – 2)² + (y – 2)² = 16
(c) (x – 4)² + (y – 4)² = 16
(d) x² + y² = 4
Answer:
(c) (x – 2)² + (y – 2)² = 16
Hint:
Perimeter, 2πr = 8π
r = 4
Centre is (2, 2)
Equation of the circle is (x – 2)² + (y – 2)² = 4² = 16

Question 20.
The equation of the circle with centre (3, -4) and touches the x-axis is:
(a) (x – 3)² + (y – 4)² = 4
(b) (x – 3)² + (y + 4)² = 16
(c) (x – 3)² + (y – 4)² = 16
(d) x² + y² = 16
Answer:
(b) (x – 3)² + (y + 4)² = 16
Hint:
Centre (3, -4).
It touches the x-axis.
The absolute value of y-coordinate is the radius, i.e., radius = 4.
Equation is (x – 3)² + (y + 4)² = 16

Question 21.
If the circle touches the x-axis, y-axis, and the line x = 6 then the length of the diameter of the circle is:
(a) 6
(b) 3
(c) 12
(d) 4
Answer:
(a) 6
Hint:

Question 22.
The eccentricity of the parabola is:
(a) 3
(b) 2
(c) 0
(d) 1
Answer:
(d) 1

Question 23.
The double ordinate passing through the focus is:
(a) focal chord
(b) latus rectum
(c) directrix
(d) axis
Answer:
(b) latus rectum
Hint:

Question 24.
The distance between directrix and focus of a parabola y² = 4ax is:
(a) a
(b) 2a
(c) 4a
(d) 3a
Answer:
(b) 2a

Question 25.
The equation of directrix of the parabola y² = -x is:
(a) 4x + 1 = 0
(b) 4x – 1 = 0
(c) x – 1 = 0
(d) x + 4 = 0
Answer:
(b) 4x – 1 = 0
Hint:
y² = -x.
It is a parabola open leftwards.
Here 4a = 1 ⇒ a = \(\frac{1}{4}\)
Equation of directrix is x = a.
i.e., x = \(\frac{1}{4}\) (or) 4x – 1 = 0

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.6 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.6

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.6 Text Book Back Questions and Answers

Question 1.
Find the equation of the parabola whose focus is the point F(-1, -2) and the directrix is the line 4x – 3y + 2 = 0.
Solution:
F(-1, -2)
l : 4x – 3y + 2 = 0
Let P(x, y) be any point on the parabola.
FP = PM
⇒ FP² = PM²
⇒ (x + 1)² + (y + 2)² = \(\left[\frac{4 x-3 y+2}{\sqrt{4^{2}+(-3)^{2}}}\right]^{2}\)
⇒ x² + 2x + 1 + y² + 4y + 4 = \(\frac{16 x^{2}+9 y^{2}+4-24 x y+16 x-12 y}{(16+9)}\)
⇒ 25(x² + y² + 2x + 4y + 5) = 16x² + 9y² – 24xy + 16x – 12y + 4
⇒ (25 – 16)x² + (25 – 9)y² + 24xy + (50 – 16)x + (100 + 12)y + 125 – 4 = 0
⇒ 9x² + 16y² + 24xy + 34x + 112y + 121 = 0

Question 2.
The parabola y² = kx passes through the point (4, -2). Find its latus rectum and focus.
Solution:
y² = kx passes through (4, -2)
(-2)² = k(4)
⇒ 4 = 4k
⇒ k = 1
y² = x = 4(\(\frac{1}{4}\))x
a = \(\frac{1}{4}\)
Equation of LR is x = a or x – a = 0
i.e., x = \(\frac{1}{4}\)
⇒ 4x = 1
⇒ 4x – 1 = 0
Focus (a, 0) = (\(\frac{1}{4}\), 0)

Question 3.
Find the vertex, focus, axis, directrix, and the length of the latus rectum of the parabola y² – 8y – 8x + 24 = 0.
Solution:
y² – 8y – 8x + 24 = 0
⇒ y² – 8y – 4² = 8x – 24 + 4²
⇒ (y – 4)² = 8x – 8
⇒ (y – 4)² = 8(x – 1)
⇒ (y – 4)² = 4(2) (x – 1)
∴ a = 2
Y² = 4(2)X where X = x – 1 and Y = y – 4

Question 4.
Find the co-ordinates of the focus, vertex, equation of the directrix, axis and the length of latus rectum of the parabola (a) y² = 20x, (b) x² = 8y, (c) x² = -16y
Solution:
(a) y² = 20x
y² = 4(5)x
∴ a = 5

(b) x² = 8y = 4(2)y
∴ a = 2

(c) x² = -16y = -4(4)y
∴ a = 4

Question 5.
The average variable cost of the monthly output of x tonnes of a firm producing a valuable metal is ₹ \(\frac{1}{5}\) x² – 6x + 100. Show that the average variable cost curve is a parabola. Also, find the output and the average cost at the vertex of the parabola.
Solution:
Let output be x and average variable cost = y
y = \(\frac{1}{5}\) x² – 6x + 100
⇒ 5y = x² – 30x + 500
⇒ x² – 30x + 225 = 5y – 500 + 225
⇒ (x – 15)² = 5y – 275
⇒ (x – 15)² = 5(y – 55) which is of the form X² = 4(\(\frac{5}{4}\))Y
∴ Y average variable cost curve is a parabola
Vertex (0, 0)
x – 15 = 0; y – 55 = 0
x = 15; y = 55
At the vertex, output is 15 tonnes and average cost is ₹ 55.

Question 6.
The profit ₹ y accumulated in thousand in x months is given by y = -x² + 10x – 15. Find the best time to end the project.
Solution:
y = -x² + 10x – 15
⇒ y = -[x² – 10x + 5² – 5² + 15]
⇒ y = -[(x – 5)² – 10]
⇒ y = 10 – (x – 5)²
⇒ (x – 5)² = -(y – 10)
This is a parabola which is open downwards.
Vertex is the maximum point.
∴ Profit is maximum when x – 5 = 0 (or) x = 5 months.
After that profit gradually reduces.
∴ The best time to end the project is after 5 months.

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.5 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.5

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.5 Text Book Back Questions and Answers

Question 1.
Find the equation of the tangent to the circle x² + y² – 4x + 4y – 8 = 0 at (-2, -2).
Solution:
The equation of the tangent to the circle x² + y² – 4x + 4y – 8 = 0 at (x₁, y₁) is
xx₁ + yy₁ – 4\(\frac{\left(x+x_{1}\right)}{2}\) + 4\(\frac{\left(y+y_{1}\right)}{2}\) – 8 = 0
Here (x₁, y₁) = (-2, -2)
⇒ x(-2) + y(-2) – 2(x – 2) + 2(y – 2) – 8 = 0
⇒ -2x – 2y – 2x + 4 + 2y – 4 – 8 = 0
⇒ -4x – 8 = 0
⇒ x + 2 = 0

Question 2.
Determine whether the points P(1, 0), Q(2, 1) and R(2, 3) lie outside the circle, on the circle or inside the circle x² + y² – 4x – 6y + 9 = 0.
Solution:
The equation of the circle is x² + y² – 4x – 6y + 9 = 0
PT² = \(x_{1}^{2}+y_{1}^{2}\) – 4x₁ – 6y₁ + 9
At P(1, 0), PT² = 1 + 0 – 4 – 0 + 9 = 6 > 0
At Q(2, 1), PT² = 4 + 1 – 8 – 6 + 9 = 0
At R(2, 3), PT² = 4 + 9 – 8 – 18 + 9 = -4 < 0
The point P lies outside the circle.
The point Q lies on the circle.
The point R lies inside the circle.

Question 3.
Find the length of the tangent from (1, 2) to the circle x² + y² – 2x + 4y + 9 = 0.
Solution:
The length of the tangent from (x₁, y₁) to the circle x² + y² – 2x + 4y + 9 = 0 is \(\sqrt{x_{1}^{2}+y_{1}^{2}-2 x_{1}+4 y_{1}+9}\)
Length of the tangent from (1, 2) = \(\sqrt{1^{2}+2^{2}-2(1)+4(2)+9}\)
= \(\sqrt{1+4-2+8+9}\)
= \(\sqrt{20}\)
= \(\sqrt{4 \times 5}\)
= 2√5 units

Question 4.
Find the value of P if the line 3x + 4y – P = 0 is a tangent to the circle x² + y² = 16.
Solution:
The condition for a line y = mx + c to be a tangent to the circle x² + y² = a² is c² = a² (1 + m²)
Equation of the line is 3x + 4y – P = 0
Equation of the circle is x² + y² = 16
4y = -3x + P
y = \(\frac{-3}{4} x+\frac{P}{4}\)
∴ m = \(\frac{-3}{4}\), c = \(\frac{P}{4}\)
Equation of the circle is x² + y² = 16
∴ a² = 16
Condition for tangency we have c² = a²(1 + m²)
⇒ \(\left(\frac{P}{4}\right)^{2}=16\left(1+\frac{9}{16}\right)\)
⇒ \(\frac{P^{2}}{16}=16\left(\frac{25}{16}\right)\)
⇒ P² = 16 × 25
⇒ P = ±√16√25
⇒ P = ±4 × 5
⇒ P = ±20

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.4 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.4

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.4 Text Book Back Questions and Answers

Question 1.
Find the equation of the following circles having
(i) the centre (3, 5) and radius 5 units.
(ii) the centre (0, 0) and radius 2 units.
Solution:
(i) Equation of the circle is (x – h)² + (y – k)² = r²
Centre (h, k) = (3, 5) and radius r = 5
∴ Equation of the circle is (x – 3)² + (y – 5)² = 5²
⇒ x² – 6x + 9 + y² – 10y + 25 = 25
⇒ x² + y² – 6x – 10y + 9 = 0

(ii) Equation of the circle when centre origin (0, 0) and radius r is x² + y² = r²
⇒ x² + y² = 2²
⇒ x² + y² = 4
⇒ x² + y² – 4 = 0

Question 2.
Find the centre and radius of the circle
(i) x² + y² = 16
(ii) x² + y² – 22x – 4y + 25 = 0
(iii) 5x² + 5y²+ 4x – 8y – 16 = 0
(iv) (x + 2) (x – 5) + (y – 2) (y – 1) = 0
Solution:
(i) x² + y² = 16
⇒ x² + y² = 4²
This is a circle whose centre is origin (0, 0), radius 4.

(ii) Comparing x² + y² – 22x – 4y + 25 = 0 with general equation of circle x² + y² + 2gx + 2fy + c = 0
We get 2g = -22, 2f = -4, c = 25
g = -11, f = -2, c = 25
Centre = (-g, -f) = (11, 2)

(iii) 5x² + 5y² + 4x – 8y – 16 = 0
To make coefficient of x² unity, divide the equation by 5 we get,
\(x^{2}+y^{2}+\frac{4}{5} x-\frac{8}{5} y-\frac{16}{5}=0\)
Comparing the above equation with x² + y² + 2gx + 2fy + c = 0 we get,

(iv) Equation of the circle is (x + 2) (x – 5) + (y – 2) (y – 1) = 0
x² – 3x – 10 + y² – 3y + 2 = 0
x² + y² – 3x – 3y – 8 = 0
Comparing this with x² + y² + 2gx + 2fy + c = 0
We get 2g = -3, 2f = -3, c = -8
g = \(\frac{-3}{2}\), f = \(\frac{-3}{2}\), c = -8
Centre (-g, -f) = \(\left(\frac{3}{2}, \frac{3}{2}\right)\)

Question 3.
Find the equation of the circle whose centre is (-3, -2) and having circumference 16π.
Solution:
Circumference, 2πr = 16π
⇒ 2r = 16
⇒ r = 8
Equation of the circle when centre and radius are known is (x – h)² + (y – k)² = r²
⇒ (x + 3)² + (y + 2)² = 8²
⇒ x² + 6x + 9 + y² + 4y + 4 = 64
⇒ x² + y² + 6x + 4y + 13 = 64
⇒ x² + y² + 6x + 4y – 51 = 0

Question 4.
Find the equation of the circle whose centre is (2, 3) and which passes through (1, 4).
Solution:

Centre (h, k) = (2, 3)

Equation of the circle with centre (h, k) and radius r is (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = (√2)²
⇒ x² – 4x + 4 + y² – 6y + 9 = 2
⇒ x² + y² – 4x – 6y + 11 = 0

Question 5.
Find the equation of the circle passing through the points (0, 1), (4, 3) and (1, -1).
Solution:
Let the required of the circle be x² + y² + 2gx + 2fy + c = 0 ……… (1)
It passes through (0, 1)
0 + 1 + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 …….. (2)
Again the circle (1) passes through (4, 3)
4² + 3² + 2g(4) + 2f(3) + c = 0
16 + 9 + 8g + 6f + c = 0
8g + 6f + c = -25 …….. (3)
Again the circle (1) passes through (1, -1)
1² + (-1)² + 2g(1) + 2f(-1) + c = 0
1 + 1 + 2g – 2f + c = 0
2g – 2f + c = -2 ……… (4)
8g + 6f + c = -25
(4) × 4 subtracting we get, 8g – 8f + 4c = -8
14f – 3c = -17 ………. (5)
14f – 3c = -17
(2) × 3 ⇒ 6f + 3c = -3
Adding we get 20f = -20
f = -1
Using f = -1 in (2) we get, 2(-1) + c = -1
c = -1 + 2
c = 1
Using f = -1, c = 1 in (3) we get
8g + 6(-1)+1 = -25
8g – 6 + 1 = -25
8g – 5 = -25
8g = -20
g = \(\frac{-20}{8}=\frac{-5}{2}\)
using g = \(\frac{-5}{2}\), f = -1, c = 1 in (1) we get the equation of the circle.
x² + y² + 2(\(\frac{-5}{2}\))x + 2(-1)y + 1 = 0
x² + y² – 5x – 2y + 1 = 0

Question 6.
Find the equation of the circle on the line joining the points (1, 0), (0, 1), and having its centre on the line x + y = 1.
Solution:

Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 ……… (1)
The circle passes through (1, 0)
1² + 0² + 2g(1) + 2f(0) + c = 0
1 + 2g + c = 0
2g + c = 1 …….. (2)
Again the circle (1) passes through (0, 1)
0² + 1² + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 ……. (3)
(2) – (3) gives 2g – 2f = 0 (or) g – f = 0 ………. (4)
Given that the centre of the circle (-g, -f) lies on the line x + y = 1
-g – f = 1 …….. (5)
(4) + (5) gives -2f = 1 ⇒ f = \(-\frac{1}{2}\)
Using f = \(-\frac{1}{2}\) in (5) we get
-g – (\(-\frac{1}{2}\)) = 1
-g = 1 – \(-\frac{1}{2}\) = \(\frac{1}{2}\)
g = \(-\frac{1}{2}\)
Using g = \(-\frac{1}{2}\) in (2) we get
2(\(-\frac{1}{2}\)) + c = -1
-1 + c = -1
c = 0
using g = \(-\frac{1}{2}\), f = \(-\frac{1}{2}\), c = 0 in (1) we get the equation of the circle,
x² + y² + 2(\(-\frac{1}{2}\))x + 2(\(-\frac{1}{2}\))y + 0 = 0
x² + y² – x – y = 0

Question 7.
If the lines x + y = 6 and x + 2y = 4 are diameters of the circle, and the circle passes through the point (2, 6) then find its equation.
Solution:
To get coordinates of centre we should solve the equations of the diameters x + y = 6, x + 2y = 4.
x + y = 6 ……. (1)
x + 2y = 4 ………. (2)
(1) – (2) ⇒ -y = 2
y = -2
Using y = -2 in (1) we get x – 2 = 6
x = 8
Centre is (8, -2) the circle passes through the point (2, 6).

Equation of the circle with centre (h, k) and radius r is (x – h)² + (y – k)² = r²
⇒ (x – 8)² + (y + 2)² = 10²
⇒ x² + y² – 16x + 4y + 64 + 4 = 100
⇒ x² + y² – 16x + 4y – 32 = 0

Question 8.
Find the equation of the circle having (4, 7) and (-2, 5) as the extremities of a diameter.
Solution:
The equation of the circle when entremities (x₁, y₁) and (x₂, y₂) are given is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 4) (x + 2) + (y – 7) (y – 5) = 0
⇒ x² – 2x – 8 + y² – 12y + 35 = 0
⇒ x² + y² – 2x – 12y + 27 = 0

Question 9.
Find the Cartesian equation of the circle whose parametric equations are x = 3 cos θ, y = 3 sin θ, 0 ≤ θ ≤ 2π.
Solution:
Given x = 3 cos θ, y = 3 sin θ
Now x² + y² = 9 cos²θ + 9 sin²θ
x² + y² = 9 (cos²θ + sin²θ)
x² + y² = 9 which is the Cartesian equation of the required circle.

Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.3

Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.3 Text Book Back Questions and Answers

Question 1.
If the equation ax² + 5xy – 6y² + 12x + 5y + c = 0 represents a pair of perpendicular straight lines, find a and c.
Solution:
Comparing ax² + 5xy – 6y² + 12x + 5y + c = 0 with ax² + 2hxy + by² + 2gx + 2fy + c = 0
We get a = a, 2h = 5, (or) h = \(\frac{5}{2}\), b = -6, 2g = 12 (or) g = 6, 2f = 5 (or) f = \(\frac{5}{2}\), c = c
Condition for pair of straight lines to be perpendicular is a + b = 0
a + (-6) = 0
a = 6
Next to find c. Condition for the given equation to represent a pair of straight lines is

R₁ → R₁ – R₃
Expanding along first row we get 0 – 0 + (6 – c) [\(\frac{25}{4}\) + 36] = 0
(6-c) [\(\frac{25}{4}\) + 36] = 0
6 – c = 0
6 = c (or) c = 6

Question 2.
Show that the equation 12x² – 10xy + 2y² + 14x – 5y + 2 = 0 represents a pair of straight lines and also find the separate equations of the straight lines.
Solution:
Comparing 12x² – 10xy + 2y² + 14x – 5y + 2 = 0 with ax² + 2hxy + by² + 2gh + 2fy + c = 0
We get a = 12, 2h = -10, (or) h = -5, b = 2, 2g = 14 (or) g = 7, 2f = -5 (or) f = \(-\frac{5}{2}\), c = 2
Condition for the given equation to represent a pair of straight lines is \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=0\)
\(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
12 & -5 & 7 \\
-5 & 2 & \frac{-5}{2} \\
7 & \frac{-5}{2} & 2
\end{array}\right|\)

= \(\frac{1}{4}\) [12(16 – 25) + 5(-40 + 70) + 7(50 – 56)]
= \(\frac{1}{4}\) [12(-9) + 5(30) + 7(-6)]
= \(\frac{1}{4}\) [-108 + 150 – 42]
= \(\frac{1}{4}\) [0]
= 0
∴ The given equation represents a pair of straight lines.
Consider 12x² – 10xy + 2y² = 2[6x² – 5xy + y²] = 2[(3x – y)(2x – y)] = (6x – 2y)(2x – y)
Let the separate equations be 6x – 2y + l = 0, 2x – y + m = 0
To find l, m
Let 12x² – 10xy + 2y² + 14x – 5y + 2 = (6x – 2y + l) (2x – y + m) ……. (1)
Equating coefficient of y on both sides of (1) we get
2l + 6m = 14 (or) l + 3m = 7 ………… (2)
Equating coefficient of x on both sides of (1) we get
-l – 2m = -5 ……… (3)
(2) + (3) ⇒ m = 2
Using m = 2 in (2) we get
l + 3(2) = 7
l = 7 – 6
l = 1
∴ The separate equations are 6x – 2y + 1 = 0, 2x – y + 2 = 0.

Question 3.
Show that the pair of straight lines 4x² + 12xy + 9y² – 6x – 9y + 2 = 0 represents two parallel straight lines and also find the separate equations of the straight lines.
Solution:
The given equation is 4x² + 12xy + 9y² – 6x – 9y + 2 = 0
Here a = 4, 2h = 12, (or) h = 6 and b = 9
h² – ab = 6² – 4 × 9 = 36 – 36 = 0
∴ The given equation represents a pair of parallel straight lines
Consider 4x² + 12xy + 9y² = (2x)² + 12xy + (3y)²
= (2x)² + 2(2x)(3y) + (3y)²
= (2x + 3y)²
Here we have repeated factors.
Now consider, 4x² + 12xy + 9y² – 6x – 9y + 2 = 0
(2x + 3y)² – 3(2x + 3y) + 2 = 0
t² – 3t + 2 = 0 where t = 2x + 3y
(t – 1)(t – 2) = 0
(2x + 3y – 1) (2x + 3y – 2) = 0
∴ Separate equations are 2x + 3y – 1 = 0, 2x + 3y – 2 = 0

Question 4.
Find the angle between the pair of straight lines 3x² – 5xy – 2y² + 17x + y + 10 = 0.
Solution:
The given equation is 3x² – 5xy – 2y² + 17x + y + 10 = 0
Here a = 3, 2h = -5, b = -2
If θ is the angle between the given straight lines then

Subject Matter Experts at SamacheerKalvi.Guide have created Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern 11th Maths Model Question Papers 2020-2021 with Answers Pdf Free Download in English Medium and Tamil Medium of TN 11th Standard Maths Public Exam Question Papers Answer Key, New Paper Pattern of HSC 11th Class Maths Previous Year Question Papers, Plus One +1 Maths Model Sample Papers are part of Tamil Nadu 11th Model Question Papers.

Let us look at these Government of Tamil Nadu State Board 11th Maths Model Question Papers Tamil Medium with Answers 2020-21 Pdf. Students can view or download the Class 11th Maths New Model Question Papers 2021 Tamil Nadu English Medium Pdf for their upcoming Tamil Nadu HSC Board Exams. Students can also read Tamilnadu Samcheer Kalvi 11th Maths Guide.

TN State Board 11th Maths Model Question Papers 2020 2021 English Tamil Medium

Tamil Nadu 11th Maths Model Question Papers English Medium 2020-2021

• Tamil Nadu 11th Maths Model Question Paper 1 English Medium
• Tamil Nadu 11th Maths Model Question Paper 2 English Medium
• Tamil Nadu 11th Maths Model Question Paper 3 English Medium
• Tamil Nadu 11th Maths Model Question Paper 4 English Medium
• Tamil Nadu 11th Maths Model Question Paper 5 English Medium

Tamil Nadu 11th Maths Model Question Papers Tamil Medium 2019-2020

• Tamil Nadu 11th Maths Model Question Paper 1 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 2 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 3 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 4 Tamil Medium
• Tamil Nadu 11th Maths Model Question Paper 5 Tamil Medium

11th Maths Model Question Paper Design 2020-2021 Tamil Nadu

Tamil Nadu 11th Maths Model Question Paper Weightage of Marks

It is necessary that students will understand the new pattern and style of Model Question Papers of 11th Standard Maths Tamilnadu State Board Syllabus according to the latest exam pattern. These Tamil Nadu Plus One 11th Maths Model Question Papers State Board Tamil Medium and English Medium are useful to understand the pattern of questions asked in the board exam. Know about the important concepts to be prepared for TN HSLC Board Exams and Score More marks.

We hope the given Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern Class 11th Maths Model Question Papers 2020 2021 with Answers Pdf Free Download in English Medium and Tamil Medium will help you get through your subjective questions in the exam.

Let us know if you have any concerns regarding the Tamil Nadu Government 11th Maths State Board Model Question Papers with Answers 2020 21, TN 11th Std Maths Public Exam Question Papers with Answer Key, New Paper Pattern of HSC Class 11th Maths Previous Year Question Papers, Plus One +1 Maths Model Sample Papers, drop a comment below and we will get back to you as soon as possible.