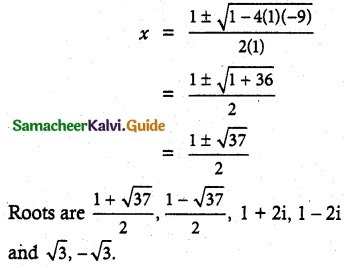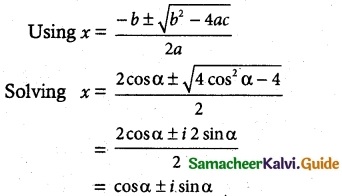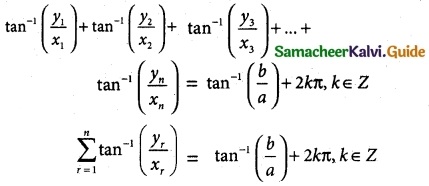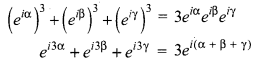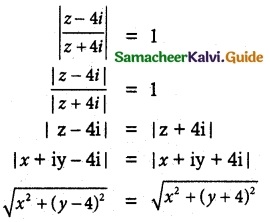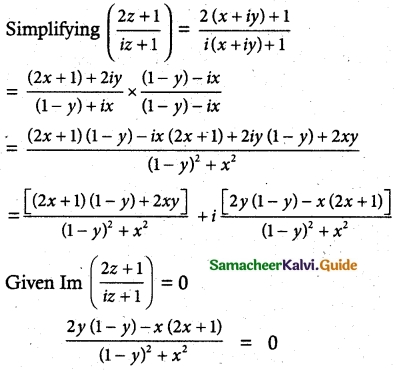Category: Class 12

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.5

Question 1.
Solve the following equations
(i) sin² x – 5 sin x + 4 = 0
Solution:
sin²x – 5sinx + 4 = 0
Let y = sin x
(y² – 5y + 4 = 0
(y – 1) (y – 4) = 0
(y – 1) = o or (y – 4) = 0
y = 1 or y = 4
sin x = 1 or sin x = 4 [not possible since sin x ≤ 1]
sin x = sin \(\frac{\pi}{2}\)
x = nπ + (-1)ⁿ α, n ∈ z.
x = nπ + (-1)ⁿ \(\frac{\pi}{2}\)

(ii) 12x³ + 8x = 29x² – 4 = 0
Solution:
12x³ – 29x² + 8x + 4 = 0

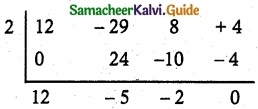
12x² – 5x – 2 = 0
12x² – 8x + 3x – 2 = 0
4x(3x – 2) + 1(3x – 2) = 0
(3x – 2)(4x + 1) = 0
3x = 2, 4x = -1
x = \(\frac{2}{3}\) or x = –\(\frac{1}{4}\)
The roots are 2, \(\frac{2}{3}\), –\(\frac{1}{4}\).

Question 2.
Examine for the rational roots of
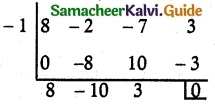
(i) 2x³ – x² – 1 = 0
Solution:
Sum of co-efficients = 2 – 1 – 1 = 0
⇒ x = 1 is a factor.

Which is imaginary root
∴ x = 1 is rational root.

(ii) x⁸ – 3x + 1 = 0
Solution:
a_n = 1; a₀ = 1
If \(\frac{p}{q}\) is a root of the polynomial. (p, q) = 1
By rational root theorem, it has no rational roots.

Question 3.
Solve: 8x^{\(\frac{3}{2n}\)} – 8x^{\(\frac{-3}{2n}\)} = 63.
Solution:
Put k = \(\frac{3}{2n}\) ∴ 8x^k – 8x^-k = 63
8x^k – \(\frac{8}{x^k}\) = 63
8x^2k – 8 = 63x^k
8x^2k – 63x^k – 8 = 0
(x^k – 8) (8x^k + 1) = 0
x^k – 8 = 0
x^k = 8
x^{\(\frac{3}{2n}\)} = 8
x = 8^{\(\frac{3}{2n}\)} (2³)^{\(\frac{3}{2n}\)} = (2²)ⁿ = 4ⁿ
∴ x = 4ⁿ is a root of the equation.

Question 4.
Solve: 2\(\sqrt{\frac{x}{a}}\) + 3\(\sqrt{\frac{a}{x}}\) = \(\frac{b}{a}\) = \(\frac{6a}{b}\)
Solution:
put \(\sqrt{\frac{x}{a}}\) = y

Question 5.
Solve the equations
(i) 6x⁴ – 35x³ + 62x² – 35x + 6 = 0
Solution:
This is Type I even degree reciprocal equation. Hence it can be rewritten as

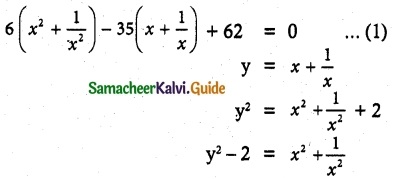
(1) ⇒ 6(y² – 2) – 35y + 62 = 0
6y² – 12 – 35y + 62 = 0
6y² – 35y + 50 = 0

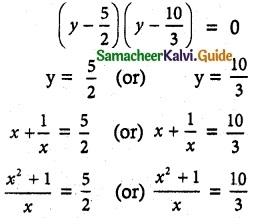
2x² + 2 – 5x = 0 (or) 3x² + 3 = 10x
2x² – 5x + 2 = 0 (or) 3x² – 10x + 3 = 0
x = 2, \(\frac{1}{2}\) (or) x = 3, \(\frac{1}{3}\)
Roots are 2, \(\frac{1}{2}\), 3 and \(\frac{1}{3}\)

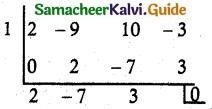
(ii) x⁴ + 3x³ – 3x – 1 = 0
Solution:
(x – 1) and (x + 1) is a factor.

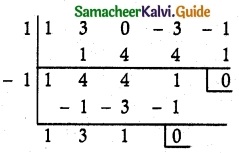
(x – 1)(x + 1)(x² + 3x + 1) = 0
x – 1 = 0 (or) x + 1 = 0 (or) x² + 3x + 1 = 0
x = 1 (or) x = -1 (or) x² + 3x = -1

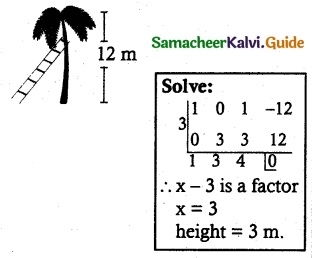
Question 6.
Find all real numbers satisfying
Solution:
4^x – 3 (2^x+2) + 2⁵ = 0
⇒ (2²)^x – 3(2^x . 2²) + 2⁵ = 0
(2²)^x – 12 . 2^x+ 32 = 0
Let y = 2^x
y² – 12y + 32 = 0
⇒ (y – 4) (y – 8) = 0
y – 4 = 0 or y – 8 = 0
Case (i): 2^x = 4
⇒ 2^x = (2)²
⇒ x = 2
Case (ii): 2x = 8
⇒ 2^x = (2)³
⇒ x = 3
∴ The roots are 2, 3

Question 7.
Solve the equation 6x⁴ – 5x³ – 38x² – 5x + 6 = 0 if it is known that \(\frac{1}{3}\) is a solution.
Solution:
6x⁴ – 5x³ – 38x² – 5x + 6 = 0

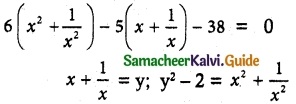
6(y² – 2) – 5y – 38 = 0
6y² – 12 – 5y – 38 = 0
6y² – 5y – 50 = 0
6y² – 20y + 15y  – 50 = 0
2y(3y – 10) + 5(3y – 10) = 0
(3y – 10)(2y + 5) = 0
3y = 10, 2y = -5

3x² + 3 = 10x, 2x² + 2 = -5x
3x² – 10x + 3 = 0, 2x² + 5x + 2 = 0
(x – 3)(3x – 1) = 0, (2x + 1)(x + 1) = 0
x = 3, x = \(\frac{1}{3}\) or x = \(\frac{-1}{2}\), x= -2
The roots are 3, \(\frac{1}{3}\), -2, \(\frac{-1}{2}\).

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.6

Question 1.
Discuss the maximum possible number of positive and negative roots of the polynomial equation 9x⁹ – 4x⁸ + 4x⁷ – 3x⁶ + 2x⁵ + x³ + 7x² + 7x + 2 = 0.
Solution:
P(x) = 9x⁹ – 4x⁸ + 4x⁷ – 3x⁶ + 2x⁵ + x³ + 7x² + 7x + 2
The number of sign changes in P(x) is 4.
∴P(x) has at most 4 positive roots.
P(-x) = -9x⁹ – 4x⁸ – 4x⁷ – 3x⁶ – 2x⁵ – x³ + 7x² – 7x + 2
The number of sign changes in P(-x) is 3.
P(x) has almost 3 negative roots.
Since the difference between the number of sign changes in co-efficient P(-x) and the number of negative roots of the polynomial P(x) is even.
The number of negative roots = at most 2.

Question 2.
Discuss the maximum possible number of positive and negative roots of the polynomial equations x² – 5x + 6 and x² – 5x + 16 . Also, draw a rough sketch of the graphs.
Solution:
y = x² – 5x + 6
x = 1, y = 1 – 5 + 6 = 2
x = 2, y = 4 – 10 + 6 = 0
x = 0, y = 6
x = 3, y = 9 – 15 + 6 = 0
x = -1, y = 1 + 5 + 6 = 12
x = 4, y = 16 – 20 + 6 = 2

(1, 2), (0, 6), (-1, 12)
P(x) = (x² + 5x + 6) (x² – 5x + 16)
= x⁴ – 5x³ + 16x² – 5x³ + 25x² – 80x + 6x² – 30x + 96 = 0
= x⁴ – 10x³ + 47x² – 110x + 96 = 0
It has two sign changes
∴ It has two positive real roots
P(-x) = x⁴ + 10x³ + 47x² + 110x + 96
It has no sign change, no negative real roots
y = x² – 5x + 16

Question 3.
Show that the equation x⁹ – 5x⁵ + 4x⁴ + 2x² + 1 = 0 has atleast 6 imaginary solutions.
Solution:P(x) = x⁹ – 5x⁵ + 4x⁴ + 2x² + 1
(i) The number of sign changes in P(x) is 2. The number of positive roots is atmost 2.
(ii) P(-x) = -x⁹ + 5x⁵ + 4x⁴ + 2x² + 1. The number of sign changes in P(-x) is 1. The number of negative roots of P (x) is atmost 1. Since the difference of number of sign changes in P(-x) and number of negative zeros is even.
P(x) has one negative root.
(iii) 0 is not the zero of the polynomial P(x). So the number of real roots is almost 3.
∴ The number of imaginary roots at least 6.

Question 4.
Determine the number of positive and negative roots of the equation x⁹ – 5x⁸ – 14x⁷ = 0.
Solution:
P(x) = x⁹ – 5x⁸ – 14x⁷. It has only one sign change.
∴ It has one positive roots.
P(-x) = -x⁹ – 5x⁸ + 14x⁷. It has only one sign change.
It has one negative root.
∴ It has one positive and one negative roots.

Question 5.
Find the exact number of real roots and imaginary of the equation x⁹ + 9x⁷ + 7x⁵ + 5x³ + 3x.
Solution:
P(x) = x⁹ + 9x⁷ + 7x⁵ + 5x³ + 3x.
There is no change in the sign of P(x) and P(-x), P(x) has no positive and no negative real roots, but 0 is the root of the polynomial equation P(x).

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.4

Question 1.
Solve:
(i) (x – 5) (x – 7) (x + 6)(x + 4) = 504
Solution:
(x – 5) (x + 4) (x – 7) (x + 6) = 504
(x² – x – 20) (x² – x – 42) = 504
Let y = (x² – x)
(y – 20) (y – 42) = 504
⇒ y² – 42y – 20y + 840 = 504
⇒ y² – 62y + 336 = 0
⇒ (y – 56) (y – 6) = 0
⇒ (y – 56) = 0 or (y – 6) = 0
⇒ x² – x – 56 = 0 or x² – x – 6 = 0
⇒ (x – 8) (x + 7) = 0 or (x – 3) (x + 2) = 0
⇒ x = 8, -7 or x = 3, -2
The roots are 8, -7, 3, -2

(ii) (x – 4)(x – 2)(x- 7)(x + 1) = 16
Solution:
(x – 4) (x – 7) (x – 2) (x + 1) = 16
⇒ (x – 4) (x – 2) (x – 7) (x + 1) = 16
⇒ (x² – 6x + 8) (x² – 6x – 7) = 16
Let x² – 6x = y
(y + 8)(y – 7) = 16
⇒ y² – 7y + 8y – 56 – 16 = 0
⇒ y² + y – 72 = 0
⇒ (y + 9) (y – 8) = 0
y + 9 = 0
x² – 6x + 9 = 0
(x – 3)² = 0
x = 3, 3
or
y – 8 = 0
x² – 6x – 8 = 0

Question 2.
Solve:
(2x – 1)(x + 3)(x – 2)(2x + 3) + 20 = 0
Solution:
(x + 3)(x – 2) (2x – 1)(2x + 3) + 20 = 0
(x² + x – 6) (4x² + 6x – 2x – 3) + 20 = 0
(x² + x – 6) (4x² + 4x – 3) + 20 = 0
(x² + x – 6) (x² + 4x – \(\frac{3}{4}\)) + 20 = 0
(÷4) (x² + x – 6) (x² + x – \(\frac{3}{4}\)) + \(\frac{20}{4}\) = 0
Put y = x² + x

4y² – 27y – 38 = 0
4y² – 8y – 19y + 38 = 0
(4y – 19) (y – 2) = 0
y = 2 (or) y = \(\frac{19}{4}\)
x² + x = 2 (or) x² + x = \(\frac{19}{4}\)
x² + x – 2 = 0 (or) 4x² + 4x = 19
(x + 2)(x – 1) = 0 (or) 4x² + 4x – 19 = 0
x = -2 or x = 1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3

Question 1.
Solve the cubic equation: 2x³ – x² – 18x + 9 = 0 if sum of two of its roots vanishes.
Solution:
The given equation is 2x³ – x² – 18x + 9 = 0
\(x^{3}-\frac{x^{2}}{2}-9 x+\frac{9}{2}=0\)
Let the roots be α, -α, β
α – α + β = \(-\left(\frac{-1}{2}\right)\)
\(\Rightarrow \beta=\frac{1}{2}\)
(α) (-α) (β) = \(\frac{-9}{2}\)
\(\Rightarrow-\alpha^{2}\left(\frac{1}{2}\right)=\frac{-9}{2}\)
α² = 9
α = ±3
The roots are 3, -3, \(\frac { 1 }{ 2 }\)

Question 2.
Solve the equation 9x³ – 36x² + 44x – 16 = 0 if the roots form an arithmetic progression.
Solution:
Given the roots are in AP
Let the roots be a – d, a, a + d

Question 3.
Solve the equation 3x³ – 26x² + 52x – 24 = 0 if its roots form a geometric progression.
Solution:

3 + 3λ + 3λ² = 13λ
3λ² + 3λ – 13λ + 3 = 0
3λ² – 10λ + 3 = 0
(λ – 3) (3λ – 1) = 0
λ = 6 or λ = \(\frac{1}{3}\)

Question 4.
Determine k and solve the equation 2x³ – 6x² + 3x + k = 0 if one of its roots is twice the sum of the other two roots.
Solution:
Given cubic equation
2x³ – 6x² + 3x + k = 0
Let the roots be α, β, γ
Given α = 2(β + γ)
β + γ = \(\frac{α}{2}\) ………. (1)
Sum of roots α(β + γ) = 3
From (1) α + \(\frac{α}{2}\) = 3
\(\frac{3α}{2}\) = 3 ⇒ α = 2
Again αβ + βγ + γα = \(\frac{3}{2}\)
α = 2 ⇒ 2β + βγ + 2γ = \(\frac{3}{2}\)
from (1) 2(\(\frac{α}{2}\)) + βγ = \(\frac{3}{2}\)
βγ = \(\frac{3}{2}\) – 2 = \(\frac{3-4}{2}\) = \(\frac{-1}{2}\)
βγ = \(\frac{-1}{2}\) ………… (2)
product of roots α β γ = –\(\frac{k}{2}\)
α = 2 ⇒ 2βγ = –\(\frac{k}{2}\)
βγ = –\(\frac{k}{4}\) ………… (3)

Question 5.
Find all zeros of the polynomial x⁶ – 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135, if it is known that 1 + 2i and √3 are two of its zeros.
Solution:
(i) Given that 1 + 2i, √3
Another roots be 1 – 2i, -√3
sum of roots = 1 + 2i + 1 – 2i
product roots = (1 + 2i)(1 – 2i)
1² + 2² = 1 + 4 = 5
x² – 2x + 5 = 0

(ii) sum of roots = √3 – √3
product roots = (√3)(-√3)
x² – 0x – 3 = 0
x² – 3 = 0
(x² – 2x + 5)(x² – 3) = x⁴ – 2x³ + 2x² + 6x – 15
x⁶– 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135
= (x⁴ – 2x³ + 2x² + 6x – 15)  (x² + px – 9)
Equate of co-efficient of x on both sides
-39 = -54 – 15 p
-39 + 54 = -15 p
15 = -15 p
p = -1
∴ x² – x – 9 = 0

Question 6.
Solve the cubic equations:
(i) 2x³ – 9x² + 10x = 3,
2x³ – 9x² + 10x – 3 = 0
Solution:
(i) 2x³ – 9x² + 10x = 3
2x³ – 9x² + 10x – 3 = 0
sum of the coefficients 2 – 9 + 10 – 3 = 0
∴ x = 1 is one of the roots.

2x² – 7x + 3 = 0
(x – 3)(2x – 1) = 0
x = 3 or x = \(\frac{1}{2}\)
roots are 3, \(\frac{1}{2}\), 1

(ii) 8x³ – 2x² – 7x + 3 = 0
sum of the alternative coefficients are equal
8 – 7 = -2 + 3
1 = 1
∴ (x + 1) is a factor.

8x² – 10x + 3 = 0
(4x – 3) (2x – 1) = 0
4x  = 3 (or) 2x = 1
x = \(\frac{3}{4}\) (or) \(\frac{1}{2}\)
∴ The roots are \(\frac{3}{4}\), \(\frac{1}{2}\), -1

Question 7.
Solve the equation:
x⁴ – 14x² + 45 = 0
Solution:
Put t = x² ⇒ (x²)² – 14x² + 45 = 0
t² – 14t + 45 = 0
t² – 9t – 5t + 45 = 0
t(t – 9) – 5(t – 9) = 0
(t – 9)(t – 5) = 0
t – 9 = 0 or t – 5 = 0
t = 9 or t = 5
x² = 9 or x² = 5
x = ± 3 or y = ±√5
The roots are ±3, ±√5

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2

Question 1.
If k is real, discuss the nature of the roots of the polynomial equation 2x² + kx + k = 0, in terms of k.
Solution:
The given quadratic equation is 2x² + kx + k = 0
a = 2, b = k, c = k
∆ = b² – 4ac = k² – 4(2) k = k² – 8k
(i) If the roots are equal
k² – 8k = 0
⇒ k(k – 8) = 0
⇒ k = 0, k = 8
(ii) If the roots are real
k² – 8k > 0
k(k – 8) > 0
k ∈ (-∞, 0) ∪ (8, ∞)
(iii) If this roots are imaginary
k² – 8k < 0
⇒ k ∈ (0, 8)

Question 2.
Find a polynomial equation of minimum degree with rational coefficients, having 2 + √3 i as a root.
Solution:
Let the root be 2 + i √3
Another root be 2 – i √3
Sum of the roots = 2 + i √3 + 2 – i √3 = 4
Product of the roots = (2 + i √3) (2 – i √3) = 2² + √3² = 4 + 3 = 7
x² – (SR)x + PR = 0
x² – 4x + 7 = 0

Question 3.
Find a polynomial equation of minimum degree with rational coefficients, having 2i + 3 as a root.
Solution:
Given roots is (3 + 2i), the other root is (3 – 2i);
Since imaginary roots occur in with real co-efficient occurring conjugate pairs.
x² – x(S.O.R) + P.O.R = 0
⇒ x² – x(6) + (9 + 4) = 0
⇒ x² – 6x + 13 = 0

Question 4.
Find a polynomial equation of minimum degree with rational coefficients, having √5 – √3 as a root.
Solution:
Let the root be √5 – √3,
Another root is √5 + √3
Sum of the roots = √5 – √3 + √5 + √3 = 2√5
Product of roots = (√5 – √3) (√5 + √3)
√5² – √3² = 5 – 3 = 2
x² – (SR)x + PR = 0
x² – 2√5 x + 2 = 0 which is not rational co-efficient.
to make rational co-efficient
(x² + 2√5 x + 2) (x² + 2 + 2√5 x) = 0
(x² + 2)² – (2√5x)² = 0
x⁴ + 4 + 4x² – 20x² = 0
⇒ x⁴ – 16x² + 4 = 0 is a rational co-efficient polynomial equation.

Question 5.
Prove that a straight line and parabola cannot intersect at more than two points.
Solution:
Let the standard equation of parabola y² = 4ax …..(1)
Equation of line be y = mx + c …(2)
Solving (1) & (2)
(mx + c)² = 4ax
⇒ mx² + 2mcx + c² – 4ax = 0
⇒ mx² + 2x(mc – 2a) + c² = 0
This equation can not have more than two solutions and
hence a line and parabola cannot intersect at more than two points.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.1

Question 1.
If the sides of a cubic box are increased by 1, 2, 3 units respectively to form a cuboid, then the volume is increased by 52 cubic units. Find the volume of the cuboid.
Solution:
Let the side of the cube be ‘x’
Sides of cuboid are (x + 1) (x + 2) (x + 3)
∴ Volume of cuboid = x³ + 52
⇒ (x + 1) (x + 2) (x + 3) = x³ + 52
⇒ (x² + 3x + 2)(x + 3) = x³ + 52
⇒ x³ + 3x² + 3x² + 9x + 2x + 6 – x³ – 52 = 0
⇒ 6x² + 11x – 46 = 0 (÷2)
⇒ (x – 2) (6x + 23) = 0
⇒ x – 2 = 0 or 6x + 23 = 0
⇒ x = 2 or x = \(-\frac{23}{6}\) (not possible)
∴ x = 2
Volume of cube = 2³ = 8
Volume of cuboid = 52 + 8 = 60 cubic units

Question 2.
Construct a cubic equation with roots
Solution:
(i) 1, 2, and 3
α = 1, β = 2, γ = 3
α + β + γ = 6
αβ + βγ + γα = 2 + 6 + 3 = 11
αβγ = 6
x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ = 0
x³ – 6x² + 11x – 6 = 0

(ii) 1, 1, and -2
α = 1, β = 1, γ = -2
α + β + γ = 1 + 1 – 2 = 0
αβ + βγ + γα = 1 – 2 – 2 = -3
αβγ = 1(1)(-2) = -2
x³ – 0x² – 3x + 2 = 0
∴ x³ – 3x + 2 = 0

(iii) 2, \(\frac { 1 }{ 2 }\), and 1.

Multiplying by 2
2x³ – 7x² + 7x – 2 = 0

Question 3.
If α, β and γ are the roots of the cubic equation x³ + 2x² + 3x + 4 = 0, form a cubic equation whose roots are
(i) 2α, 2β, 2γ,
(ii) \(\frac{1}{α}\), \(\frac{1}{β}\), \(\frac{1}{γ}\)
(iii) – α, – β, – γ
Solution:
(i) Given that α, β, γ are the roots of x³ + 2x² + 3x + 4 = 0
Compare with x³ + bx² + cx + d = 0
b = 2, c = 3, d = 4
α + β + γ = -6 = -2
αβ + βγ + γα = c = 3
αβγ = -d = -4
Given roots are 2α, 2β, 2γ
2α + 2β + 2γ = 2 (α + β + γ)
= 2 (-2)
= -4
(2α) (2β) + (2β) (2γ) + (2γ) (2α) = (4αβ + 4βγ + 4γα)
= 4(αβ + βγ + γα)
= 4(3)
= 12
(2α) (2β) (2γ) = 8(αβγ)
= 8(-4)
= -32
The equation is
x³ – x² (2α + 2β + 2γ) + x (4αβ + 4βγ + 4γα) – 8 (αβγ) = 0
⇒ x³ – x² (-4) + x (12) – (-32) = 0
⇒ x³ + 4x² + 12x + 32 = 0

(ii) The new roots are \(\frac{1}{α}\), \(\frac{1}{β}\), \(\frac{1}{γ}\)

⇒ 4x³ + 3x² + 2x + 1 = 0

(iii) The given roots are -α, -β, -γ
The cubic equation is
x³ – x² (-α – β – γ) + x (αβ + βγ + γα) + (αβγ) = 0
⇒ x³ + x² (α + β + γ) + x (αβ + βγ + γα) + (αβγ) = 0
⇒ x³ + x² (-2) + x (3) – 4 = 0
⇒ x³ – 2x² + 3x – 4 = 0

Question 4.
Solve the equation 3x³ – 16x² + 23x – 6 = 0 if the product of two roots is 1.
Solution:
Let the roots be α, β, γ
Given αβ = 1, β = \(\frac{1}{α}\)

⇒ 3α² – 10α + 3 = 0
3α² – 9α – α + 3 = 0
3α(α – 3) -1(α – 3) = 0
(3α – 1) (α – 3) = 0
α = 3 or α = \(\frac{1}{3}\)
If α = 3, β = \(\frac{1}{3}\), γ = 2 (or)
α = \(\frac{1}{3}\), β = 3, γ = 2
⇒ [α, β, γ] = (\(\frac{1}{3}\), 3, 2)

Question 5.
Find the sum of squares of roots of the equation 2x⁴ – 8x³ + 6x² – 3 = 0.
Solution:
The given equation is 2x⁴ – 8x³ + 6x² – 3 = 0.
(÷ 2) ⇒ x⁴ – 4x³ + 3x² – \(\frac{3}{2}\) = 0
Let the roots be α, β, γ, δ
α + β + γ + δ = -b = 4
(αβ + βγ + γδ + αδ + αγ + βδ) = c = 3
αβγ + βγδ + γδα = -d = 0
αβγδ = \(\frac{-3}{2}\)
To Find α² + β² + γ² + δ² = (α + β + γ + δ)² – 2 (αβ + βγ + γδ + αδ + αγ + βδ)
= (4)² – 2(3)
= 16 – 6
= 10

Question 6.
Solve the equation x³ – 9x² + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3 : 2.
Solution:
Let the roots are 3α, 2α, β
sum of the roots are
3α + 2α + β = 9
5α + β = 9 ………. (1)
Product of two roots
3α(2α) + 2α(β) + β(3α) = 14
6α² + 5αβ = 14 ……… (2)
Product of three roots
(3α) (2α)β = -24
α²β = -4 ………. (3)
(1) ⇒ β = 9 – 5 α
(2) ⇒ 6α² + 5α (9 – 5α) = 14
6α² + 45α – 25α² = 14
-19α² + 45α – 14 = 0
19α² – 45α + 14 = 0
(α – 2) (α – \(\frac{7}{19}\)) = 0
α = 2 or α = \(\frac{7}{19}\)
If α = 2, β = 9 – 5 (α) = 9 – 5(2) = 9 – 10 = -1
roots are 3α, 2α, β
3(2), 2(2), -1 (i,e.,) 6, 4, -1
If α = \(\frac{7}{19}\), β = 9 – 5(\(\frac{7}{19}\)) = (\(\frac{136}{19}\))
roots are 3α, 2α, β (i,e.,) \(\frac{21}{19}\), \(\frac{14}{19}\), \(\frac{136}{19}\)

Question 7.
If α, β, and γ are the roots of the polynomial equation ax³ + bx² + cx + d = 0, find the value of Σ\(\frac{α}{βγ}\) terms of the coefficients.
Solution:

Question 8.
If α, β, γ and δ are the roots of the polynomial equation 2x⁴ + 5x³ – 7x² + 8 = 0, find a quadratic equation with integer coefficients whose roots are α + β + γ + δ and αβγδ.
Solution:

pq = (\(\frac{-5}{2}\))(4) = -10
x² – (p + q)x + pq = 0
x² – \(\frac{3}{2}\)x – 10 = 0
2x² – 3x – 20 = 0

Question 9.
If p and q are the roots of the equation lx² + nx + n = 0,
show that,
Solution:
p and q are the roots of the equation lx² + nx + n = 0
p + q = –\(\frac{n}{l}\), pq = \(\frac{n}{l}\)
LHS

Question 10.
If the equations x² + px + q = 0 and x² + p’x + q’ = 0 have a common root, show
that it must be equal to \(\frac{pq’-p’q}{q-q’}\) and \(\frac{q-q’}{p’-p}\)
Solution:
Let it be α common roots of x² + px + q = 0
x² + p’x + q’ = 0
(i,e.,) α² + pα + q = 0 …… (1) and
α² + p’α + q’ = 0 ………. (2)
Solving 1 and 2 by cross multiplication method, we have

Hence proved.

Question 11.
A 12-meter tall tree was broken into two parts. It was found that the height of the part which was left standing was the cube root of the length of the part that was cut away. Formulate this into a mathematical problem to find the height of the part which was cut away.
Solution:
Let the height of the tree = 12
length of the cut part = x³
Length of left out part = \(\sqrt[3]{x^{3}}\)
= x
Given x + x³ = 12
x³ + x – 12 = 0

Which is required mathematical problem

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.9 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.9

Choose the most suitable answer.

Question 1.
iⁿ + iⁿ⁺¹+ iⁿ⁺² + iⁿ⁺³ is:
(a) 0
(b) 1
(c) -1
(d) z
Solution:
(a) 0
Hint:
iⁿ + iⁿ⁺¹+ iⁿ⁺² + iⁿ⁺³
= iⁿ[1 + i + i² + i³]
= iⁿ[1 + i – 1 – i]
iⁿ (0) = 0

Question 2.
The value of \(\sum _{ i=1 }^{ 13 }{ ({ i }^{ n }+{ i }^{ n-1 }) } \) is
(a) 1 + i
(b) i
(c) 1
(d) 0
Solution:
(a) 1 + i
Hint:
\(\sum _{ i=1 }^{ 13 }{ ({ i }^{ n }+{ i }^{ n-1 }) } \)= (i¹ + i² + i³ + … + i¹³) + (i⁰ + i¹ + i² + … + i¹²)
= i⁰ + 2(i¹ + i² + i³  + ….. i¹²) + i¹³
= 1 + 2(i – 1 – i + 1 + … + 1) + 1
= 1 + 2(0) + i = 1 + i

Question 3.
The area of the triangle formed by the complex numbers z, iz, and z + iz in the Argand’s diagram is:
(a) \(\frac{1}{2}\) |z|²
(b) |z|²
(c) \(\frac{3}{2}\) |z|²
(d) 2|z|²
Solution:
(a) \(\frac{1}{2}\) |z|²
Hint:
Area of the triangle formed by the complex numbers z, iz and z + iz.
Let z = a + ib ⇒point (a, b)
iz = – b + ia ⇒ point (- b, a)
z + iz =(a – b) + i(a + b) point((a – b),(a + b))
Area of the triangle
= \(\frac {1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac {1}{2}\) [a(a – a – b) -b(a + b – b) + (a – b)(b – a)]
= \(\frac {1}{2}\) [-ab – ab + ab – a² – b² + ab]

Question 4.
The conjugate of a complex number is \(\frac{1}{i-2}\) Then, the complex number is:
(a) \(\frac{1}{i+2}\)
(b) \(\frac{-1}{i+2}\)
(c) \(\frac{-1}{i-2}\)
(d) \(\frac{1}{i-2}\)
Solution:
(b) \(\frac{-1}{i+2}\)
Hint:
Conjugate of complex number is \(\frac{1}{i-2}\)
∴ the complex number is \(\frac{-1}{i+2}\)

Question 5.
If z = \(\frac{(√3+i)^3(3i+4)²}{(8+6i)²}\)
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(c) 2
Hint:

Question 6.
If z is a non zero complex number, such that 2iz² = \(\bar { z }\) then | z | is:
(a) \(\frac{1}{2}\)
(b) 0
(c) 1
(d) 2
Solution:
z is a non zero complex number
Given 2iz² = \(\bar { z }\)
let z = x + iy
2i(x + iy)² = x – iy
simplifying 2i(x² – y² + 2ixy) = x – iy
-4xy + 2i(x² – y²) = x – iy
Equating real and imaginary parts
-4xy = x, 2(x² – y²) = -y
solving x = \(\frac{√3}{4}\), y =-\(\frac{1}{4}\)
z = \(\frac{√3}{4}\) – \(\frac{i}{4}\)
|z| = \(\sqrt { \frac{3}{16}+\frac{1}{16}}\) = \(\sqrt { \frac{1}{4}}\)
= \(\frac {1}{2}\)

Question 7.
If |z – 2 + i | ≤ 2, then the greatest value of |z| is:
(a) √3 – 2
(b) √3 + 2
(c) √5 – 2
(d) √5 + 2
Solution:
(d) √5 + 2
Hint:
|z – 2 + i | ≤ 2
|z + (-2 + i)| ≤ |z| + |-2 + i|
|z| ± √5
Given |z – 2 + i| ≤ 2
∴ |z| ± √5 ≤ 2
|z| ≤ 2 – √5. |z| ≤ 2 + √5
∴ The greatest value is 2 + √5

Question 8.
If |z – \(\frac{3}{2}\)| = 2 then the least value of |z| is:
(a) 1
(b) 2
(c) 3
(d) 5
Solution:
(a) 1
Hint:

|z|² – 2 |z| + 1 ≤ 3 + 1
(|z| – 1)² ≤ 4
|z| – 1 ≤ ± 2
|z| ≤ 2 + 1 and |z| ≤ – 2 + 1
|z| = -1
But |z| = 1

Question 9.
If |z| = 1, then the value of \( \frac { 1+z }{ 1+\bar { z } } \) is
(a) z
(b) \( \bar { z } \)
(c) \(\frac{1}{z}\)
(d) 1
Solution:
(a) z
Hint:

Question 10.
The solution of the equation |z| – z = 1 + 2i is:
(a) \(\frac{3}{2}\) – 2i
(b) – \(\frac{3}{2}\) + 2i
(c) 2 – \(\frac{3}{2}\)i
(d) 2 + \(\frac{3}{2}\)i
Solution:
(a) \(\frac{3}{2}\) – 2i
Hint:
|z| – z = 1 + 2i
Let z = x + iy
|z| = x + iy + 1 + 2i
\(\sqrt{x^2+y^2}\) = (x + 1) + i(y + 2)
\(\sqrt{x^2+y^2}\) = x + 1 y + 2 = 0
x² + y² = (x + 1)² y = -2
y² = 2x + 1
2x = 3
x = \(\frac{3}{2}\)
∴z = x + iy = \(\frac{3}{2}\) – 2i

Question 11.
If |z₁| = 1,|z₂| = 2, |z₃| = 3 and |9z₁z₂ + 4z₁z₃ + z₂z₃| = 12, then the value of |z₁ + z₂ + z₃| is:
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2
Hint:

Question 12.
If z is a complex number such that z∈C\R and z + \(\frac{1}{z}\) ∈R, then |z| is:
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:
If z ∈ C\R and z + \(\frac{1}{z}\) ∈ R
Then |z| = 1

Question 13.
z₁, z₂ and z₃ are complex numbers such that z₁ + z₂ + z₃ = 0 and |z₁| = |z₂| = |z₃| = 1 then \({ z }_{ 1 }^{ 2 }+{ z }_{ 2 }^{ 2 }+{ z }_{ 3 }^{ 2 }\) is
(a) 3
(b) 2
(c) 1
(d) 0
Solution:
(d) 0

Question 14.
If \(\frac{z-1}{z+1}\)is purely imaginary, then |z| is
(a) \(\frac{1}{2}\)
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:

Question 15.
If z = x + iy is a complex number such that |z + 2| = |z – 2|, then the locus of z is:
(a) real axis
(b) imaginary axis
(c) ellipse
(d) circle
Solution:
(b) imaginary axis
Hint:
|z + 2| = |z – 2|
Let z = x + iy
|(x + 2) + iy| = |(x – 2) + iy|
(x + 2)² + y² = (x – 2)² + y²
x² + 4x + 4 = x² – 4x + 4
⇒ x = 0

Question 16.
The principal argument of \(\frac{3}{-1+i}\) is:
(a) \(\frac{-5π}{6}\)
(b) \(\frac{-2π}{3}\)
(c) \(\frac{-3π}{4}\)
(d) \(\frac{-π}{2}\)
Solution:
(c) \(\frac{-3π}{4}\)
Hint:

Since Real and imaginary parts are negative.
‘θ’ lies in 3rd quadrant.
∴ Principal argument = – \(\frac {3π}{4}\) [∵ \(\frac {π}{4}\) – π]

Question 17.
The principal argument of (sin 40° + i cos 40°)⁵ is:
(a) – 110°
(b) -70°
(c) 70°
(d) 110°
Solution:
(a) – 110°
Hint:
z = (sin 40° + i cos 40°)⁵
= (cos 50° + i sin 50°)⁵
= cos 250° + i sin 250°]
= cos (360° – 110°) + i sin (360° – 110°)
= cos 110° – i sin 110°
= cos (-110°) + i sin (-110°)
∴ Principal argument is – 110°

Question 18.
If (1 + i) (1 + 2i) (1 + 3i) ……. (l + ni) = x + iy, then 2.5.10 …… (1 + n²) is:
(a) 1
(b) i
(c) x² + y²
(d) 1 + n²
Solution:
(c) x² + y²
Hint:
(1 + i) (i + 2i) ….. (1 + ni) = x + iy
Taking of two modulli of each of squaring
2.5.10 … (1 +n²) = x²+ y²

Question 19.
If ω ≠ 1 is a cubic root of unity and (1 + ω)⁷ = A + Bω, then (A, B) equals:
(a) (1, 0)
(b) (-1, 1)
(c) (0, 1)
(d) (1, 1)
Solution:
(d) (1, 1)
Hint:
(1 + ω)⁷ = A + Bω
(- ω²)⁷ = A + Bω
– ω¹⁴ = A + Bω
– ω² = A + Bω
1 + ω² = A + Bω
∴ A = 1, B = 1

Question 20.
The principal argument of the complex number \(\frac{(1+i \sqrt{3})^{2}}{4 i(1-i \sqrt{3})}\) is:
(a) \(\frac{2π}{3}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{5π}{6}\)
(d) \(\frac{π}{2}\)
Solution:
(d) \(\frac{π}{2}\)
Hint:

Question 21.
If α and β are the roots of x² + x + 1 = 0, then α²⁰²⁰ + β²⁰²⁰ is
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
(b) -1
Hint:
x² + x + 1 = 0

Question 22.
The product of all four values of (cos\(\frac{π}{3}\) + i sin \(\frac{π}{3}\))^{\(\frac{3}{4}\)} is:
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
(c) 1

Question 23.
If ω ≠ 1 is a cubic root of unity and

(a) 1
(b) -1
(c) √3 i
(d) -√3 i
Solution:
(d) -√3 i

= 1(ω² – ω⁴) – (ω – ω²) + 1(ω² – ω) = 3k
= ω² – ω – ω + ω² + ω² – ω = 3k
= 3ω² – 3ω = 3k
= 3(ω² – ω) = 3k
∴ k = ω² – ω

Question 24.
The value of (\(\frac{1+√3 i}{1-√3 i}\))¹⁰ is:
(a) cis\(\frac{2π}{3}\)
(b) cis\(\frac{4π}{3}\)
(c) -cis\(\frac{2π}{3}\)
(d) -cis\(\frac{2π}{3}\)
Solution:
(a) cis\(\frac{2π}{3}\)
Hint:

Question 25.
If ω = cis\(\frac{2π}{3}\), then the number of distinct roots of
(a) 1
(b) 2
(c) 3
(d) 4
Solution:


The expansion 1 becomes
z³ + (0) z² + (0) z + 0 = 0
⇒ z³ = 0
z = 0 is the only solution.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.8 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.8

Question 1.
If to ω ≠ 1 is a cube root of unity, then show that

Solution:
L.H.S

Question 2.
Show that

Solution:

Question 3.

Solution:


Aliter method:

Question 4.
If 2cos α = x + \(\frac{1}{x}\) and 2 cos β = y + \(\frac{1}{x}\), show that
(i) \(\frac{x}{y}+\frac{y}{x}=2 \cos (\alpha-\beta)\)
Solution:
Given 2 cos α = x + \(\frac{1}{x}\) and cos β = y + \(\frac{1}{y}\)
simplifying x² – 2x cos α + 1 = 0

if x = cos α + i sin α, then \(\frac{1}{x}\) = cos α – i sin α
similarly y = cos β + i sin β and \(\frac{1}{y}\) = cos β – i sin β

Hence proved

(ii) xy = (cos α + i sin α)(cos β + i sin β )
Solution:
xy = (cos α + i sin α) (cos β + i sin β)
= cos (α + β) + i sin (α + β)
[∵ arg (z₁z₂) = arg z₁ + arg z₂
\(\frac{1}{xy}\) = cos (α + β) – i sin (α + β)
∴ xy – \(\frac{1}{xy}\) = cos (α + β) + i sin (α + β) – cos (α + β) + i sin (α + β)
= 2i sin (α + β)
Hence proved

(iii) \(\frac{x^{m}}{y^{n}}-\frac{y^{n}}{x^{m}}\) = 2 i sin (mα – nβ)
Solution:

Hence Proved

(iv) x^m yⁿ + \(\frac { 1 }{ x^m y^n }\) = 2 cos(mα – nβ)
Solution:
= (cos mα + sin mα) (cos nβ + i sin nβ)
= cos (mα + nβ) + i sin (mα + nβ)

Hence proved

Question 5.
Solve the equation z³ + 27 = 0.
Solution:
z³ + 27 = 0
z³ = – 27 = 27 (-1)
= 27 [cos(π + 2kπ) + i sin(π + 2kπ)], k ∈ z
∴ z = (27)^1/3[cos (2k + 1)π + i sin (2k+1)π]^1/3 k ∈ z

Question 6.
If ω ≠ 1 is a cube root of unity, show that the roots of the equation (z – 1)³ + 8 = 0 are -1, 1 – 2ω, 1 – 2ω².
Solution:
Given ω ≠ 1 is a active root of unity
(z – 1)³ + 8 = 0
(z- 1)³ = -8
z – 1 = (-8)^1/3 (1)^1/3
= (-2) (1, ω, ω²)
z – 1 = (-2, -2ω, -2ω²)
= z – 1 = -2
z = -2 + 1 = -1
z – 1 = -2ω
z = 1 – 2ω
z – 1 = -2ω²
z = 1 – 2ω²

Question 7.

Solution:
\(\sum_{k=1}^{8}\) (cos \(\frac { 2kπ }{ 9 }\) + i sin \(\frac { 2kπ }{ 9 }\))
The sum all nth root of unity is
1 + ω + ω² + …….. + ω^n-1 = 0
From the given polar from , it is clear that the complex number is 1 + i0 (unity)

Question 8.
If ω ≠ 1 is a cube root of unity, show that
(i) (1 – ω + ω²)⁶ + (1 + ω – ω²)⁶ = 128.
Solution:
ω is a cube root of unity ω³ = 1; 1 + ω + ω² = 0
(1 – ω + ω²)⁶ + (1 + ω – ω²)⁶
= (-ω – ω)⁶ + (-ω² – ω²)⁶
= (-2ω)⁶ + (-2ω²)⁶
= (-2)⁶(ω⁶ + ω¹²)
= (64)(1 + 1)
= 128

(ii) (1 + ω) (1 + ω²) (1 + ω⁴) (1 + ω⁸)….. (1 + ω²ⁿ) = 1
Solution:
(1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸) …… (1 + ω²ⁿ)
= (1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸) ……. 2n factors
= (-ω²)(-ω)(-ω²)(-ω) …… 2n factors
= ω³. ω³
= 1
Hence proved.

Question 9.
If z = 2 – 2i, find the rotation of z by θ radians in the counterclockwise direction about the origin when
Solution:
Let 2 – 2i
Modules = |z| = \(\sqrt{2^2+2^2}\) = 2√2
Argument θ = tan^-1(\(\frac{-2}{2}\)) = tan^-1(-1) = –\(\frac{π}{4}\)
(i) when ‘z’ is rotated in the counter clockwise direction about the origin when θ = \(\frac{π}{3}\) i.,e argument of new position

(ii) θ = \(\frac{2π}{3}\)
Solution:

(iii) θ = \(\frac{3π}{3}\)
Solution:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.7 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7

Question 1.
Write in polar form of the following complex numbers.
(i) 2 + i2 √3
Solution:
Let z + i2√3 = r (cos θ + i sin θ)
equating real and imaginary parts
r cos θ = 2 (+ve)
r sin θ = 2√3 (+ve)
r² cos² θ + r² sin² θ = (2)² + (2√3)²
r² = 4 + 12 = 16
|z| = r = 4
since cos cos θ and sin θ are positive ‘θ’ lies in 1st quadrant.
cos θ = \(\frac{1}{2}\), sin θ = \(\frac{√3}{2}\)
∴ θ = sin θ = \(\frac{π}{3}\) (or) θ = tan^-1 |\(\frac{y}{x}\)|
= tan^-1 |\(\frac{2√3}{2}\)|
= tan^-1 √3 = \(\frac{π}{3}\)
∴ argument = 2kπ + \(\frac{π}{3}\)
∴ Polar form is z = r (cos θ + i sin θ)
2 + 2i√3 = 4 (cos (2kπ + \(\frac{π}{3}\)) + i sin(2kπ +\(\frac{π}{3}\))) k ∈ z

(ii) 3 – i √3
Solution:
Let z = 3 – i √3 = r (cos θ + i sin θ)
equating real and imaginary parts
r cos θ = 3 (+ve)
r sin θ = -√3 (-ve)
r² cos² θ + r² sin² θ = (3)² + (-√3)²
r² = 9 + 3 = 12
|z| = r = 2√3
since cos cos θ positive and sin θ in -ve so lies in IV quadrant.
cos θ = \(\frac{√3}{2}\), sin θ = \(\frac{-1}{2}\), θ = \(\frac{-π}{6}\)
argument = 2kπ – \(\frac{π}{6}\), k ∈ Z
polar from z = r(cos θ + i sin θ)
3 – i√3 = 2√3 (cos (2kπ – \(\frac{π}{6}\)) + i sin(2kπ – \(\frac{π}{6}\))) k ∈ Z

(iii) -2 – i 2 = r (cos θ + i sin θ)
Solution:
Let z = -2 – i2 = r(cos θ + i sin θ)
equating real and imaginary parts
r cos θ = -2
r sin θ = -2
r² cos² θ + r² sin² θ = (-2)² + (-2)²
r² = 4 + 4 = 8
r² = 8
|z| = r = 2√2
cos θ = \(\frac{-2}{2√2}\) = \(\frac{-1}{√2}\), sin θ = \(\frac{-2}{2√2}\) = \(\frac{-1}{√2}\)
since cos θ and sin θ both are in -ve so lies in III quadrant.
argument = 2kπ – 3\(\frac{π}{4}\)
as θ = \(\frac{π}{4}\) – π = –\(\frac{3π}{4}\)
polar from z = r(cos θ + i sin θ)
-2 – i2 = 2√2 (cos (2kπ – \(\frac{3π}{4}\)) + i sin(2kπ – \(\frac{3}{4}\))) k ∈ Z

(iv) \(\frac{i-1}{cos{\frac{π}{3}}+isin{\frac{π}{3}}}\)
Solution:

Question 2.
Find the rectangular form of the complex numbers

Solution:

Solution:

Question 3.
\(\left(x_{1}+i y_{1}\right)\left(x_{2}+i y_{2}\right)\left(x_{3}+i y_{3}\right) \cdots\left(x_{n}+i y_{n}\right)=a+i b\), show that

Solution:
Let (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n) = a + ib
Taking modulus
|(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n)| = |a + ib|
|x₁ + iy₁| |x₂ + iy₂| |x₃ + iy₃| …… |x_n + iy_n| = |a + ib|
\(\sqrt{x_{1}^{2}+y_{1}^{2}} \sqrt{x_{2}^{2}+y_{2}^{2}} \sqrt{x_{3}^{2}+y_{3}^{2}} \ldots \sqrt{x_{n}^{2}+y_{n}^{2}}\) = \(\sqrt{a^2+b^2}\)
Squaring on both sides
\(\left(x_{1}^{2}+y_{1}^{2}\right)\left(x_{2}^{2}+y_{2}^{2}\right)\left(x_{3}^{2}+y_{3}^{2}\right) \ldots\left(x_{n}^{2}+y_{n}^{2}\right)\) = a² + b²
Hence proved

(ii) \(\sum_{r=1}^{n}\) tan^-1 (\(\frac{y_r}{x_r}\)) = tan^-1 (\(\frac{b}{a}\)) + 2kπ, k ∈ Z
Solution:
Let (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n) = a + ib
Taking arguments
arg [(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n)] = arg (a + ib)
arg (x₁ + iy₁) + arg(x₂ + iy₂) + arg (x₃ + iy₃) …… + arg(x_n + iy_n) = arg(a + ib)

Question 4.
Given \(\frac{1+z}{1-z}\) = cos 2θ + i sin 2θ, show that To prove that z = i tan θ.
Solution:

Squaring on both sides
(1 + x)² + y² = (1 – x)² + y²
1 + 2x + x² + y² = 1 – 2x + x² +y²
x = 0
∴ z = 0 + iy = iy

∴ y = tan θ
hence z = iy
z = i tan θ

Question 5.
If cos α + cos β + cos γ = sin α + sin β + sin γ = 0. then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) and
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ).
Solution:
Let a = cos α + i sin α = e^iα
b = cos β + i sin β = e^iβ
c = cos γ + i sin γ = e^iγ
a + b + c = (cos α + cos β + cos γ) + i (sin α + sin β + sin γ)
⇒ a + b + c = 0 + i 0
⇒ a + b + c = 0
If a + b + c = 0 then a³ + b³ + c³ = 3abc

(cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ) = 3 [cos (α + β + γ) + i sin (α + β + γ)]
(cos 3α + cos 3β + cos 3γ) + i (sin 3α + sin 3β + sin 3γ) = 3 cos (α + β + γ) + i 3sin(α + β + γ)
Equating real and Imaginary parts
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)

Question 6.
If z = x + iy and arg \(\left(\frac{z-i}{z+2}\right)\) = \(\)\frac{π}{4}, then show that x² + y³ + 3x – 3y + 2 = 0.
Solution:

2y – x – 2 = x² + 2x + y² – y
x² + y² + 2x + x – y – 2y + 2 = 0
⇒ x² + y² + 3x – 3y + 2 = 0
Hence proved

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.6

Question 1.
If 2 = x + iy is a complex number such that \(\left|\frac{z-4 i}{z+4 i}\right|\) = 1 show that the locus of z is real axis.
Solution:
Let z = x + iy

Squaring on both sides
x² + (y – 4)² =  x² + (y + 4)²
simplifying
We get y = 0
Which is real axis

Question 2.
If z = x + iy is a complex number such that Im \(\left(\frac{2 z+1}{i z+1}\right)\) = 0, show that the locus of z is 2x² + 2y² + x – 2y = 0.
Solution:
Let z = x + iy

2y(1 – y) – x(2x + 1) = 0
⇒ 2y – 2y² – 2x² – x = 0
∴ The locus is 2x² + 2y² – 2y + x = 0
Hence proved

Question 3.
Obtain the Cartesian form of the locus of z = x + iy in each of the following cases:
(i) [Re (iz)]² = 3
Solution:
z = x + iy
[Re(iz)]² = 3
⇒ [Re[i(x + iy]]² = 3
⇒ [Re(ix – y)]² = 3
⇒ (-y)² = 3
⇒ y² = 3

(ii) Im[(1 – i)z + 1] = 0
⇒ Im [(1 – i)(z + iy) + 1] = 0
⇒ Im[x + iy – ix + y + 1] = 0
⇒ Im[(x + y + 1) + i(y – x)] = 0
Considering only the imaginary part
y – x = 0 ⇒ x = y

(iii) |z + i| = |z – 1|
⇒ |x + iy + i| = | x + iy – 1|
⇒ |x + i(y + 1)| = |(x – 1) + iy|
Squaring on both sides
|x + i(y + 1)|² = |(x – 1) + iy|²
⇒ x² + (y + 1)² = (x – 1)² + y²
⇒ x² + y² + 2y + 1 = x² – 2x + 1 + y²
⇒ 2y + 2x = 0
⇒ x + y = 0

(iv) \(\bar {z}\) = z^-1
Solution:

x² + y² = 1, x² + y² = -1 which cannot be true.
∴ x² + y² = 1

Question 4.
Show that the following equations represent a circle, and, find its centre and radius.
(i) |z – 2 – i| = 3
Solution:
Let z = x + iy
|z – 2 – i| = 3
⇒ |x + iy – 2 – i| = 3
⇒ |(x – 2) + i(y – 1)| = 3
⇒ \(\sqrt{(x-2)^{2}+(y-1)^{2}}=3\)
Squaring on both sides
(x – 2)² + (y – 1)² = 9
⇒ x² – 4x + 4 + y² – 2y + 1 – 9 = 0
⇒ x² + y² – 4x – 2y – 4 = 0 represents a circle
2g = -4 ⇒ g = -2
2f = -2 ⇒ f = -1
c = -4
(a) Centre (-g, -f) = (2, 1) = 2 + i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{4+1+4}=3\)
Aliter: |z – (2 + i)| = 3
Centre = 2 + i
radius = 3

(ii) |2(x + iy) + 2 – 4i| = 2
⇒ |2x + i2y + 2 – 4i| =2
⇒ |(2x + 2) + i(2y – 4)| = 2
⇒ |2(x + 1) + 2i(y – 2)| = 2
⇒ |(x + 1) + i(y – 2)| = 1
⇒ \(\sqrt{(x+1)^{2}(y-2)^{2}}=1\)
Squaring on both sides,
x² + 2x + 1 + y² + 4 – 4y – 1 = 0
⇒ x² + y² + 2x – 4y + 4 = 0 represents a circle
2g = 2 ⇒ g = 1
2f = -4 ⇒ f = -2
c = 4
(a) Centre (-g, -f) = (-1, 2) = -1 + 2i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-4}=1\)
Aliter: 2|(z + 1 – 2i)| = 2
|z – (-1 + 2i)| = 1
Centre = -1 + 2i
radius = 1

(iii) |3(x + iy) – 6 + 12i| = 8
⇒ |3x + i3y – 6 + 12i| = 8
⇒ |3(x – 2) + i3 (y + 4)| = 8
⇒ 3|(x – 2) + i (y + 4)| = 8
⇒ \(3 \sqrt{(x-2)^{2}+(y+4)^{2}}=8\)
Squaring on both sides,
9[(x – 2)² + (y + 4)²] = 64
⇒ x² – 4x + 4 + y² + 8y + 16 = \(\frac{64}{9}\)
⇒ x² + y² – 4x + 8y + 20 – \(\frac{64}{9}\) = 0
x² + y² – 4x + 8y + \(\frac{116}{9}\) = 0 represents a circle.
2g = -4 ⇒ g = -2
2f = 8 ⇒ f = 4
c = \(\frac{116}{9}\)
(a) Centre (-g, -f) = (2, -4) = 2 – 4i
(b) Radius = \(=\sqrt{g^{2}+f^{2}-c}=\sqrt{4+16-\frac{116}{9}}=\sqrt{\frac{180-116}{9}}=\frac{8}{3}\)
Aliter:
|z – 2 + 4i| = \(\frac{8}{3}\)
⇒ |z – (2 – 4i)| = \(\frac{8}{3}\)
Centre = 2 – 4i, Radius = \(\frac{8}{3}\)

Question 5.
Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases:
(i) |z – 4| = 16
Solution:
Let z = x + iy
|x + iy – 4| – 16
|(x – 4) + iy| = 16
\(\sqrt{(x – 4)² + y²}\) = 16
∴ Squaring on both sides
(x – 4)² + y² = 256
x² – 8x + 16 + y² – 256 = 0
x² + y² – 8x – 240 = 0
The locus of the point is a circle.

(ii) |z – 4|² – |z – 1|² = 16.
Solution:
|x + iy – 4|² – |x + iy – 1|² = 16
⇒ |(x – 4) + iy|² – |(x – 1) + iy|² = 16
⇒ [(x – 4)² + y²] – [(x – 1)² + y²] = 16
⇒ (x² – 8x + 16 + y²) – (x² – 2x + 1 + y²) = 16
⇒ x² + y² – 8x + 16 – x² + 2x – 1 – y² = 16
⇒ -6x + 15 = 16
⇒ 6x + 1 = 0
The locus of the point is a straight line.