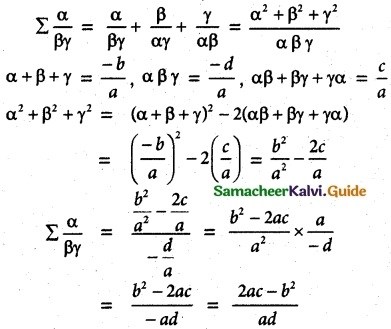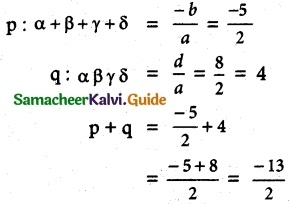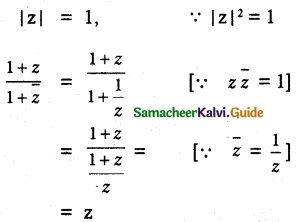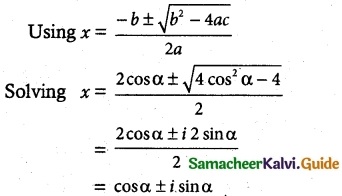Bhagya

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2

Question 1.
If k is real, discuss the nature of the roots of the polynomial equation 2x² + kx + k = 0, in terms of k.
Solution:
The given quadratic equation is 2x² + kx + k = 0
a = 2, b = k, c = k
∆ = b² – 4ac = k² – 4(2) k = k² – 8k
(i) If the roots are equal
k² – 8k = 0
⇒ k(k – 8) = 0
⇒ k = 0, k = 8
(ii) If the roots are real
k² – 8k > 0
k(k – 8) > 0
k ∈ (-∞, 0) ∪ (8, ∞)
(iii) If this roots are imaginary
k² – 8k < 0
⇒ k ∈ (0, 8)

Question 2.
Find a polynomial equation of minimum degree with rational coefficients, having 2 + √3 i as a root.
Solution:
Let the root be 2 + i √3
Another root be 2 – i √3
Sum of the roots = 2 + i √3 + 2 – i √3 = 4
Product of the roots = (2 + i √3) (2 – i √3) = 2² + √3² = 4 + 3 = 7
x² – (SR)x + PR = 0
x² – 4x + 7 = 0

Question 3.
Find a polynomial equation of minimum degree with rational coefficients, having 2i + 3 as a root.
Solution:
Given roots is (3 + 2i), the other root is (3 – 2i);
Since imaginary roots occur in with real co-efficient occurring conjugate pairs.
x² – x(S.O.R) + P.O.R = 0
⇒ x² – x(6) + (9 + 4) = 0
⇒ x² – 6x + 13 = 0

Question 4.
Find a polynomial equation of minimum degree with rational coefficients, having √5 – √3 as a root.
Solution:
Let the root be √5 – √3,
Another root is √5 + √3
Sum of the roots = √5 – √3 + √5 + √3 = 2√5
Product of roots = (√5 – √3) (√5 + √3)
√5² – √3² = 5 – 3 = 2
x² – (SR)x + PR = 0
x² – 2√5 x + 2 = 0 which is not rational co-efficient.
to make rational co-efficient
(x² + 2√5 x + 2) (x² + 2 + 2√5 x) = 0
(x² + 2)² – (2√5x)² = 0
x⁴ + 4 + 4x² – 20x² = 0
⇒ x⁴ – 16x² + 4 = 0 is a rational co-efficient polynomial equation.

Question 5.
Prove that a straight line and parabola cannot intersect at more than two points.
Solution:
Let the standard equation of parabola y² = 4ax …..(1)
Equation of line be y = mx + c …(2)
Solving (1) & (2)
(mx + c)² = 4ax
⇒ mx² + 2mcx + c² – 4ax = 0
⇒ mx² + 2x(mc – 2a) + c² = 0
This equation can not have more than two solutions and
hence a line and parabola cannot intersect at more than two points.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.1

Question 1.
If the sides of a cubic box are increased by 1, 2, 3 units respectively to form a cuboid, then the volume is increased by 52 cubic units. Find the volume of the cuboid.
Solution:
Let the side of the cube be ‘x’
Sides of cuboid are (x + 1) (x + 2) (x + 3)
∴ Volume of cuboid = x³ + 52
⇒ (x + 1) (x + 2) (x + 3) = x³ + 52
⇒ (x² + 3x + 2)(x + 3) = x³ + 52
⇒ x³ + 3x² + 3x² + 9x + 2x + 6 – x³ – 52 = 0
⇒ 6x² + 11x – 46 = 0 (÷2)
⇒ (x – 2) (6x + 23) = 0
⇒ x – 2 = 0 or 6x + 23 = 0
⇒ x = 2 or x = \(-\frac{23}{6}\) (not possible)
∴ x = 2
Volume of cube = 2³ = 8
Volume of cuboid = 52 + 8 = 60 cubic units

Question 2.
Construct a cubic equation with roots
Solution:
(i) 1, 2, and 3
α = 1, β = 2, γ = 3
α + β + γ = 6
αβ + βγ + γα = 2 + 6 + 3 = 11
αβγ = 6
x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ = 0
x³ – 6x² + 11x – 6 = 0

(ii) 1, 1, and -2
α = 1, β = 1, γ = -2
α + β + γ = 1 + 1 – 2 = 0
αβ + βγ + γα = 1 – 2 – 2 = -3
αβγ = 1(1)(-2) = -2
x³ – 0x² – 3x + 2 = 0
∴ x³ – 3x + 2 = 0

(iii) 2, \(\frac { 1 }{ 2 }\), and 1.

Multiplying by 2
2x³ – 7x² + 7x – 2 = 0

Question 3.
If α, β and γ are the roots of the cubic equation x³ + 2x² + 3x + 4 = 0, form a cubic equation whose roots are
(i) 2α, 2β, 2γ,
(ii) \(\frac{1}{α}\), \(\frac{1}{β}\), \(\frac{1}{γ}\)
(iii) – α, – β, – γ
Solution:
(i) Given that α, β, γ are the roots of x³ + 2x² + 3x + 4 = 0
Compare with x³ + bx² + cx + d = 0
b = 2, c = 3, d = 4
α + β + γ = -6 = -2
αβ + βγ + γα = c = 3
αβγ = -d = -4
Given roots are 2α, 2β, 2γ
2α + 2β + 2γ = 2 (α + β + γ)
= 2 (-2)
= -4
(2α) (2β) + (2β) (2γ) + (2γ) (2α) = (4αβ + 4βγ + 4γα)
= 4(αβ + βγ + γα)
= 4(3)
= 12
(2α) (2β) (2γ) = 8(αβγ)
= 8(-4)
= -32
The equation is
x³ – x² (2α + 2β + 2γ) + x (4αβ + 4βγ + 4γα) – 8 (αβγ) = 0
⇒ x³ – x² (-4) + x (12) – (-32) = 0
⇒ x³ + 4x² + 12x + 32 = 0

(ii) The new roots are \(\frac{1}{α}\), \(\frac{1}{β}\), \(\frac{1}{γ}\)

⇒ 4x³ + 3x² + 2x + 1 = 0

(iii) The given roots are -α, -β, -γ
The cubic equation is
x³ – x² (-α – β – γ) + x (αβ + βγ + γα) + (αβγ) = 0
⇒ x³ + x² (α + β + γ) + x (αβ + βγ + γα) + (αβγ) = 0
⇒ x³ + x² (-2) + x (3) – 4 = 0
⇒ x³ – 2x² + 3x – 4 = 0

Question 4.
Solve the equation 3x³ – 16x² + 23x – 6 = 0 if the product of two roots is 1.
Solution:
Let the roots be α, β, γ
Given αβ = 1, β = \(\frac{1}{α}\)

⇒ 3α² – 10α + 3 = 0
3α² – 9α – α + 3 = 0
3α(α – 3) -1(α – 3) = 0
(3α – 1) (α – 3) = 0
α = 3 or α = \(\frac{1}{3}\)
If α = 3, β = \(\frac{1}{3}\), γ = 2 (or)
α = \(\frac{1}{3}\), β = 3, γ = 2
⇒ [α, β, γ] = (\(\frac{1}{3}\), 3, 2)

Question 5.
Find the sum of squares of roots of the equation 2x⁴ – 8x³ + 6x² – 3 = 0.
Solution:
The given equation is 2x⁴ – 8x³ + 6x² – 3 = 0.
(÷ 2) ⇒ x⁴ – 4x³ + 3x² – \(\frac{3}{2}\) = 0
Let the roots be α, β, γ, δ
α + β + γ + δ = -b = 4
(αβ + βγ + γδ + αδ + αγ + βδ) = c = 3
αβγ + βγδ + γδα = -d = 0
αβγδ = \(\frac{-3}{2}\)
To Find α² + β² + γ² + δ² = (α + β + γ + δ)² – 2 (αβ + βγ + γδ + αδ + αγ + βδ)
= (4)² – 2(3)
= 16 – 6
= 10

Question 6.
Solve the equation x³ – 9x² + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3 : 2.
Solution:
Let the roots are 3α, 2α, β
sum of the roots are
3α + 2α + β = 9
5α + β = 9 ………. (1)
Product of two roots
3α(2α) + 2α(β) + β(3α) = 14
6α² + 5αβ = 14 ……… (2)
Product of three roots
(3α) (2α)β = -24
α²β = -4 ………. (3)
(1) ⇒ β = 9 – 5 α
(2) ⇒ 6α² + 5α (9 – 5α) = 14
6α² + 45α – 25α² = 14
-19α² + 45α – 14 = 0
19α² – 45α + 14 = 0
(α – 2) (α – \(\frac{7}{19}\)) = 0
α = 2 or α = \(\frac{7}{19}\)
If α = 2, β = 9 – 5 (α) = 9 – 5(2) = 9 – 10 = -1
roots are 3α, 2α, β
3(2), 2(2), -1 (i,e.,) 6, 4, -1
If α = \(\frac{7}{19}\), β = 9 – 5(\(\frac{7}{19}\)) = (\(\frac{136}{19}\))
roots are 3α, 2α, β (i,e.,) \(\frac{21}{19}\), \(\frac{14}{19}\), \(\frac{136}{19}\)

Question 7.
If α, β, and γ are the roots of the polynomial equation ax³ + bx² + cx + d = 0, find the value of Σ\(\frac{α}{βγ}\) terms of the coefficients.
Solution:

Question 8.
If α, β, γ and δ are the roots of the polynomial equation 2x⁴ + 5x³ – 7x² + 8 = 0, find a quadratic equation with integer coefficients whose roots are α + β + γ + δ and αβγδ.
Solution:

pq = (\(\frac{-5}{2}\))(4) = -10
x² – (p + q)x + pq = 0
x² – \(\frac{3}{2}\)x – 10 = 0
2x² – 3x – 20 = 0

Question 9.
If p and q are the roots of the equation lx² + nx + n = 0,
show that,
Solution:
p and q are the roots of the equation lx² + nx + n = 0
p + q = –\(\frac{n}{l}\), pq = \(\frac{n}{l}\)
LHS

Question 10.
If the equations x² + px + q = 0 and x² + p’x + q’ = 0 have a common root, show
that it must be equal to \(\frac{pq’-p’q}{q-q’}\) and \(\frac{q-q’}{p’-p}\)
Solution:
Let it be α common roots of x² + px + q = 0
x² + p’x + q’ = 0
(i,e.,) α² + pα + q = 0 …… (1) and
α² + p’α + q’ = 0 ………. (2)
Solving 1 and 2 by cross multiplication method, we have

Hence proved.

Question 11.
A 12-meter tall tree was broken into two parts. It was found that the height of the part which was left standing was the cube root of the length of the part that was cut away. Formulate this into a mathematical problem to find the height of the part which was cut away.
Solution:
Let the height of the tree = 12
length of the cut part = x³
Length of left out part = \(\sqrt[3]{x^{3}}\)
= x
Given x + x³ = 12
x³ + x – 12 = 0

Which is required mathematical problem

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.9 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.9

Choose the most suitable answer.

Question 1.
iⁿ + iⁿ⁺¹+ iⁿ⁺² + iⁿ⁺³ is:
(a) 0
(b) 1
(c) -1
(d) z
Solution:
(a) 0
Hint:
iⁿ + iⁿ⁺¹+ iⁿ⁺² + iⁿ⁺³
= iⁿ[1 + i + i² + i³]
= iⁿ[1 + i – 1 – i]
iⁿ (0) = 0

Question 2.
The value of \(\sum _{ i=1 }^{ 13 }{ ({ i }^{ n }+{ i }^{ n-1 }) } \) is
(a) 1 + i
(b) i
(c) 1
(d) 0
Solution:
(a) 1 + i
Hint:
\(\sum _{ i=1 }^{ 13 }{ ({ i }^{ n }+{ i }^{ n-1 }) } \)= (i¹ + i² + i³ + … + i¹³) + (i⁰ + i¹ + i² + … + i¹²)
= i⁰ + 2(i¹ + i² + i³  + ….. i¹²) + i¹³
= 1 + 2(i – 1 – i + 1 + … + 1) + 1
= 1 + 2(0) + i = 1 + i

Question 3.
The area of the triangle formed by the complex numbers z, iz, and z + iz in the Argand’s diagram is:
(a) \(\frac{1}{2}\) |z|²
(b) |z|²
(c) \(\frac{3}{2}\) |z|²
(d) 2|z|²
Solution:
(a) \(\frac{1}{2}\) |z|²
Hint:
Area of the triangle formed by the complex numbers z, iz and z + iz.
Let z = a + ib ⇒point (a, b)
iz = – b + ia ⇒ point (- b, a)
z + iz =(a – b) + i(a + b) point((a – b),(a + b))
Area of the triangle
= \(\frac {1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac {1}{2}\) [a(a – a – b) -b(a + b – b) + (a – b)(b – a)]
= \(\frac {1}{2}\) [-ab – ab + ab – a² – b² + ab]

Question 4.
The conjugate of a complex number is \(\frac{1}{i-2}\) Then, the complex number is:
(a) \(\frac{1}{i+2}\)
(b) \(\frac{-1}{i+2}\)
(c) \(\frac{-1}{i-2}\)
(d) \(\frac{1}{i-2}\)
Solution:
(b) \(\frac{-1}{i+2}\)
Hint:
Conjugate of complex number is \(\frac{1}{i-2}\)
∴ the complex number is \(\frac{-1}{i+2}\)

Question 5.
If z = \(\frac{(√3+i)^3(3i+4)²}{(8+6i)²}\)
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(c) 2
Hint:

Question 6.
If z is a non zero complex number, such that 2iz² = \(\bar { z }\) then | z | is:
(a) \(\frac{1}{2}\)
(b) 0
(c) 1
(d) 2
Solution:
z is a non zero complex number
Given 2iz² = \(\bar { z }\)
let z = x + iy
2i(x + iy)² = x – iy
simplifying 2i(x² – y² + 2ixy) = x – iy
-4xy + 2i(x² – y²) = x – iy
Equating real and imaginary parts
-4xy = x, 2(x² – y²) = -y
solving x = \(\frac{√3}{4}\), y =-\(\frac{1}{4}\)
z = \(\frac{√3}{4}\) – \(\frac{i}{4}\)
|z| = \(\sqrt { \frac{3}{16}+\frac{1}{16}}\) = \(\sqrt { \frac{1}{4}}\)
= \(\frac {1}{2}\)

Question 7.
If |z – 2 + i | ≤ 2, then the greatest value of |z| is:
(a) √3 – 2
(b) √3 + 2
(c) √5 – 2
(d) √5 + 2
Solution:
(d) √5 + 2
Hint:
|z – 2 + i | ≤ 2
|z + (-2 + i)| ≤ |z| + |-2 + i|
|z| ± √5
Given |z – 2 + i| ≤ 2
∴ |z| ± √5 ≤ 2
|z| ≤ 2 – √5. |z| ≤ 2 + √5
∴ The greatest value is 2 + √5

Question 8.
If |z – \(\frac{3}{2}\)| = 2 then the least value of |z| is:
(a) 1
(b) 2
(c) 3
(d) 5
Solution:
(a) 1
Hint:

|z|² – 2 |z| + 1 ≤ 3 + 1
(|z| – 1)² ≤ 4
|z| – 1 ≤ ± 2
|z| ≤ 2 + 1 and |z| ≤ – 2 + 1
|z| = -1
But |z| = 1

Question 9.
If |z| = 1, then the value of \( \frac { 1+z }{ 1+\bar { z } } \) is
(a) z
(b) \( \bar { z } \)
(c) \(\frac{1}{z}\)
(d) 1
Solution:
(a) z
Hint:

Question 10.
The solution of the equation |z| – z = 1 + 2i is:
(a) \(\frac{3}{2}\) – 2i
(b) – \(\frac{3}{2}\) + 2i
(c) 2 – \(\frac{3}{2}\)i
(d) 2 + \(\frac{3}{2}\)i
Solution:
(a) \(\frac{3}{2}\) – 2i
Hint:
|z| – z = 1 + 2i
Let z = x + iy
|z| = x + iy + 1 + 2i
\(\sqrt{x^2+y^2}\) = (x + 1) + i(y + 2)
\(\sqrt{x^2+y^2}\) = x + 1 y + 2 = 0
x² + y² = (x + 1)² y = -2
y² = 2x + 1
2x = 3
x = \(\frac{3}{2}\)
∴z = x + iy = \(\frac{3}{2}\) – 2i

Question 11.
If |z₁| = 1,|z₂| = 2, |z₃| = 3 and |9z₁z₂ + 4z₁z₃ + z₂z₃| = 12, then the value of |z₁ + z₂ + z₃| is:
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2
Hint:

Question 12.
If z is a complex number such that z∈C\R and z + \(\frac{1}{z}\) ∈R, then |z| is:
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:
If z ∈ C\R and z + \(\frac{1}{z}\) ∈ R
Then |z| = 1

Question 13.
z₁, z₂ and z₃ are complex numbers such that z₁ + z₂ + z₃ = 0 and |z₁| = |z₂| = |z₃| = 1 then \({ z }_{ 1 }^{ 2 }+{ z }_{ 2 }^{ 2 }+{ z }_{ 3 }^{ 2 }\) is
(a) 3
(b) 2
(c) 1
(d) 0
Solution:
(d) 0

Question 14.
If \(\frac{z-1}{z+1}\)is purely imaginary, then |z| is
(a) \(\frac{1}{2}\)
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:

Question 15.
If z = x + iy is a complex number such that |z + 2| = |z – 2|, then the locus of z is:
(a) real axis
(b) imaginary axis
(c) ellipse
(d) circle
Solution:
(b) imaginary axis
Hint:
|z + 2| = |z – 2|
Let z = x + iy
|(x + 2) + iy| = |(x – 2) + iy|
(x + 2)² + y² = (x – 2)² + y²
x² + 4x + 4 = x² – 4x + 4
⇒ x = 0

Question 16.
The principal argument of \(\frac{3}{-1+i}\) is:
(a) \(\frac{-5π}{6}\)
(b) \(\frac{-2π}{3}\)
(c) \(\frac{-3π}{4}\)
(d) \(\frac{-π}{2}\)
Solution:
(c) \(\frac{-3π}{4}\)
Hint:

Since Real and imaginary parts are negative.
‘θ’ lies in 3rd quadrant.
∴ Principal argument = – \(\frac {3π}{4}\) [∵ \(\frac {π}{4}\) – π]

Question 17.
The principal argument of (sin 40° + i cos 40°)⁵ is:
(a) – 110°
(b) -70°
(c) 70°
(d) 110°
Solution:
(a) – 110°
Hint:
z = (sin 40° + i cos 40°)⁵
= (cos 50° + i sin 50°)⁵
= cos 250° + i sin 250°]
= cos (360° – 110°) + i sin (360° – 110°)
= cos 110° – i sin 110°
= cos (-110°) + i sin (-110°)
∴ Principal argument is – 110°

Question 18.
If (1 + i) (1 + 2i) (1 + 3i) ……. (l + ni) = x + iy, then 2.5.10 …… (1 + n²) is:
(a) 1
(b) i
(c) x² + y²
(d) 1 + n²
Solution:
(c) x² + y²
Hint:
(1 + i) (i + 2i) ….. (1 + ni) = x + iy
Taking of two modulli of each of squaring
2.5.10 … (1 +n²) = x²+ y²

Question 19.
If ω ≠ 1 is a cubic root of unity and (1 + ω)⁷ = A + Bω, then (A, B) equals:
(a) (1, 0)
(b) (-1, 1)
(c) (0, 1)
(d) (1, 1)
Solution:
(d) (1, 1)
Hint:
(1 + ω)⁷ = A + Bω
(- ω²)⁷ = A + Bω
– ω¹⁴ = A + Bω
– ω² = A + Bω
1 + ω² = A + Bω
∴ A = 1, B = 1

Question 20.
The principal argument of the complex number \(\frac{(1+i \sqrt{3})^{2}}{4 i(1-i \sqrt{3})}\) is:
(a) \(\frac{2π}{3}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{5π}{6}\)
(d) \(\frac{π}{2}\)
Solution:
(d) \(\frac{π}{2}\)
Hint:

Question 21.
If α and β are the roots of x² + x + 1 = 0, then α²⁰²⁰ + β²⁰²⁰ is
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
(b) -1
Hint:
x² + x + 1 = 0

Question 22.
The product of all four values of (cos\(\frac{π}{3}\) + i sin \(\frac{π}{3}\))^{\(\frac{3}{4}\)} is:
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
(c) 1

Question 23.
If ω ≠ 1 is a cubic root of unity and

(a) 1
(b) -1
(c) √3 i
(d) -√3 i
Solution:
(d) -√3 i

= 1(ω² – ω⁴) – (ω – ω²) + 1(ω² – ω) = 3k
= ω² – ω – ω + ω² + ω² – ω = 3k
= 3ω² – 3ω = 3k
= 3(ω² – ω) = 3k
∴ k = ω² – ω

Question 24.
The value of (\(\frac{1+√3 i}{1-√3 i}\))¹⁰ is:
(a) cis\(\frac{2π}{3}\)
(b) cis\(\frac{4π}{3}\)
(c) -cis\(\frac{2π}{3}\)
(d) -cis\(\frac{2π}{3}\)
Solution:
(a) cis\(\frac{2π}{3}\)
Hint:

Question 25.
If ω = cis\(\frac{2π}{3}\), then the number of distinct roots of
(a) 1
(b) 2
(c) 3
(d) 4
Solution:


The expansion 1 becomes
z³ + (0) z² + (0) z + 0 = 0
⇒ z³ = 0
z = 0 is the only solution.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.8 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.8

Question 1.
If to ω ≠ 1 is a cube root of unity, then show that

Solution:
L.H.S

Question 2.
Show that

Solution:

Question 3.

Solution:


Aliter method:

Question 4.
If 2cos α = x + \(\frac{1}{x}\) and 2 cos β = y + \(\frac{1}{x}\), show that
(i) \(\frac{x}{y}+\frac{y}{x}=2 \cos (\alpha-\beta)\)
Solution:
Given 2 cos α = x + \(\frac{1}{x}\) and cos β = y + \(\frac{1}{y}\)
simplifying x² – 2x cos α + 1 = 0

if x = cos α + i sin α, then \(\frac{1}{x}\) = cos α – i sin α
similarly y = cos β + i sin β and \(\frac{1}{y}\) = cos β – i sin β

Hence proved

(ii) xy = (cos α + i sin α)(cos β + i sin β )
Solution:
xy = (cos α + i sin α) (cos β + i sin β)
= cos (α + β) + i sin (α + β)
[∵ arg (z₁z₂) = arg z₁ + arg z₂
\(\frac{1}{xy}\) = cos (α + β) – i sin (α + β)
∴ xy – \(\frac{1}{xy}\) = cos (α + β) + i sin (α + β) – cos (α + β) + i sin (α + β)
= 2i sin (α + β)
Hence proved

(iii) \(\frac{x^{m}}{y^{n}}-\frac{y^{n}}{x^{m}}\) = 2 i sin (mα – nβ)
Solution:

Hence Proved

(iv) x^m yⁿ + \(\frac { 1 }{ x^m y^n }\) = 2 cos(mα – nβ)
Solution:
= (cos mα + sin mα) (cos nβ + i sin nβ)
= cos (mα + nβ) + i sin (mα + nβ)

Hence proved

Question 5.
Solve the equation z³ + 27 = 0.
Solution:
z³ + 27 = 0
z³ = – 27 = 27 (-1)
= 27 [cos(π + 2kπ) + i sin(π + 2kπ)], k ∈ z
∴ z = (27)^1/3[cos (2k + 1)π + i sin (2k+1)π]^1/3 k ∈ z

Question 6.
If ω ≠ 1 is a cube root of unity, show that the roots of the equation (z – 1)³ + 8 = 0 are -1, 1 – 2ω, 1 – 2ω².
Solution:
Given ω ≠ 1 is a active root of unity
(z – 1)³ + 8 = 0
(z- 1)³ = -8
z – 1 = (-8)^1/3 (1)^1/3
= (-2) (1, ω, ω²)
z – 1 = (-2, -2ω, -2ω²)
= z – 1 = -2
z = -2 + 1 = -1
z – 1 = -2ω
z = 1 – 2ω
z – 1 = -2ω²
z = 1 – 2ω²

Question 7.

Solution:
\(\sum_{k=1}^{8}\) (cos \(\frac { 2kπ }{ 9 }\) + i sin \(\frac { 2kπ }{ 9 }\))
The sum all nth root of unity is
1 + ω + ω² + …….. + ω^n-1 = 0
From the given polar from , it is clear that the complex number is 1 + i0 (unity)

Question 8.
If ω ≠ 1 is a cube root of unity, show that
(i) (1 – ω + ω²)⁶ + (1 + ω – ω²)⁶ = 128.
Solution:
ω is a cube root of unity ω³ = 1; 1 + ω + ω² = 0
(1 – ω + ω²)⁶ + (1 + ω – ω²)⁶
= (-ω – ω)⁶ + (-ω² – ω²)⁶
= (-2ω)⁶ + (-2ω²)⁶
= (-2)⁶(ω⁶ + ω¹²)
= (64)(1 + 1)
= 128

(ii) (1 + ω) (1 + ω²) (1 + ω⁴) (1 + ω⁸)….. (1 + ω²ⁿ) = 1
Solution:
(1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸) …… (1 + ω²ⁿ)
= (1 + ω)(1 + ω²)(1 + ω⁴)(1 + ω⁸) ……. 2n factors
= (-ω²)(-ω)(-ω²)(-ω) …… 2n factors
= ω³. ω³
= 1
Hence proved.

Question 9.
If z = 2 – 2i, find the rotation of z by θ radians in the counterclockwise direction about the origin when
Solution:
Let 2 – 2i
Modules = |z| = \(\sqrt{2^2+2^2}\) = 2√2
Argument θ = tan^-1(\(\frac{-2}{2}\)) = tan^-1(-1) = –\(\frac{π}{4}\)
(i) when ‘z’ is rotated in the counter clockwise direction about the origin when θ = \(\frac{π}{3}\) i.,e argument of new position

(ii) θ = \(\frac{2π}{3}\)
Solution:

(iii) θ = \(\frac{3π}{3}\)
Solution:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.7 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7

Question 1.
Write in polar form of the following complex numbers.
(i) 2 + i2 √3
Solution:
Let z + i2√3 = r (cos θ + i sin θ)
equating real and imaginary parts
r cos θ = 2 (+ve)
r sin θ = 2√3 (+ve)
r² cos² θ + r² sin² θ = (2)² + (2√3)²
r² = 4 + 12 = 16
|z| = r = 4
since cos cos θ and sin θ are positive ‘θ’ lies in 1st quadrant.
cos θ = \(\frac{1}{2}\), sin θ = \(\frac{√3}{2}\)
∴ θ = sin θ = \(\frac{π}{3}\) (or) θ = tan^-1 |\(\frac{y}{x}\)|
= tan^-1 |\(\frac{2√3}{2}\)|
= tan^-1 √3 = \(\frac{π}{3}\)
∴ argument = 2kπ + \(\frac{π}{3}\)
∴ Polar form is z = r (cos θ + i sin θ)
2 + 2i√3 = 4 (cos (2kπ + \(\frac{π}{3}\)) + i sin(2kπ +\(\frac{π}{3}\))) k ∈ z

(ii) 3 – i √3
Solution:
Let z = 3 – i √3 = r (cos θ + i sin θ)
equating real and imaginary parts
r cos θ = 3 (+ve)
r sin θ = -√3 (-ve)
r² cos² θ + r² sin² θ = (3)² + (-√3)²
r² = 9 + 3 = 12
|z| = r = 2√3
since cos cos θ positive and sin θ in -ve so lies in IV quadrant.
cos θ = \(\frac{√3}{2}\), sin θ = \(\frac{-1}{2}\), θ = \(\frac{-π}{6}\)
argument = 2kπ – \(\frac{π}{6}\), k ∈ Z
polar from z = r(cos θ + i sin θ)
3 – i√3 = 2√3 (cos (2kπ – \(\frac{π}{6}\)) + i sin(2kπ – \(\frac{π}{6}\))) k ∈ Z

(iii) -2 – i 2 = r (cos θ + i sin θ)
Solution:
Let z = -2 – i2 = r(cos θ + i sin θ)
equating real and imaginary parts
r cos θ = -2
r sin θ = -2
r² cos² θ + r² sin² θ = (-2)² + (-2)²
r² = 4 + 4 = 8
r² = 8
|z| = r = 2√2
cos θ = \(\frac{-2}{2√2}\) = \(\frac{-1}{√2}\), sin θ = \(\frac{-2}{2√2}\) = \(\frac{-1}{√2}\)
since cos θ and sin θ both are in -ve so lies in III quadrant.
argument = 2kπ – 3\(\frac{π}{4}\)
as θ = \(\frac{π}{4}\) – π = –\(\frac{3π}{4}\)
polar from z = r(cos θ + i sin θ)
-2 – i2 = 2√2 (cos (2kπ – \(\frac{3π}{4}\)) + i sin(2kπ – \(\frac{3}{4}\))) k ∈ Z

(iv) \(\frac{i-1}{cos{\frac{π}{3}}+isin{\frac{π}{3}}}\)
Solution:

Question 2.
Find the rectangular form of the complex numbers

Solution:

Solution:

Question 3.
\(\left(x_{1}+i y_{1}\right)\left(x_{2}+i y_{2}\right)\left(x_{3}+i y_{3}\right) \cdots\left(x_{n}+i y_{n}\right)=a+i b\), show that

Solution:
Let (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n) = a + ib
Taking modulus
|(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n)| = |a + ib|
|x₁ + iy₁| |x₂ + iy₂| |x₃ + iy₃| …… |x_n + iy_n| = |a + ib|
\(\sqrt{x_{1}^{2}+y_{1}^{2}} \sqrt{x_{2}^{2}+y_{2}^{2}} \sqrt{x_{3}^{2}+y_{3}^{2}} \ldots \sqrt{x_{n}^{2}+y_{n}^{2}}\) = \(\sqrt{a^2+b^2}\)
Squaring on both sides
\(\left(x_{1}^{2}+y_{1}^{2}\right)\left(x_{2}^{2}+y_{2}^{2}\right)\left(x_{3}^{2}+y_{3}^{2}\right) \ldots\left(x_{n}^{2}+y_{n}^{2}\right)\) = a² + b²
Hence proved

(ii) \(\sum_{r=1}^{n}\) tan^-1 (\(\frac{y_r}{x_r}\)) = tan^-1 (\(\frac{b}{a}\)) + 2kπ, k ∈ Z
Solution:
Let (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n) = a + ib
Taking arguments
arg [(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …… (x_n + iy_n)] = arg (a + ib)
arg (x₁ + iy₁) + arg(x₂ + iy₂) + arg (x₃ + iy₃) …… + arg(x_n + iy_n) = arg(a + ib)

Question 4.
Given \(\frac{1+z}{1-z}\) = cos 2θ + i sin 2θ, show that To prove that z = i tan θ.
Solution:

Squaring on both sides
(1 + x)² + y² = (1 – x)² + y²
1 + 2x + x² + y² = 1 – 2x + x² +y²
x = 0
∴ z = 0 + iy = iy

∴ y = tan θ
hence z = iy
z = i tan θ

Question 5.
If cos α + cos β + cos γ = sin α + sin β + sin γ = 0. then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) and
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ).
Solution:
Let a = cos α + i sin α = e^iα
b = cos β + i sin β = e^iβ
c = cos γ + i sin γ = e^iγ
a + b + c = (cos α + cos β + cos γ) + i (sin α + sin β + sin γ)
⇒ a + b + c = 0 + i 0
⇒ a + b + c = 0
If a + b + c = 0 then a³ + b³ + c³ = 3abc

(cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ) = 3 [cos (α + β + γ) + i sin (α + β + γ)]
(cos 3α + cos 3β + cos 3γ) + i (sin 3α + sin 3β + sin 3γ) = 3 cos (α + β + γ) + i 3sin(α + β + γ)
Equating real and Imaginary parts
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)

Question 6.
If z = x + iy and arg \(\left(\frac{z-i}{z+2}\right)\) = \(\)\frac{π}{4}, then show that x² + y³ + 3x – 3y + 2 = 0.
Solution:

2y – x – 2 = x² + 2x + y² – y
x² + y² + 2x + x – y – 2y + 2 = 0
⇒ x² + y² + 3x – 3y + 2 = 0
Hence proved

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.6

Question 1.
If 2 = x + iy is a complex number such that \(\left|\frac{z-4 i}{z+4 i}\right|\) = 1 show that the locus of z is real axis.
Solution:
Let z = x + iy

Squaring on both sides
x² + (y – 4)² =  x² + (y + 4)²
simplifying
We get y = 0
Which is real axis

Question 2.
If z = x + iy is a complex number such that Im \(\left(\frac{2 z+1}{i z+1}\right)\) = 0, show that the locus of z is 2x² + 2y² + x – 2y = 0.
Solution:
Let z = x + iy

2y(1 – y) – x(2x + 1) = 0
⇒ 2y – 2y² – 2x² – x = 0
∴ The locus is 2x² + 2y² – 2y + x = 0
Hence proved

Question 3.
Obtain the Cartesian form of the locus of z = x + iy in each of the following cases:
(i) [Re (iz)]² = 3
Solution:
z = x + iy
[Re(iz)]² = 3
⇒ [Re[i(x + iy]]² = 3
⇒ [Re(ix – y)]² = 3
⇒ (-y)² = 3
⇒ y² = 3

(ii) Im[(1 – i)z + 1] = 0
⇒ Im [(1 – i)(z + iy) + 1] = 0
⇒ Im[x + iy – ix + y + 1] = 0
⇒ Im[(x + y + 1) + i(y – x)] = 0
Considering only the imaginary part
y – x = 0 ⇒ x = y

(iii) |z + i| = |z – 1|
⇒ |x + iy + i| = | x + iy – 1|
⇒ |x + i(y + 1)| = |(x – 1) + iy|
Squaring on both sides
|x + i(y + 1)|² = |(x – 1) + iy|²
⇒ x² + (y + 1)² = (x – 1)² + y²
⇒ x² + y² + 2y + 1 = x² – 2x + 1 + y²
⇒ 2y + 2x = 0
⇒ x + y = 0

(iv) \(\bar {z}\) = z^-1
Solution:

x² + y² = 1, x² + y² = -1 which cannot be true.
∴ x² + y² = 1

Question 4.
Show that the following equations represent a circle, and, find its centre and radius.
(i) |z – 2 – i| = 3
Solution:
Let z = x + iy
|z – 2 – i| = 3
⇒ |x + iy – 2 – i| = 3
⇒ |(x – 2) + i(y – 1)| = 3
⇒ \(\sqrt{(x-2)^{2}+(y-1)^{2}}=3\)
Squaring on both sides
(x – 2)² + (y – 1)² = 9
⇒ x² – 4x + 4 + y² – 2y + 1 – 9 = 0
⇒ x² + y² – 4x – 2y – 4 = 0 represents a circle
2g = -4 ⇒ g = -2
2f = -2 ⇒ f = -1
c = -4
(a) Centre (-g, -f) = (2, 1) = 2 + i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{4+1+4}=3\)
Aliter: |z – (2 + i)| = 3
Centre = 2 + i
radius = 3

(ii) |2(x + iy) + 2 – 4i| = 2
⇒ |2x + i2y + 2 – 4i| =2
⇒ |(2x + 2) + i(2y – 4)| = 2
⇒ |2(x + 1) + 2i(y – 2)| = 2
⇒ |(x + 1) + i(y – 2)| = 1
⇒ \(\sqrt{(x+1)^{2}(y-2)^{2}}=1\)
Squaring on both sides,
x² + 2x + 1 + y² + 4 – 4y – 1 = 0
⇒ x² + y² + 2x – 4y + 4 = 0 represents a circle
2g = 2 ⇒ g = 1
2f = -4 ⇒ f = -2
c = 4
(a) Centre (-g, -f) = (-1, 2) = -1 + 2i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-4}=1\)
Aliter: 2|(z + 1 – 2i)| = 2
|z – (-1 + 2i)| = 1
Centre = -1 + 2i
radius = 1

(iii) |3(x + iy) – 6 + 12i| = 8
⇒ |3x + i3y – 6 + 12i| = 8
⇒ |3(x – 2) + i3 (y + 4)| = 8
⇒ 3|(x – 2) + i (y + 4)| = 8
⇒ \(3 \sqrt{(x-2)^{2}+(y+4)^{2}}=8\)
Squaring on both sides,
9[(x – 2)² + (y + 4)²] = 64
⇒ x² – 4x + 4 + y² + 8y + 16 = \(\frac{64}{9}\)
⇒ x² + y² – 4x + 8y + 20 – \(\frac{64}{9}\) = 0
x² + y² – 4x + 8y + \(\frac{116}{9}\) = 0 represents a circle.
2g = -4 ⇒ g = -2
2f = 8 ⇒ f = 4
c = \(\frac{116}{9}\)
(a) Centre (-g, -f) = (2, -4) = 2 – 4i
(b) Radius = \(=\sqrt{g^{2}+f^{2}-c}=\sqrt{4+16-\frac{116}{9}}=\sqrt{\frac{180-116}{9}}=\frac{8}{3}\)
Aliter:
|z – 2 + 4i| = \(\frac{8}{3}\)
⇒ |z – (2 – 4i)| = \(\frac{8}{3}\)
Centre = 2 – 4i, Radius = \(\frac{8}{3}\)

Question 5.
Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases:
(i) |z – 4| = 16
Solution:
Let z = x + iy
|x + iy – 4| – 16
|(x – 4) + iy| = 16
\(\sqrt{(x – 4)² + y²}\) = 16
∴ Squaring on both sides
(x – 4)² + y² = 256
x² – 8x + 16 + y² – 256 = 0
x² + y² – 8x – 240 = 0
The locus of the point is a circle.

(ii) |z – 4|² – |z – 1|² = 16.
Solution:
|x + iy – 4|² – |x + iy – 1|² = 16
⇒ |(x – 4) + iy|² – |(x – 1) + iy|² = 16
⇒ [(x – 4)² + y²] – [(x – 1)² + y²] = 16
⇒ (x² – 8x + 16 + y²) – (x² – 2x + 1 + y²) = 16
⇒ x² + y² – 8x + 16 – x² + 2x – 1 – y² = 16
⇒ -6x + 15 = 16
⇒ 6x + 1 = 0
The locus of the point is a straight line.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.5

Question 1.
Find the modulus of the following complex numbers.
(i) \(\frac{2i}{3+4i}\)
Solution:

(ii) \(\frac{2-i}{1+i}+\frac{1-2 i}{1-i}\)
Solution:

Modulus of z = |z| = \(\sqrt{4+4}\)
= √8
= 2√2

(iii) |(1 – i)¹⁰| = (|1 – i|)¹⁰
= \((\sqrt{1+1})^{10}=(\sqrt{2})^{10}=2^{5}=32\)
(iv) |2i(3 – 4i) (4 – 3i)|
= |2i| |3 – 4i| |4 – 3i|
= \(2 \sqrt{9+16} \sqrt{16+9}\)
= 2 × 5 × 5
= 50

Question 2.
For any two complex numbers z₁ and z₂, such that |z₁| = |z₂| = 1 and z₁ z₂ ≠ -1, then show that \(\frac{z_{1}+z_{2}}{1+z_{1} z_{2}}\) is real number.
Solution:
Given |z₁| = |z₂| = 1 and z₁ z₂ ≠ 1
|z₁|² = 1 |z₂|² = 1
z₁ \(\bar{z}_{1}\) = 1 similarly z₂ \(\bar{z}_{2}\) = 1

Since z = \(\bar{z}\), it is a real number.

Question 3.
Which one of the points 10 – 8i, 11 + 6i is closest to 1 + i.
Solution:
A (1 + i), B (10 – 8i), C (11 + 6i)
|AB| = |(10 – 8i) – (1 + i)|
= |10 – 8i – 1 – i|
= |9 – 9i|
= \(\sqrt{81+81}\)
= \(\sqrt{162}\)
= 9(1.414)
= 12.726
CA = |(11 + 6i) – (1 + i)|
= |11 + 6i – 1 – i|
= |10 + 5i|
= \(\sqrt{100+25}\)
= \(\sqrt{125}\)
C (11 + 6i) is closest to the point A (1 + i)

Question 4.
If |z| = 3, show that 7 ≤ |z + 6 – 8i| ≤ 13.
Solution:
given |z| = 3
|z + 6 – 8i| ≤ |z| + |6 – 8i|
= 3 + \(\sqrt{6^2+8^2}\)
= 3 + \(\sqrt{100}\)
= 3 + 10 = 13
∴ |z + 6 – 8i| ≤ 13 ……….. (1)
|z + 6 – 8i| ≥ ||z| – |-6 + 8i||
= |3 – 10|
= |-7| = 7
∴ |z + 6 – 8i| ≥ 7 ………… (2)
from 1 and 2
we get 7 ≤ |z + 6 – 8i| ≤ 13
hence proved.

Question 5.
If |z| = 1, show that 2 ≤ |z² – 3| ≤ 4.
Solution:
|z| = 1 ⇒ |z|² = 1
||z₁| – |z₂|| ≤ |z₁ + z₂| ≤ |z₁| + |z₂|
||z|² – |-3|| ≤ |z² – 3| ≤ |z|² + |-3|
|1 – 3| ≤ |z² – 3| ≤ 1 + 3
2 ≤ |z² – 3| ≤ 4

Question 6.
If |z| = 2 show that the 8 ≤ |z + 6 + 8i| ≤ 12
Solution:
Given |z| = 2
|z + 6 + 8i| = |z| + |6 + 8i|
= 2 + \(\sqrt{6^2+8^2}\)
= 2 + \(\sqrt{100}\)
= 2 + 10
= 12
∴ |z + 6 + 8i| ≤ 12 ……….. (1)
|z + 6 + 8i| ≥ ||z| – |-6 – 8i||
= |2 – 10|
= |-8|
= 8
|z + 6 + 8i| ≥ 8 ………… (2)
From 1 and 2 we get
8 ≤ |z + 6 + 8i| ≤ 12
Hence proved

Question 7.
If z₁ z₂ and z₃ are three complex numbers such that |z₁| = 1, |z₁| = 2, |z₃| = 3 and |z₁ + z₂ + z₃| = 1 show that |9z₁ z₂ + 4z₁ z₃ + z₂ z₃| = 6.
Solution:
|z₁| = 1, |z₁| = 2, |z₃| = 3
|z₁ + z₂ + z₃| = 1
Now |9z₁ z₂ + 4z₁ z₃ + z₂ z₃|

Hence proved.

Question 8.
If the area of the triangle formed by the vertices z, iz, and z + iz is 50 square units, find the value of |z|.
Solution:
The given vertices are z, iz, z + iz ⇒ z, iz are ⊥r to each other.
Area of triangle = \(\frac { 1 }{ 2 }\) bh = 50
⇒ \(\frac { 1 }{ 2 }\) |z| |iz| = 50
⇒ \(\frac { 1 }{ 2 }\) |z| |z| = 50
⇒ |z|² = 100
⇒ |z| = 10
Aliter:
Given the area of triangle = 50 sq. unit

x² + y² = 100
|z|² = 100
|z| = 10

Question 9.
Show that the equation z³ + 2 \(\bar {z}\) = 0 has five solutions.
Solution:
Given z³ + 2 \(\bar {z}\) = 0
z³ = -2 \(\bar {z}\)
|z³| = |-2| |\(\bar {z}\)|
|z|³ = 2|z| [∵ |z| = |\(\bar {z}\)|
|z|³ – 2 |z| = 0
|z| [|z|² – 2] = 0
|z| = 0 |z|² = 2
z\(\bar {z}\) = 2
z = \(\frac{2}{\bar {z}}\) = ± √2 [∵ \(\bar {z}\) = \(\frac{-z^3}{2}\) ]
z = \(\frac{2}{(\frac{z^3}{-2})}\)
z⁴ = 4
It has 4 non zero solutions.
∴ Including z = 0 we have 5 solutions.

Question 10.
Find the square roots of
(i) 4 + 3i
Solution:
|4 + 3i| = \(\sqrt {4^2+3^2}\) = \(\sqrt {16+9}\)
\(\sqrt {25}\) = 5
Let \(\sqrt {4+3i}\) = a + ib
squaring on both sides
4 + 3i = (a + ib)²
4 + 3i = (a² – b²) + 2 jab
Equating real and imaginary parts
a² – b² = 4, 2ab = 3
(a² + b²)² = (a² – b²)² + 4a² b²
= (4)² + (3)²
= 16 + 9 = 25
∴ a² + b² = 5
Solving a² – b² = 4 and a² + b² = 5.
we get a² = \(\frac {9}{2}\) , b² = \(\frac {1}{2}\)
a = ±\(\frac {3}{√2}\) and b = ±\(\frac {1}{√2}\)
∴ \(\sqrt {4 + 3i}\) = a + ib
= ±(\(\frac {3}{√2}\) + ±\(\frac {i}{√2}\))
Aliter:
Square root of 4 + 3i
formula method

(ii) -6 + 8i
Solution:
Let \(\sqrt {-6 + 8i}\) = a + ib
Squaring on both sides
-6 + 8i = (a + ib)²
-6 + 8i = a² – b² + 2iab
Equating real and imaginary parts
a² – b² = -6 and 2ab = 8
Now (a² + b²)² = (a² – b²)² + 4a²b²
= (-6)² + (8)²
= 36 + 64 = 100
∴ a + b² = 10
Solving a² – b² = -6 and a² + b² = 10
we get 2a² = 4, b² = 8
a² = 2, b² = ±2√2
a = ±√2
∴ \(\sqrt {-6 + 8i}\) = ±√2 ± i 2√2
= ±(√2 + i 2√2)
Aliter:
square root of -6 + 8i
let a + ib = -6 + 8i
a = -6, b = 8

(iii) -5 – 12i
Solution:
Let \(\sqrt{-5-12 i}\) = a + ib
Squaring on both sides
-5 – 12i = (a+ib)²
-5 – 12i = a² – b² + 2iab
Equating real and imaginary parts
a² – b² = -5, 2ab = -12
(a² + b²)² = (a² – b²)² + 4a²b²
= (-5)² + (-12)² = 169
∴ a² + b² = 13
Solving a²- b² = -5 and a² + b² = 13
we get a² = 4, b² = 9
a = ±2, b = ±3
Since 2ab = -12 < 0, a, b are of opposite signs.
∴ When a = ±2, b = ±3
Now \(\sqrt{-5-12 i}\) = ± (2 – 3i)
Aliter
Square root of -5 – 12i
Let a + ib = -5 – 12i
a = -5, b = -12

Students can download 10th Social Science Economics Chapter 5 Industrial Clusters in Tamil Nadu Questions and Answers, Notes, Samacheer Kalvi 10th Social Science Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Social Science Solutions Economics Chapter 5 Industrial Clusters in Tamil Nadu

Samacheer Kalvi 10th Social Science Industrial Clusters in Tamil Nadu Text Book Back Questions and Answers

I. Choose the correct answer

Question 1.
‘The Detroit of Asia’ is
(a) Tuticorin
(b) Coimbatore
(c) Chennai
(d) Madurai
Answer:
(c) Chennai

Question 2.
Pumpsets and motors are produced mostly in …………….
(a) Salem
(b) Coimbatore
(c) Chennai
(d) Dharampuri
Answer:
(b) Coimbatore

Question 3.
Tuticorin is known as:
(a) Gateway of India
(b) Gateway of Tamil Nadu
(c) Pump city
(d) None of these
Answer:
(b) Gateway of Tamil Nadu

Question 4.
……………… are an essential aspect of a nation’s development.
(a) Agriculture
(b) Industry
(c) Railway
(d) none of these
Answer:
(a) Agriculture

Question 5.
Tiruppur is known for:
(a) Leather tanning
(b) Lock making
(c) Knitwear
(d) Aigo-processing
Answer:
(c) Knitwear

Question 6.
Along with Ambur and Vaniyambadi ………….. is also a centre for leather goods exports.
(a) Chennai
(b) Sivakasi
(c) Coimbatore
(d) Madurai
Answer:
(a) Chennai

Question 7.
IT means
(a) Indian Technology
(b) Information Technology
(c) Institute of Technology
(d) Initiative Technology
Answer:
(b) Information Technology

Question 8.
A successful industrial cluster entirely created by the Tamil Nadu is ………………
(a) Hosur
(b) Dindigul
(c) Kovilpatti
(d) Thirunelveli
Answer:
(a) Hosur

Question 9.
SIPCOT was formed in the year:
(a) 1972
(b) 1976
(c) 1971
(d) 1978
Answer:
(c) 1971

Question 10.
Which is the Tamil Nadu Industrial Development Agency?
(a) SIPCOT
(b) TANSIDCO
(c) TIDCO
(d) all of these
Answer:
(d) all of these

II. Fill in the blanks

1. ………….. are very important in the modern economic activates of man.
2. ………….. are groups of firms in a defined geographic area that share common market and technologies.
3. Hundred of leather and tannery facilities are located around ………….. District inTamilNadu.
4. ………….. is fondly calls as ‘Little Japan’.
5. Special Economic Zones policy was introduced on in …………..
6. ………….. is an innovator of new ideas and business processes.

Answers:

1. Industrialisation
2. Industrial Clusters
3. Vellore
4. Sivakasi
5. April 2000
6. Entrepreneur

III. Choose the correct statement

Question 1.
(i) Entrepreneurship promotes capital formation by mobilising the idle saving of the public.
(ii) They are not provide large scale employment to artisan, technically qualified persons and professionals.
(iii) Entrepreneurs help the country to increase the GDP and per capitals income.
(iv) Entrepreneurs not promote country’s export trade.
(a) (i) and (iv) is correct
(b) (i) only correct
(c) (iii) and (iv) is correct
(d) (i) and (iii) is correct
Answer:
(d) (i) and (iii) is correct

IV. Pick out odd one

Question 1.
Which one of the following is not having leather factories?
(a) Ranipet
(b) Bharmapuri
(c) Ambur
(d) Vaniyambadi
Answer:
(b) Bharmapuri

Question 2.
Which one of the following is not a industrial developing agency?
(a) TIDCO
(b) SIDCO
(c) MEPG
(d) SIPCOT
Answer:
(c) MEPG

V. Match the following

Answer:
A. (iii)
B. (i)
C. (iv)
D. (v)
E. (ii)

VI. Write Short Answer

Question 1.
Why should a developing economy diversify out of agriculture?
Answer:
As an economy grows and incomes increase, consumers tend to spend a lesser share of their income on products from the agricultural sector. There are limits to the ability of agriculture to absorb labour due to the declining marginal productivity of land. Due to this, there is a need for an economy’s production and employment base to diversity away from agriculture.

Question 2.
Why are wages low in the agricultural sector?
Answer:
Labour productivity cannot increase in the agricultural sector as the marginal productivity of land goes on decreasing. Therefore wages remain low resulting in poverty.

Question 3.
What is meant by an industrial cluster?
Answer:
Industrial clusters are groups of firms in a defined geographic area that share common markets, technologies and skill requirements. An important aspect of clusters is the nature of inter-firm networks and interactions.

Question 4.
What are the routes for cluster formation?
Answer:

1. When artisans settle in one region and slowly spread their art in other regions.
2. When a large firm is established, to take care of its inputs and service requirements a cluster of firms may emerge.
3. Governments initiative to encourage Industrial sector using raw materials from a region.

Question 5.
Mention the 3 areas of policy-making that helped Tamil Nadu become one of the most industrialised states in the country.
Answer:
(a) Tamilnadu Industrial Policy – 2014
(b) Tamilnadu SEZs Policy
(c) Tamilnadu Biotechnology Policy – 2014

Question 6.
Mention any three-industrial development agencies in Tamil Nadu and their role.
Answer:
SIPCOT – State Industries Promotion Corporation of Tamil Nadu.

To promote Industrial growth by setting up Industrial Estates.

TIIC – Tamil Nadu Industrial Investment Cooperation Limited

To provide low – cost financial support for both setting up new firms and also to expand.

TIDCO – Tamil Nadu Industrial Development Corporation.

To promote Industrial growth by setting up Industrial Estate

Question 7.
What are the problems of industrialization currently in Tamil Nadu?
Answer:
To begin with, some clusters, especially chemicals, textiles and leather clusters, tend to generate a lot of polluting effluents that affect health. The effluents also pollute water bodies ‘ into which effluents are let into and also adjoining agricultural lands.

Second, employment generation potential has declined because of use of frontier technologies because of the need to compete globally. Quality of employment also has suffered in recent years as most workers are employed only temporarily. This issue too requires urgent attention among policymakers.

Question 8.
What is Meant by Entrepreneur?
Answer:
Entrepreneur is the person one who possess management skills, strong team building abilities and essential leadership qualities to manage a business.

Question 9.
What is Entrepreneurship?
Answer:
Entrepreneurship is a process of an action of an entrepreneur who undertakes to establish his entreprise. It is the ability to create and build something.

VII. Write brief Answer

Question 1.
What are the contributions of industrialization to development?
Answer:

1. Industries contribute by producing inputs such as fertilizers and tractors to agriculture thereby help them to increase productivity.
2. Services like Banking, transport and trade are dependent on the production of Industrial goods.
3. By using modem methods of production Industries contribute to better productivity and hence lower cost of production:
4. Industries helps to absorb the labour force coming out of agriculture.
5. By using modem technology, labour productivity increases, which help workers to get higher wages.
6. Increased income of the people lead to more demand for goods and services.
7. By producing more Industrial products, exports increases, thereby generate more foreign exchange.

Question 2.
Write a note on history of industrialisation in Tamil Nadu.
Answer:
Industrialisation in the Colonial Period

• The introduction of cotton cultivation in western and southern Tamil Nadu by the colonial government led to the emergence of a large-scale textile sector in these parts, which involved ginning, pressing, spinning and weaving operations.
• Introduction of railways also expanded the market for cotton yam and helped develop the sector.
• There was increase in trade during this period which led to industrial development. The two active ports in the region were Chennai and Tuticorin.
• In Western Tamil Nadu, the emergence of textiles industries also led to demand and starting
  of textile machinery industry in the region.

Post-Independence to early 1990s:

• After independence, several large enterprises were set up by both the central and state governments.
• The Integral Coach Factory in Chennai made railway coaches and the Bharat Heavy Electricals Limited (BHEL) in Tiruchirapalli manufactured boilers and turbines.
• Ashok Motors and Standard Motors together helped form an automobile cluster in the Chennai region.
• The 1970s and 1980s saw the setting up of emergence of power loom weaving clusters in the Coimbatore region as well as expansion of cotton knitwear cluster in Timppur and home furnishings cluster in Kamr.
• The Hosur industrial cluster is a successful case of how such policy efforts to promote industrial estates helped develop industries in a backward region.

Industrialization in Tamil Nadu – Liberalization Phase:

• The final phase of industrialisation is the post-reforms period since the early 1990s.
• Because of trade liberalisation measures, exports of textiles, home furnishings and leather products began to grow rapidly.
• Efforts to attract investments led to entry of leading multinational firms (MNCs) into the state, especially in the automobile sector.
• Chennai region also emerged as a hub for electronics industry with MNCs such as Nokia, Foxconn, Samsung and Flextronics opening plants on the city’s outskirts.
• A significant share of these investments has come up in special economic zones in the districts bordering Chennai.
• The major industries are automobiles, autocomponents, light and heavy engineering, machinery, cotton, etc.
• This diffused process of industrialisation and corresponding urbanisation has paved the way for better rural-urban linkages in Tamil Nadu than in most other states.

Question 3.
What are the important characteristics of successful industrial clusters? .
Answer:
The following are the chief characteristics of a successful cluster.

1. Geographical proximity of Small and Medium Enterprises (SMEs)
2. Sectoral specialisation
3. Close inter firm collaboration
4. Inter – firm competition based on innovation
5. A Socio – Cultural Identity which facilitates trust.
6. Multi – skilled workforce
7. Active self – help organisations and
8. Supportive regional and municipal governments.
9. Through Competition, they are forced to become more efficient.

Question 4.
Write about the Textile industry cluster in Tamil Nadu?
Answer:
Textile Clusters:
Tamil Nadu is home to the largest textiles sector in the country. Because of the development of cotton textile industry since the colonial period, Coimbatore often referred as the “Manchester of South India”. At present, most of the spinning mills have moved to the smaller towns and villages at a radius over 100 to 150 km around the Coimbatore city. Tamil Nadu is the biggest producer of cotton yam in the country.

Palladam and Somanur, small towns near Coimbatore and the villages near these towns, are home to a dynamic powerloom weaving cluster as well. Powerloom is however more widespread with Erode and Salem region too having a large number of power loom units.

Tiruppur is famous for clustering of a large number of firms producing cotton knitwear. It accounts for nearly 80% of the country’s cotton knitwear exports and generates employment in the range of over three lakh people since the late 1980s. It is also a major producer for the domestic market. Because of its success in the global market, it is seen as one of the most dynamic clusters in the Global South. While initially most firms were run by local entrepreneurs, at present, some of the leading garment exporters in India have set up factories here.

Apart from body building, Karur is a major centre of exports of home furnishings like table cloth, curtains, bed covers and towels. Bhavani and Kumrapalayam are again major centres of production of carpets, both for the domestic and the global markets.

Apart from such modem clusters, there are also traditional artisanal clusters such as Madurai and Kanchipuram that are famous for silk and cotton handloom sarees. Even these clusters have witnessed a degree of modernisation with use of powerlooms in several units.

Question 5.
Write in detail about the types of policies adopted by the Tamil Nadu government to industrialise.
Answer:
The type of policies that are adopted by the Tamil Nadu Government to Industrialise are:- Education, Infrastructure, and Industrial promotion.

(i) Education: Industries require skilled human resources. Therefore, labourers are given technical knowledge apart from basic skills to enrich themselves. Many engineering colleges, polytechnics and Industrial training centres are opened in the country.

(ii) Infrastructure: Excellent infrastructure facilities has contributed to the spread of Industrialisation in smaller towns and villages in the state. Rural electrification, transport and especially minor roads that connect rural parts of the State enabled vast Industrialisation.

(iii) Industrial Promotion: Policies to promote specific sectors like automobile, auto components, bio – technology and information and communication sectors have been formulated to promote Industries of the state.

Question 6.
Explain the role of Entrepreneur?
Answer:
Role of an Entrepreneur:
Entrepreneurs play a most important role in the economic growth and development of a country’s economy.

1. They promote development of industries and help to remove regional disparities by industrialising rural and backward areas.
2. They help the country to increase the GDP and Per Capita Income.
3. They contribute towards the development of society by reducing concentration of income and wealth.
4. They promote capital formation by mobilising the idle savings of the citizens and country’s export trade.
5. Entrepreneurs provide large-scale employment to artisans, technically qualified persons and professionals and work in an environment of changing technology and try to maximise profits by innovations.
6. They enable the people to avail better quality goods at lower prices, which results in the improvement of their standard of living.

VIII. Case studies

Question 1.
Choose a cluster in Tamil Nadu based on online research and write a note on it.
Answer:
An example of a cluster in Tamil Nadu is given below. Students can do online research on their own and write details using this as a sample.

Example case study of a pulp and paper industry in Tamil Nadu.

Tamil Nadu Newprint and papers Limited (http:// www.tnpl.co.in/)

The company: TNPL was formed by the Government of India in 1979 as a public limited company under the provisions of the companies Act of 1956. Objective: The primary objective of the company is to produce newsprint and printing and writing paper using bagasse, a sugarcane residue as the primary raw material.

Assistance: The only paper will in India assisted by the World Bank.

Machinery: The state of art machines were built in flexibility for manufacturing both newsprint and printing and writing papers in the same machine.

Capacity: The latest upgraded capacity enhanced to 2,30,000 tpa in April 2003 through upgradation of the paper machines which is considered as the largest production capacity in India at a single location.

Marketing: The products are being marketed throughout the country and also exported to 20 countries around the world.

Location: The factory is situated at Kagithapuram in Kanir district in Tamil Nadu.

IX. Activity and Project

Question 1.
Write a note on a cluster or a firm near your school/home based on your observations.
Answer:
Here is an sample of a cluster of firm observed in an area is given. This is to help students gain a basic idea about how to undertake this activity. Students can select their location, observe and write findings and do this activity.

Name of the Village: Neikkarapatti, Salem

Industrial cluster: Good quality and high production of Jaggery. The area in around almost all the houses, small or big make it a point to involve themselves in the production of Jaggery.

Type: It is one of the prominent Cottage Industry in the area.

Reason: Most of the farmers in the region cultivate sugarcane and own a jaggery making unit.

Labour: It is a manual jaggery making traditional work, unmindful of the challenges.

Process: The whole process takes about five hours with different names locally as Vellam and Mandai Vellam based on the shape of the mould.

X. Life Skills

Question 1.
Teacher and Students discuss about the entrepreneurs and their activities and Write an a essay in the topic of “If you are like a Entrepreneur”.
Answer:
Note: Students should imagine themselves as entrepreneurs and write an essay on the topic. This is sample essay given as a guideline for the students.

(A stationery shop – business)

Entrepreneurs are business owners. If I am a entrepreneur, first of all, I should start my business in the line of my interest and in part with the demand of the locality and their needs. This would help me to earn profit from it.

I prefer do my entrepreneurial task by staring it at a small level with less financial investment (approx. 10,000) from my uncle who is also an entrepreneur who supports and motivates me.

I purchase my products for sale from the whole saler. The items I purchase are not perishable stationery items. It is easy for me to store it in my house itself. I get bulk orders from nearby shops. Sometimes, latest arrivals of designed erasers, pencil sharpeners will be a attractive one.

As an entrepreneur, I am ready to face risk factors, price hike, less demand, poor quality, seasonal changes and so on. But, I enjoy my work as a businessman and earn profit that gives my career a spark to continue in the same line of business.

Samacheer Kalvi 10th Social Science Industrial Clusters in Tamil Nadu Additional Important Questions and Answers

I. Choose the correct answer

Question 1.
The conversion of raw materials into usable materials is called as
(a) Entrepreneur
(b) Industry
(c) Exports
(d) Clusters
Answer:
(b) Industry

Question 2.
Wind energy is a form of …………… energy.
(a) Solar
(b) Petrol
(c) Hydel
Answer:
(a) Solar

Question 3.
SMESare:
(a) Small and Medium Enterprises
(b) Small, Medium, Export Services
(c) Small and Medium Export Services
(d) Salem Metal Export Services.
Answer:
(a) Small and Medium Enterprises

Question 4.
TIDCo is another government agency to establish ………………. estates.
(a) Industrial
(b) tea
(c) Real
Answer:
(a) Industrial

Question 5.
The Namakkal -Tiruchengode belt in Western Tamil Nadu is known for its ………………. building industry.
(a) Textile
(b) Truck body
(c) Coach
(d) Steel
Answer:
(b) Truck body

Question 6.
MEPZ is a special Economic zone in …………….
(a) Chennai
(b) Trichy
(c) Tirunelveli
Answer:
(a) Chennai

Question 7.
TANS! was formed in the year:
(a) 1945
(b) 1955
(c) 1965
(d) 1975
Answer:
(c) 1965

Question 8.
………………. is an innovator of new ideas in business.
(a) Agriculturalist
(b) Entrepreneur
(c) Both (a) and (b)
(d) None
Answer:
(b) Entrepreneur

Question 9.
There are limits to the ability of agriculture to absorb labour due to the ………………. marginal productivity of land.
(a) Increasing
(b) Decreasing
(c) Steady
(d) None
Answer:
(b) Decreasing

Question 10.
Health care and educational services are diffused across major cities of:
(a) Chennai
(b) Coimbatore
(c) Both (a) and (b)
(d) Tiruppur
Answer:
(c) Both (a) and (b)

Question 11.
Nanguneri SEZ is situated at:
(a) Tiruvallur
(b) Vayalur
(c) Thirunelveli
(d) Tambaram
Answer:
(c) Thirunelveli

Question 12.
………………. is intended to provide low – cost financial support for both setting up of new units and for expansion of existing units.
(a) TIDCO
(b) TANSI
(c) TIIC
(d) MEPZ
Answer:
(c) TIIC

Question 13.
When Government decide to encourage manufacturing using raw material from a region. It may lead to emergence of:
(a) Industrial clusters
(b) More taxation
(c) Subsidy
(d) Both (a) and (b)
Answer:
(a) Industrial clusters

Question 14.
The notion of an “Industrial district” was developed by Prof:
(a) Adam Smith
(b) Marshall
(c) Samuelson
(d) Pigou
Answer:
(b) Marshall

Question 15.
Heavy vechicles factory was set up to manufacture tanks in:
(a) Peramber
(b) Avadi
(c) Tiruchy
(d) Vellore
Answer:
(b) Avadi

Question 16.
Dindigul, Vellore and Amber area are famous for products.
(a) Rice
(b) Wheat
(c) Leather
(d) Marine
Answer:
(c) Leather

Question 17.
The Avadi Industrial Estate was set up in the year:
(a) 1950
(b) 1960
(c) 1970
(d) 1980
Answer:
(a) 1950

Question 18.
IT (Information Technology) Specific Special Economic Zones are located in ………………. locations in Tamil Nadu.
(a) 6
(b) 7
(c) 8
(d) 10
Answer:
(c) 8

Question 19.
The agencies that is formed to promote Industrial growth in the state by setting up Industrial estates are:
(a) SIPCOT
(b) TIDCO
(c) TIIC
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 20.
Over the last ten years a few software firms have moved from Chennai to:
(a) Madurai
(b) Bangalore
(c) Coimbatore
(d) None
Answer:
(c) Coimbatore

II. Fill in the blanks

1. Stand up India scheme was launched in India in the year
2. ………….. is the ability to create and built something.
3. The Industries that produce raw materials for other Industries are called ………….. Industries.
4. If the output is consumed by another producer then, it is called as ………….. goods.
5. Geographical proximity of small and medium enterprise is a chief characteristic of a ………….. cluster.
6. ………….. policies have contributed to the decline of the handloom weaving industry.
7. The Salem steel plant was set up in the year …………..
8. Home Furnishings cluster is located at …………..
9. Integral Coach Factory (ICF) makes …………..
10. MNC means …………..
11. There are ………….. clusters in 13 districts of Tamil Nadu.
12. Transportation and poultry clusters are located in …………..
13. ………….. located in Trichy manufactures Boilers and Turbines.
14. The ………….. district is the top exporter of finished leather goods in the country.
15. SIPGOT was formed in the year …………..
16. MEPZ was established in the year to promote foreign direct investment.
17. A policy was set up in the year ………….. for setting up special Economic zone.
18. TANSI was formed in the year …………..
19. The poison control centre is associated with ………….. SEZ.
20. ………….. is the first Industrial cooperation operating in the domain of small enterprises.
21. There are ………….. export processing zones in the country set up by the Central Government.
22. ………….. schemes provides financial help specifically to SC and ST borrower and woman borrower.
23. Start up India scheme was launched to generate ………….. and creating …………..

Answers:

1. 5^th April 2016
2. Entrepreneur
3. Basic goods
4. capital
5. successful
6. Colonial
7. 1973
8. Karur
9. Railway coaches
10. Multi – National Companies
11. 27
12. Namakkal
13. BHEL
14. Vellore
15. 1971
16. 1984
17. 2000
18. 1965
19. Bio – pharmaceuticals
20. TANSI
21. Seven
22. Standup India
23. employment, wealth

IV. Choose the correct statement

Question 1.
(i) The development of Industries in India can be studied under colonial phase, post independent phase and liberalisation phase.
(ii) Services sector contributes a major share in employment generation.
(iii) Karur is expertised in bus body building and home furnishing.
(iv) Tamil Nadu is the biggest producer of cotton yarn in the country.
(a) (i), (ii) are correct
(b) (iii), (iv) are correct
(c) (i), (iii), (iv) are correct
(d) all are correct
Answer:
(d) all are correct

Question 2.
(i) Only after the economic reforms in 1990 the state has been the entry of hardware and electronic manufacture centres.
(ii) Bhavani and Kumarapalayan are major centres of production of carpets locally and globally.
(iii) Sivakasi region has now become a major centre for printing and fireworks in the country.
(iv) Dindigul and Erode are major employment generators in Knitwear industry.
(a) (i), (ii) are correct
(b) (i), (ii), (iii) are correct
(c) only (ii) and (iv) correct
(d) All are correct
Answer:
(b) (i), (ii), (iii) are correct

V. Pick out odd one

Question 1.
Which is not a export processing zone?
(a) MEPZ
(b) SEZ
(c) TIDCO
(d) ELCOT
Answer:
(c) TIDCO

Question 2.
Tamil Nadu’s Textile clusters does not include
(a) Coimbatore
(b) Padalam
(c) Somanur
(d) Dindigul
Answer:
(d) Dindigul

Question 3.
Which of the following is not under IT cluster?
(a) Nokia
(b) Foxconn
(c) Infosys
(d) MEPZ
Answer:
(d) MEPZ

VI. Write Short Answer

Question 1.
What is the industry?
Answer:
“Any human activity which is engaged in the conversion of raw materials into readily usable materials is called an industry”.

Question 2.
Why is small scale sectors considered important?
Answer:
The small scale sector is seen as important for two reasons.

1. To generate more employment than the large – scale sector.
2. The small scale sectors allows for a larger number of entrepreneurs to emerge from less privileged groups.

Question 3.
What is MEPZ?
Answer:
MEPZ is a special Economic Zone in Chennai and it is one of the seven export processing zones in the country set up by the central government. It was established in 1984. The MPEZ head-quarters is located on GST Road in Tambaram, Chennai.

Question 4.
Write the names of MNCs in Chennai region.
Answer:
MNCs such as Nokia, Foxconn, Samsung and Flextronics.

Question 5.
Write about Bus Body Building Industry clusters.
Answer:
The Namakkal-Tiruchengode belt in western Tamil Nadu is known for its truck body building industry. About 150 of the 250 units in this sector are located in this cluster including 12 large-sized body building houses. Karur is another major hub with more than 50 units. Many entrepreneurs were previous employees in a big firm involved in body building who came out . to set up their own units.

Question 6.
List down the names of the agencies that have played an important role in the Industrialisation of a state.
Answer:

1. SIPCOT – State Industries Promotion Corporation of Tamil Nadu.
2. TANSIDCO – Tamil Nadu Small Industries Development Corporation.
3. TIDCO – Tamil Nadu Industrial Development Corporation
4. TIIC – Tamil Nadu Industrial Investment Corporation Limited.
5. TANSI – Tamil Nadu Small Industries Corporation Limited.

Question 7.
What is meant by SEZ?
Answer:
SEZ means Special Economic Zone in the country with a view to improve free environment for exports.

Question 8.
What do you understand by Stand up India Scheme?
Answer:
It is a scheme launched by the Indian Government with the primary objective of generation employment and wealth creation.

Question 9.
What do you understand by standup India scheme?
Answer:
It is a scheme launched by the Indian Government to facilitate bank loans between ₹ 10 lakh and ₹ 1 crore to atleast one scheduled caste (or) scheduled Tribe borrower and one woman borrower per bank branch for setting up a greenfield enterprise.

Question 10.
How do entrepreneurs promote formation?
Answer:
Entrepreneurs promote capital formation by mobilising the idle savings of the citizens and increasing country’s exports.

VII. Write Brief Answer

Question 1.
Write in detail about the types of industries on the basis of its use, raw ‘ material, ownership, and size.
Answer:
Types of Industries:

On the basis of

Uses:
Consumer goods Industries ⇒ output to the final consumer
Capital goods Industries ⇒ output consumed by another producer.
Basic goods Industries ⇒ output as the raw material for other Industries.

Raw material:
Agricultural sector
Industrial sector
Agro based sector
Leather Industries

Ownership:
Public owned ⇒ Government owned
Private owned ⇒ Private owned Co-operative owned

Size:
Large scale Industries
Small scale Industries
Medium scale Industries
Micro (or) tiny

Question 2.
Name some industrial development agencies and explain them.
Answer:
The following are some agencies that have played a key role in industrialization in the state. SIPCOT: (State Industries Promotion Corporation of Tamil Nadu), 1971 It was formed in the year 1971 to promote industrial growth in the state by setting up industrial estates.

TANSIDCO: (Tamil Nadu Small Industries Development corporation), 1970
TANSIDCO is a state-agency of the state of TN established in the year 1970 to promote small- scale industries in the state. It gives subsidies and provide technical assistance for new firms in the small scale sector.

TIDCO (Tamil Nadu Industrial Development Corporation), 1965:
TIDCO is another government agency to promote industries in the state and to establish industrial estates.

TIIC (Tamil Nadu Industrial Investment Corporation Ltd.), 1949:
TIIC is intended to provide low-cost financial support for both setting up new units and also for expansion of existing units. Though it is meant to meet the requirements of all types of firms, 90% of support goes to micro, small and medium enterprises.

TANSI (Tamil Nadu Small Industries Corporation Ltd.), 1965:
TANSI was formed in 1965 to take over the small scale-units that were set up and run by the Department of Industries and Commerce. It is supposed to be the first industrial corporation operating in the domain for small enterprises.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.4

Question 1.
Write the following in the rectangular form:
(i) \(\overline { (5+9i)+(2-4i) } \)
Solution:
\(\overline { (5+9i)+(2-4i) } \)
= \(\overline {(5+9i)} \) + \(\overline {(2-4i)} \)
= 5 – 9i + 2 + 4i
= 7 – 5i

(ii) \(\frac {10-5i}{6+2i} \)
Solution:

(iii) \(\overline {3i} + \frac{2}{2-i}\)
Solution:

Question 2.
If z = x + iy, find the following in rectangular form.
(i) Re(\(\frac {1}{z} \))
Answer:

(ii) Re(i\(\bar{z}\)) = Re[i(\(\overline{x+i y}\))]
= Re(ix + y)
= y
(iii) Im(3z + 4\(\bar{z}\) – 4i)
= Im (3(x + iy) + 4(x – iy) – 4i)
= Im (3x + 3iy + 4x – 4iy – 4i)
= Im (3x + 4 + i (3y – 4y – 4)
= Im (3x + 4x + i(-y – 4))
= Im [7x + i(-y – 4)]
= -y – 4
= -(y + 4)

Question 3.
If z₁ = 2 – i and z₂ = -4 + 3i, find the inverse of z₁, z₂ and \(\frac {z_1}{z_2} \)
Solution:
z₁ = 2 – i, z₂ = -4 + 3i
z₁ z₂ = (2 – i) (-4 + 3i)
= -8 + 3 + 4i + 6i
= -5 + 10i

Question 4.
The complex numbers u, v, and w are related by \(\frac {1}{u}\) = \(\frac {1}{v}\) + \(\frac {1}{w}\). If v = 3 – 4i and w = 4 + 3i, find u in rectangular form.
Solution:
v = 3 – 4i, w = 4 + 3i

Question 5.
Prove the following properties:
(i) z is real if and only if z = \(\overline {z}\)
Solution:
z is real iff z = \(\bar{z}\)
Let z = x + iy
z = \(\bar{z}\)
⇒ x + iy = x – iy
⇒ 2iy = 0
⇒ y = 0
⇒ z is real.
z is real iff z = \(\bar{z}\)

(ii) Re(z) = \(\frac{z+\bar{z}}{2}\) and Im(z) = \(\frac{z-\bar{z}}{2i}\)
Solution:
let z = x + iy
\(\overline {z}\) = x – iy

Hence proved

Question 6.
Find the least value of the positive integer n for which (√3 + i)ⁿ (i) real, (ii) purely imaginary.
Solution:
Given (√3 + i)ⁿ
= (√3)² + 2i √3 + (i)²
= 3 + 2i √3 – 1
= 2 + 2i √3
= 2(1 + i√3)
put n = 3 or 4 or 5
then real part is not possible

which is purely real ∴ n = 6

(ii) (√3 + i)ⁿ

which is purely imaginary
∴ n = 3

Question 7.
Show that
(i) (2 + i√3)¹⁰ – (2 – i√3)¹⁰ is purely imaginary.
Solution:
Let z = (2 + i√3)¹⁰ – (2 – i√3)¹⁰
Let Z

= (2 – i√3)¹⁰ – (2 + i√3)¹⁰
= -[(z + i√3)¹⁰ – (2 – i√3)¹⁰]
= -z
(2 + i√3)¹⁰ – (2 – i√3)¹⁰ is purely imaginary

(ii) \(\left(\frac{19-7 i}{9+i}\right)^{12}\) + \(\left(\frac{20-5 i}{7-6 i}\right)^{12}\) is real
Solution:

∴ z is real.

Students can download 6th Science Term 3 Chapter 6 Hardware and Software Questions and Answers, Notes, Samacheer Kalvi 6th Science Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Science Solutions Term 3 Chapter 6 Hardware and Software

Samacheer Kalvi 6th Science Hardware and Software Text Book Back Questions and Answers

I. Choose the correct Answer:

Question 1.
Find out the part that is not found in the CPU?
a. MotherBoard
b. SMPS
c. RAM
d. Mouse
Answer:
d. Mouse

Question 2.
Which of the following is correct?
(a) Free and Open source
(b) Free and Traditional software
(c) passive and Open source
(d) Passive and Traditional source
Answer:
(a) Free and Open source

Question 3.
LINUX is a
a. Paid Software
b. Licensed Software
c. Free and Proprietary software
d. Free and Open-source software
Answer:
d. Free and Open-source software

Question 4.
Find out Paid and Proprietary software from the given list
(a) Windows
(b) MAC OS
(c) Adobe Photoshop
(d) All the above
Answer:
(d) All the above

Question 5.
……….. is an Operating System
a. Android
b. Chrome
c. Internet
d. Pendrive
Answer:
a. Android

II. Match the following

Answer:
1. – b
2. – e
3. – d
4. – c
5. – a

III. Short answer:

Question 1.
What are Hardware and Software?
Answer:
Hardware:

1. Hardware is the parts of the computer which we can touch and feel.
2. Hardware includes input and output devices, Cabinet, Hard disk, Mother Board, SMPS, CPU, RAM, CD Drive, and Graphics card.

Software :

1. Software is programmed and coded application to process the input information.
2. The software processes the data by converting the input information into coding or programmed language.
3. Touching and feeling is not possible. But, we can see the functions of the software in the form of output.

Question 2.
What do you mean by Operating System? How does it work?
Answer:

1. System software (operating system is software that makes the hardware devices process the data inputted by the user and to display the result on the output devices like a monitor. Without the operating system, the computer cannot function on its own. Popular OS are Linux, Windows, Mac, Android, etc.

Question 3.
What is Free and Open Source Software? Give any two examples?
Answer:

1. Free and open software is available free of cost and can be shared with many end-users.
2. Free software is editable and customizable by the user and this leads to the update or development of new software.
3. Examples: 1. Linux, 2. Geogebra.

Samacheer Kalvi 6th Science Hardware and Software Additional Important Questions and Answers

I. Choose the right answer:

Question 1.
Email existed before the
(a) Google
(b) Chrome
(c) World Wide Web
(d) Whatsapp
Answer:
(c) World Wide Web

Question 2.
A _____ device helps to enter input information.
(a) Hardware
(b) Software
(c) Monitor
(d) Modem
Answer:
(a) Hardware

Question 3.
Completes one or more than two works of the end-user?
(a) System software
(b) Operating system
(c) Free software
(d) Application software
Answer:
(d) Application software

Question 4.
The _____ can be installed in the hard disk for the usage on a particular computer.
(a) Opening system
(b) Translator
(c) Application program
(d) Image editor
Answer:
(c) Application Program

Question 5.
___________ is an operating system
(a) Linux
(b) Chrome
(c) Google
(d) Pen drive
Answer:
(a) Linux

II. Match the following:

Answer:
1. – c
2. – d
3. – a
4. – e
5. – b

III. Short Answer:

Question 1.
What are the types of software?
Answer:
Software is divided into two types based on the process. They are:

1. System Software (Operating System).
2. Application software.

Question 2.
What is Application software?
Answer:
It is a program or a group of programs designed for the benefit of end-user to work on computers. The application programs can be installed in the hard disk for the usage on a particular computer. This type of application program completes one or more than two works of the end-user.

Question 3.
Give some examples of Application Software.
Answer:
The following are the examples of the application program: Video player, Audio player, Word processing software, Drawing tools, Editing software, etc.