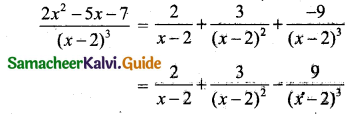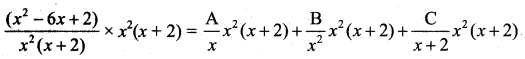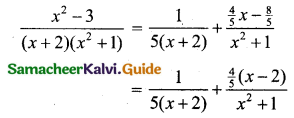Students can download 11th Business Maths Chapter 2 Algebra Ex 2.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 2 Algebra Ex 2.3
Samacheer Kalvi 11th Business Maths Algebra Ex 2.3 Text Book Back Questions and Answers
Question 1.
If nP4 = 12(nP2), find n.
Solution:
Given that nP4 = 12(nP2)
n(n – 1) (n – 2) (n – 3) = 12n(n – 1)
Cancelling n(n – 1) on both sides we get
(n – 2) (n – 3) = 4 × 3
We have product of consecutive number on both sides with decreasing order.
n – 2 = 4
∴ n = 6
![]()
Question 2.
In how many ways 5 boys and 3 girls can be seated in a row so that no two girls are together?
Solution:
5 boys can be seated among themselves in 5P5 = 5! Ways. After this arrangement, we have to arrange the three girls in such a way that in between two girls there atleast one boy. So the possible places girls can be placed with the × symbol given below.
× B × B × B × B × B ×
∴ There are 6 places to seated by 3 girls which can be done 6P3 ways.
∴ Total number of ways = 5! × 6P3
= 120 × (6 × 5 × 4)
= 120 × 120
= 14400
Question 3.
How many 6-digit telephone numbers can be constructed with the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 if each number starts with 35 and no digit appears more than once?
Solution:
Given that each number starts with 35. We need a 6 digit number. So we have to fill only one’s place, 10’s place, 100th place, and 1000th places. We have to use 10 digits.
In these digits, 3 and 5 should not be used as a repetition of digits is not allowed. Except for these two digits, we have to use 8 digits. One’s place can be filled by any of the 8 digits in different ways, 10’s place can be filled by the remaining 7 digits in 7 different ways.
100th place can be filled by the remaining 6 different ways and 1000th place can be filled by the remaining 5 digits in 5 different ways.
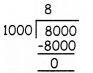
∴ Number of 6 digit telephone numbers = 8 × 7 × 6 × 5 = 1680
![]()
Question 4.
Find the number of arrangements that can be made out of the letters of the word “ASSASSINATION”.
Solution:
The number of letters of the word “ASSASSINATION” is 13.
The letter A occurs 3 times
The letter S occurs 4 times
The letter I occur 2 times
The letter N occurs 2 times
The letter T occurs 1 time
The letter O occurs 1 time
∴ Number of arrangements = \(\frac{13 !}{3 ! 4 ! 2 ! 2 ! 1 ! 1 !}=\frac{13 !}{3 ! 4 ! 2 ! 2 !}\)
Question 5.
(a) In how many ways can 8 identical beads be strung on a necklace?
(b) In how many ways can 8 boys form a ring?
Solution:
(a) Number of ways 8 identical beads can be stringed by \(\frac{(8-1) !}{2}=\frac{7 !}{2}\)
(b) Number of ways 8 boys form a ring = (8 – 1)! = 7!
![]()
Question 6.
Find the rank of the word ‘CHAT’ in the dictionary.
Solution:
The letters of the word CHAT in alphabetical order are A, C, H, T. To arrive the word CHAT, first, we have to go through the word that begins with A. If A is fixed as the first letter remaining three letters C, H, T can be arranged among themselves in 3! ways. Next, we select C as the first letter and start arranging the remaining letters in alphabetical order. Now C and A is fixed remaining two letters can be arranged in 2! ways. Next, we move on H with C, A, and H is fixed the letter T can be arranged in 1! ways.
∴ Rank of the word CHAT = 3! + 2! + 1! = 6 + 2 + 1 = 9
Note: The rank of a given word is basically finding out the position of the word when possible words have been formed using all the letters of the given word exactly once and arranged in alphabetical order as in the case of dictionary. The possible arrangement of the word CHAT are (i) ACHT, (ii) ACTH, (iii) AHCT, (iv) AHTC, (v) ATCH, (vi) ATHC, (vii) CAHT, (viii) CATH, (ix) CHAT. So the rank of the word occurs in the ninth position.
∴ The rank of the word CHAT is 9.