Category: Class 11

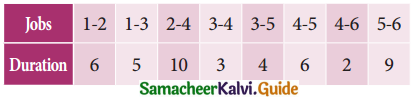
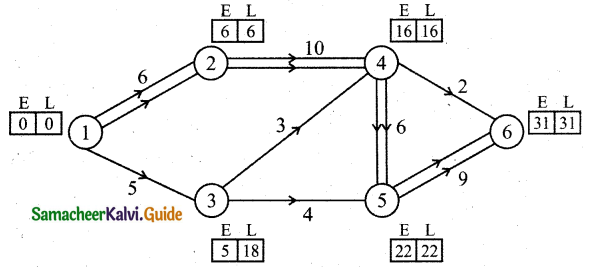
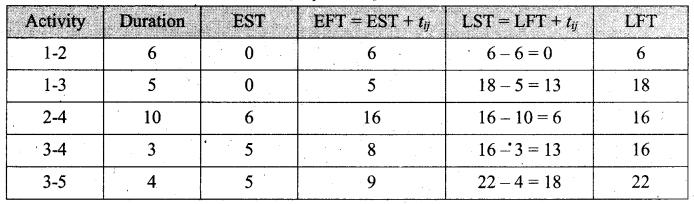
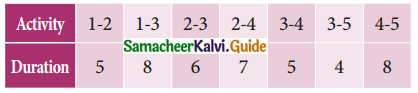
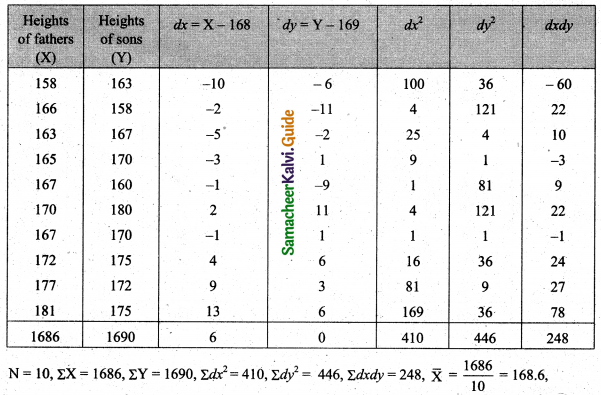
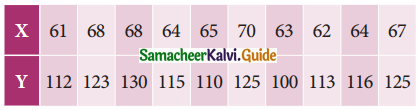
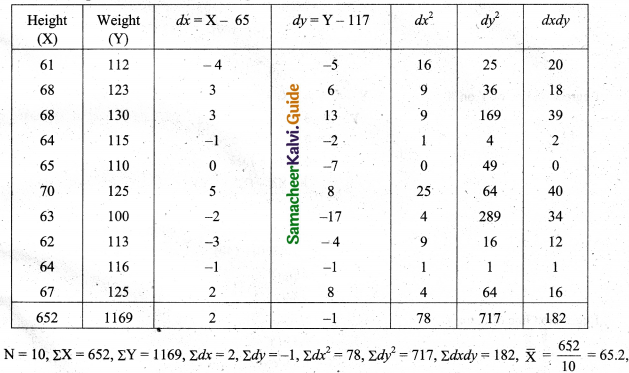
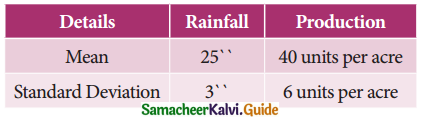
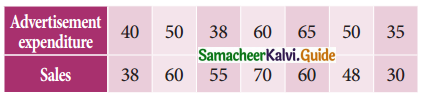
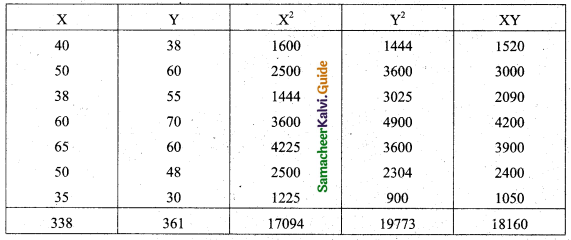
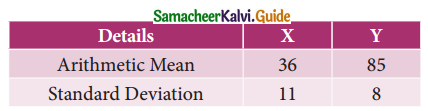
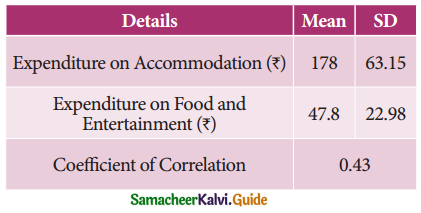
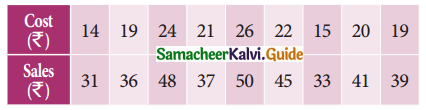
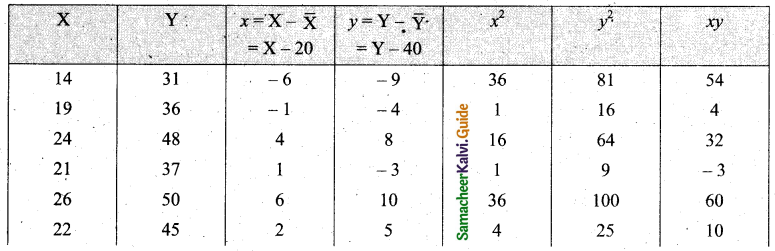
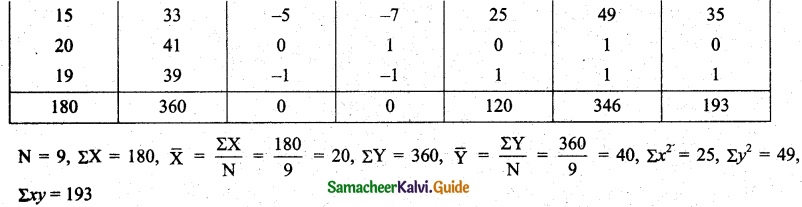
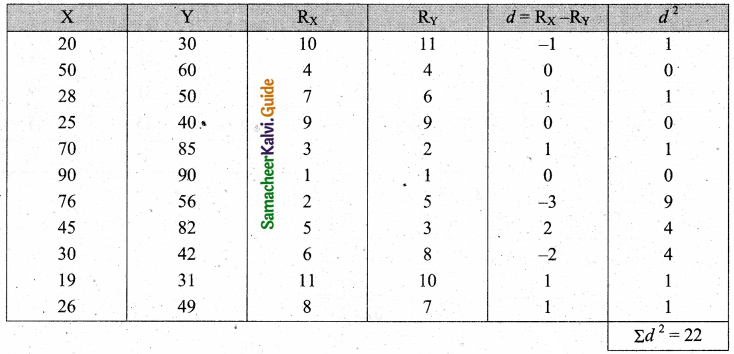
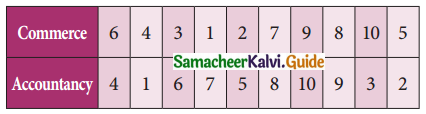
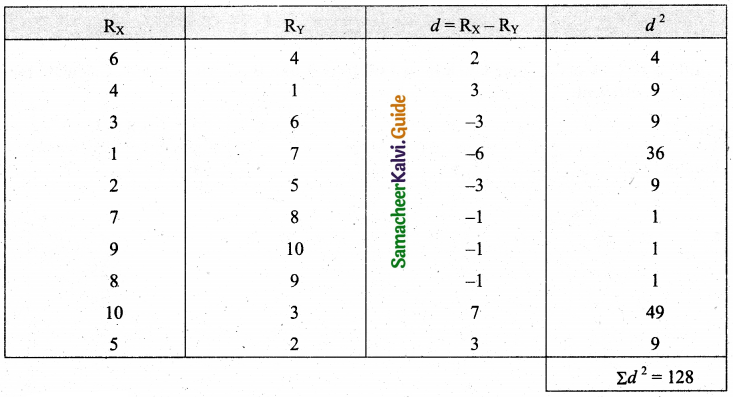
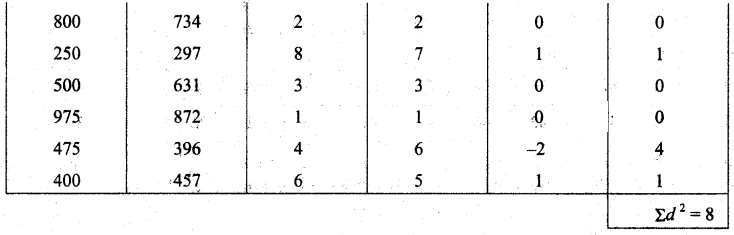
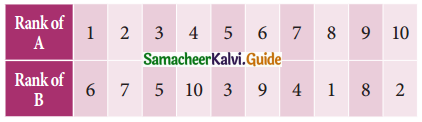
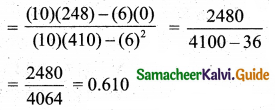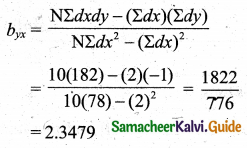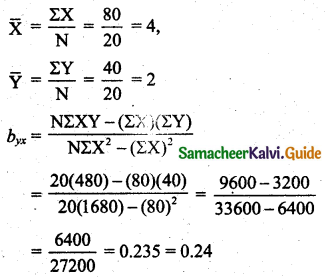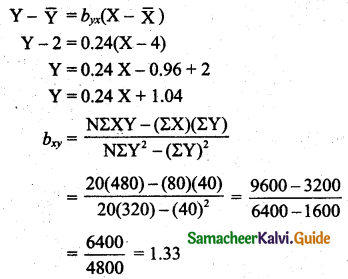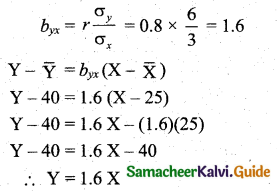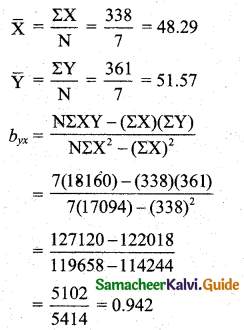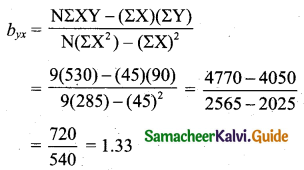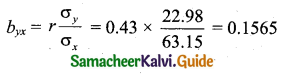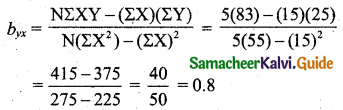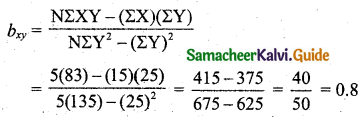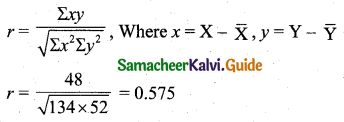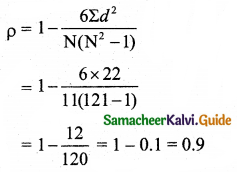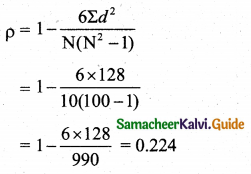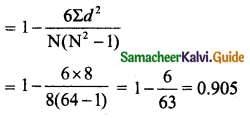Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.1

Question 1.
Write the following in roaster form.
(i) {x ∈ N : x² < 121 and x is a prime}
Answer:
Let A = { x ∈ N : x² < 121 and x is a prime }
A = { 2, 3, 5, 7 }

(ii) The set of positive roots of the equation (x – 1) ( x + 1) (x – 1 ) = 0
Answer:
The set of positive roots of the equations
(x – 1) (x + 1) (x² – 1) = 0
(x – 1 ) (x + 1 ) (x + 1) (x – 1) = 0
(x + 1 )² (x – 1)² = 0
(x + 1)² = 0 or (x – 1)² = 0
x + 1 = 0 or x – 1 = 0
x = -1 or x = 1
A = { 1 }

(iii) {x ∈ N : 4x + 9 < 52}
Answer:
4x + 9 < 52
4x + 9 – 9 < 52 – 9
4x < 43
x < \(\frac{43}{4}\) (i.e.) x < 10.75 4
But x ∈ N
∴ A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

(iv)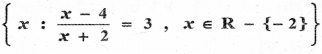
Answer:
Let A =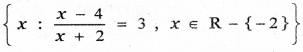
⇒ \(\frac{x-4}{x+2}\) = 3
⇒ x – 4 = 3(x + 2)
⇒ x – 4 = 3x + 6
⇒ 3x – x = – 4 – 6
2x = – 10
⇒ x = \(-\frac{10}{2}\) = -5
A = { -5 }

Question 2.
Write the set {-1, 1} in set builder form.
Answer:
A = {x : x² – 1 = 0, x ∈ R}

Question 3.
State whether the following sets are finite or infinite.
(i) {x ∈ N : x is an even prime number }
Answer:
Let A = { x ∈ N : x is an even prime number )
A = {2}
A is a finite set.

(ii) {x ∈ N: x is an odd prime number }
Answer:
Let B = {x ∈ N : x is an odd prime number}
B = {1, 3, 5, 7, 11, …………….. }
B is an infinite set.

(iii) {x ∈ Z : x is even and < 10 }
Answer:
C = {x ∈ Z : x is even and< 10}
C = { ……….. -8, -6, -4, -2, 0, 2, 4, 6, 8}
C is an infinite set.

(iv) {x ∈ R : x is a rational number }
Answer:
D = { x ∈ R : x is a rational number }
D is an infinite set.

(v) {x ∈ N: x is a rational number }
Answer:
E = { x ∈ N : x is a rational number )
E = {1, 2, 3, 4, 5, 6, …………..)
Every integer is a rational number.
∴ E is an infinite set.

Question 4.
By taking suitable sets A, B, C, verify the following results.
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
Answer:
To prove: A × (B ∩ C) = (A × B) ∩ (A × C)
B ∩ C = {8}; A = {1, 2, 5, 7}
So A × (B ∩ C) = {1, 2, 5, 7} × {8}
= {(1, 8), (2. 8), (5, 8), (7, 8)}
Now A x B = {(1, 2), (1, 7), (1, 8), (1, 9), (2, 2), (2, 7), (2, 8), (2, 9), (5, 2), (5, 7), (5, 8), (5, 9), (7, 2), (7, 7), (7, 8), (7, 9)} …. ( 1)
A × C = {(1, 1), (1, 5),(1, 8), (1, 10), (2, 1), (2, 5), (2, 8), (2, 10), (5, 1), (5, 5), (5, 8), (5, 10), (7, 1), (7, 5), (7, 8), (7, 10)}
(A × B) ∩ (A × C) = {(1, 8), (2, 8), (5, 8), (7, 8)} ……… (2)
(1) = (2)
⇒ A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) A × (B ∪ C) = (A × B) ∪ (A × C)
Answer:
Let A = {1, 2} , B = {3, 4}, C = {4, 5}
B ∪ C = {3, 4} ∪ {4, 5}
B ∪ C = {3, 4, 5)
A × (B ∪ C) = {1, 2} × {3, 4, 5}
A × (B ∪ C) = { (1, 3),( 1, 4),(1, 5),(2, 3), (2, 4),(2,5)} ——– (1)
A × B = {1, 2} × {3, 4}
A × B = { (1, 3), (1, 4), (2, 3), (2, 4) }
A × C = {1, 2} × {4, 5}
A × C = { (1, 4), (1, 5), (2, 4), (2, 5 )}
(A × B) ∪ (A × C) = {(1, 3), (1, 4), (2, 3), (2, 4)} ∪ {(1, 4 ), (1, 5 ), ( 2, 4 ), (2, 5)}
(A × B) ∪ (A × C) = { (1, 3) (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)} —— (2)
From equations (1) and (2)
A × (B U C) = (A × B) U (A × C)

(iii) (A × B) ∩ (B × A) = (A ∩ B) × ( B ∩ A)
Answer:
A × B = {(1, 2), (1, 7), (1, 8), (1, 9) (2, 2), (2, 7), (2, 8), (2, 9) (5, 2), (5, 7), (5, 8), (5, 9) (7, 2), (7, 7), (7, 8), (7, 9)}
B × A = {(2, 1), (2, 2), (2, 5), (2, 7) (7, 1), (7, 2), (7, 5), (7, 7) (8, 1), (8, 2), (8, 5), (8, 7) (9,1), (9, 2), (9, 5), (9, 7)}
L.H.S. (A × B) ∩ (B × A) = {(2, 2), (2, 7), (7, 2), (7, 7)} …. (1)
R.H.S. A ∩ B = {2, 7}
B ∩ A = {2, 7}
(A ∩ B) × (B ∩ A) = {2, 7} × {2, 7}
= {(2, 2), (2, 7), (7, 2), (7, 7)} ……… (2)
(1) = (2) ⇒ LHS = RHS

(iv) C – (B – A) = (C ∩ A) ∪ (C ∩ B’)
Answer:
Let A = {1, 2, 3) , B = {2, 3, 4) , C = {3, 4, 5}

B – A = { 2, 3, 4 ) – {1, 2, 3}
B – A = {4}
C – (B – A) = {3, 4, 5} – {4}
C – (B – A) = {3, 5} —- (1)
C ∩ A = {3, 4, 5} ∩ { 1, 2, 3)
C ∩ A = {3}
B’ = {1, 5}
C ∩ B’ = {3, 4, 5} ∩ {1, 5}
C ∩ B’ = {5}
(C ∩ A) ∪ (C∩B’) = {3} ∪ {5}
(C∩A) ∪ (C ∩ B’) = {3, 5} —— (2)
From equations (1) and (2)
C – (B – A) = (C ∩ A) u (C ∩ B’)

(v) (B – A) ∩ C = (B ∩ C) – A = B ∩ (C – A)
Answer:
To prove (B – A) ∩ C = (B ∩ C) – A = B ∩ (C – A)
A= {1, 2, 5, 7}, B = {2, 7, 8, 9}, C = {1, 5, 8, 10}
Now B – A = {8, 9}
(B – A) ∩ C = {8} ……. (1)
B ∩ C = {8}
A = {1, 2, 5, 7}
So (B ∩ C) – A = {8} …… (2)
C – A = {8, 10}
B = {2, 7, 8, 9}
B ∩ (C – A) = {8} …. (3)
(1) = (2) = (3)

(vi) (B – A) ∪ C = (B ∪ C) – (A – C)
Answer:
Let A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8}
B – A = {3, 4, 5, 6} – {1, 2, 3, 4}
B – A = {5, 6}
(B – A) ∪ C = {5, 6} ∪ {5, 6, 7, 8}
(B – A) ∪ C = { 5 , 6 , 7 , 8 } ——- (1)
B ∪ C = { 3, 4, 5, 6 } ∪ { 5, 6, 7,8 }
B ∪ C = { 3, 4, 5, 6, 7, 8 }
A – C = { 1, 2, 3, 4 } – { 5, 6, 7, 8 }
A – C = { 1 , 2, 3 , 4 }
(B ∪ C) – (A – C) = {3, 4, 5, 6, 7, 8} – {1, 2, 3, 4}
(B ∪ C) – (A – C) = { 5, 6, 7, 8 } —-(2)
From equations (1) and (2)
(B – A) ∪ C = (B ∪ C) – (A – C)

Question 5.
Justify the trueness of the statement: “An element of a set can never be a subset of itself”.
Answer:
A set itself can be a subset of itself (i.e.) A ⊆ A.
But it cannot be a proper subset.

Question 6.
If n(P(A)) = 1024, n(A ∪ B) = 15 and n(P(B)) = 32, find n(A ∩ B).
Answer:
Given n(P(A)) = 1024 , n(A ∪ B) = 15, n(P(B)) = 32
n(P(A)) = 1024 = 2¹⁰ n(A) = 10
n(P(B)) = 32 = 2⁵ = n(B) = 5
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
15 = 10 + 5 – n(A ∩ B)
15 = 15 – n (A ∩ B)
n(A ∩ B) = 0

Question 7.
If n (A ∩ B ) = 3 and n(A ∪ B ) = 10 , then find n(P(A ∆ B)).
Answer:

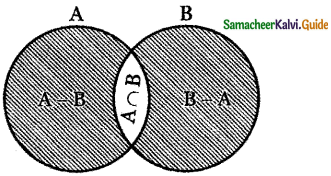
n(A ∪ B) = 10; n(A ∩ B) = 3
n(A ∆ B) = 10 – 3 = 7
and n(P(A ∆ B)) = 27 = 128

Question 8.
For a set A, A × A contains 16 elements and two of its elements are (1, 3) and (0, 2). Find the elements of A.
Answer:
Given A × A contains 16 elements.
∴ A contains 4 elements.
Also, (1, 3) and (0, 2) are two elements of A × A.
∴ A = { 0, 1, 2, 3 }

Question 9.
Let A and B be two sets such that n (A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B , find A and B, where x , y , z are distinct elements.
Answer:
n(A) = 3 ⇒ set A contains 3 elements
n(B) = 2 ⇒ set B contains 2 elements –
we are given (x, 1), (y, 2), (z, 1) are elements in A × B ⇒ A = {x, y, z} and B = {1, 2}

Question 10.
If A × A has 16 elements, S = { ( a, b ) ∈ A × A: a < b } ; (-1, 2) and (0, 1) are two elements of S , then find the remaining elements of S.
Answer:
Given A × A has 16 elements.
∴ A has 4 elements.
Also S = {(a, b) ∈ A × A; a < b}
Given (-1, 2) and (0, 1) ∈ S
A = {-1, 0 , 1 , 2 }
The elements of S are
S = { (-1, 0), (-1, 1) ,(-1, 2),(0, 1), (0, 2), (1, 2)}
∴ The other elements of the sets are
(-1, 0), (-1, 1) , (0, 2), (1, 2)

Subject Matter Experts at SamacheerKalvi.Guide have created Tamilnadu State Board 11th Maths Solutions Book Pdf Free Download New Syllabus of Volume 1 and Volume 2 in English Medium and Tamil Medium are part of Samacheer Kalvi 11th Books Solutions.

Let us look at these TN Board Samacheer Kalvi 11th Std Maths Guide Pdf Free Download of Text Book Back Questions and Answers, Notes, Chapter Wise Important Questions, Model Question Papers with Answers, Study Material, Question Bank, Formulas and revise our understanding of the subject.

Students can also read Tamil Nadu 11th Maths Model Question Papers 2020-2021 English & Tamil Medium.

Tamilnadu State Board 11th Maths Solutions Book Pdf Free Download New Syllabus

11th Maths Book Back Answers Solutions Guide

You can download Tamilnadu State Board Class 11th Maths Book Volume 1 Solutions Answers Guide Pdf and 11th Maths Book Volume 2 Answers Solutions Guide Pdf.

11th Maths Book Volume 1 Solutions Answers Guide Pdf

Tamilnadu State Board 11th Maths Solutions Book Pdf Free Download Chapter 1 Sets, Relations and Functions

• Chapter 1 Sets, Relations and Functions Ex 1.1
• Chapter 1 Sets, Relations and Functions Ex 1.2
• Chapter 1 Sets, Relations and Functions Ex 1.3
• Chapter 1 Sets, Relations and Functions Ex 1.4
• Chapter 1 Sets, Relations and Functions Ex 1.5

11th Maths Book Volume 1 Solutions Answers Guide Pdf Chapter 2 Basic Algebra

• Chapter 2 Basic Algebra Ex 2.1
• Chapter 2 Basic Algebra Ex 2.2
• Chapter 2 Basic Algebra Ex 2.3
• Chapter 2 Basic Algebra Ex 2.4
• Chapter 2 Basic Algebra Ex 2.5
• Chapter 2 Basic Algebra Ex 2.6
• Chapter 2 Basic Algebra Ex 2.7
• Chapter 2 Basic Algebra Ex 2.8
• Chapter 2 Basic Algebra Ex 2.9
• Chapter 2 Basic Algebra Ex 2.10
• Chapter 2 Basic Algebra Ex 2.11
• Chapter 2 Basic Algebra Ex 2.12
• Chapter 2 Basic Algebra Ex 2.13

11th Standard Maths Guide Pdf Free Download Chapter 3 Trigonometry

• Chapter 3 Trigonometry Ex 3.1
• Chapter 3 Trigonometry Ex 3.2
• Chapter 3 Trigonometry Ex 3.3
• Chapter 3 Trigonometry Ex 3.4
• Chapter 3 Trigonometry Ex 3.5
• Chapter 3 Trigonometry Ex 3.6
• Chapter 3 Trigonometry Ex 3.7
• Chapter 3 Trigonometry Ex 3.8
• Chapter 3 Trigonometry Ex 3.9
• Chapter 3 Trigonometry Ex 3.10
• Chapter 3 Trigonometry Ex 3.11
• Chapter 3 Trigonometry Ex 3.12

TN 11th Maths Guide Pdf Free Download for 11th Samacheer Kalvi Chapter 4 Combinatorics and Mathematical Induction

• Chapter 4 Combinatorics and Mathematical Induction Ex 4.1
• Chapter 4 Combinatorics and Mathematical Induction Ex 4.2
• Chapter 4 Combinatorics and Mathematical Induction Ex 4.3
• Chapter 4 Combinatorics and Mathematical Induction Ex 4.4
• Chapter 4 Combinatorics and Mathematical Induction Ex 4.5

11th Standard State Board Maths Guide Pdf Free Download Chapter 5 Binomial Theorem, Sequences and Series

• Chapter 5 Binomial Theorem, Sequences and Series Ex 5.1
• Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2
• Chapter 5 Binomial Theorem, Sequences and Series Ex 5.3
• Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4
• Chapter 5 Binomial Theorem, Sequences and Series Ex 5.5

11th Std Samacheer Kalvi Maths Guide Free Download Chapter 6 Two Dimensional Analytical Geometry

• Chapter 6 Two Dimensional Analytical Geometry Ex 6.1
• Chapter 6 Two Dimensional Analytical Geometry Ex 6.2
• Chapter 6 Two Dimensional Analytical Geometry Ex 6.3
• Chapter 6 Two Dimensional Analytical Geometry Ex 6.4
• Chapter 6 Two Dimensional Analytical Geometry Ex 6.5

11th Maths Book Volume 2 Answers Solutions Guide Pdf

11th Maths Book Volume 2 Answers Solutions Guide Pdf Chapter 7 Matrices and Determinants

• Chapter 7 Matrices and Determinants Ex 7.1
• Chapter 7 Matrices and Determinants Ex 7.2
• Chapter 7 Matrices and Determinants Ex 7.3
• Chapter 7 Matrices and Determinants Ex 7.4
• Chapter 7 Matrices and Determinants Ex 7.5

11th Std State Board Maths Solution Book Pdf Chapter 8 Vector Algebra – I

• Chapter 8 Vector Algebra – I Ex 8.1
• Chapter 8 Vector Algebra – I Ex 8.2
• Chapter 8 Vector Algebra – I Ex 8.3
• Chapter 8 Vector Algebra – I Ex 8.4
• Chapter 8 Vector Algebra – I Ex 8.5

Tn 11th Maths Solution Book Free Download Chapter 9 Differential Calculus – Limits and Continuity

• Chapter 9 Limits and Continuity Ex 9.1
• Chapter 9 Limits and Continuity Ex 9.2
• Chapter 9 Limits and Continuity Ex 9.3
• Chapter 9 Limits and Continuity Ex 9.4
• Chapter 9 Limits and Continuity Ex 9.5
• Chapter 9 Limits and Continuity Ex 9.6

11th Std Maths Book Solutions Samacheer Kalvi Chapter 10 Differential Calculus – Differentiability and Methods of Differentiation

• Chapter 10 Differentiability and Methods of Differentiation Ex 10.1
• Chapter 10 Differentiability and Methods of Differentiation Ex 10.2
• Chapter 10 Differentiability and Methods of Differentiation Ex 10.3
• Chapter 10 Differentiability and Methods of Differentiation Ex 10.4
• Chapter 10 Differentiability and Methods of Differentiation Ex 10.5

Samacheer Kalvi 11th Maths Important Questions Chapter 11 Integral Calculus

• Chapter 11 Integral Calculus Ex 11.1
• Chapter 11 Integral Calculus Ex 11.2
• Chapter 11 Integral Calculus Ex 11.3
• Chapter 11 Integral Calculus Ex 11.4
• Chapter 11 Integral Calculus Ex 11.5
• Chapter 11 Integral Calculus Ex 11.6
• Chapter 11 Integral Calculus Ex 11.7
• Chapter 11 Integral Calculus Ex 11.8
• Chapter 11 Integral Calculus Ex 11.9
• Chapter 11 Integral Calculus Ex 11.10
• Chapter 11 Integral Calculus Ex 11.11
• Chapter 11 Integral Calculus Ex 11.12
• Chapter 11 Integral Calculus Ex 11.13

Samacheer Kalvi Class 11th Maths Book Solutions Chapter 12 Introduction to Probability Theory

• Chapter 12 Introduction to Probability Theory Ex 12.1
• Chapter 12 Introduction to Probability Theory Ex 12.2
• Chapter 12 Introduction to Probability Theory Ex 12.3
• Chapter 12 Introduction to Probability Theory Ex 12.4
• Chapter 12 Introduction to Probability Theory Ex 12.5

We hope these Tamilnadu State Board Class 11th Maths Solutions Book Volume 1 and Volume 2 Pdf Free Download New Syllabus in English Medium and Tamil Medium will help you get through your subjective questions in the exam.

Let us know if you have any concerns regarding TN Board 11th Standard Samacheer Kalvi Maths Guide Pdf Free Download of Text Book Back Questions and Answers, Notes, Chapter Wise Important Questions, Model Question Papers with Answers, Study Material, Question Bank, Formulas, drop a comment below and we will get back to you as soon as possible.

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 10 Operations Research Ex 10.3

Samacheer Kalvi 11th Business Maths Operations Research Ex 10.3 Text Book Back Questions and Answers

Choose the correct answer.

Question 1.
The critical path of the following network is:

(a) 1-2-4-5
(b) 1-3-5
(c) 1-2-3-5
(d) 1-2-3-4-5
Answer:
(d) 1-2-3-4-5
Hint:
1-2-4-5 ⇒ EFT = 20 + 12 + 10 = 42
1-3-5 ⇒ EFT = 25 + 8 = 33
1-2-3-5 ⇒ EFT = 20 + 10 + 8 = 38
1-2-3-4-5 ⇒ EFT = 20 + 10 + 5 + 10 = 45

Question 2.
Maximize: z = 3x₁ + 4x₂ subject to 2x₁ + x₂ ≤ 40, 2x₁ + 5x₂ ≤ 180, x₁, x₂ ≥ 0. In the LPP, which one of the following is feasible comer point?
(a) x₁ = 18, x₂ = 24
(b) x₁ = 15, x₂ = 30
(c) x₁ = 2.5, x₂ = 35
(d) x₁ = 20.5, x₂ = 19
Answer:
(c) x₁ = 2.5, x₂ = 35
Hint:
z = 3x₁ + 4x₂
Let us solve the equations
2x₁ + x₂ = 40 ………(1)
2x₁ + 5x₂ = 180 ……….(2)
(1) – (2) ⇒ -4x₂ = -140
x₂ = 35
We have 2x₁ + x₂ =40
2x₁ + 35 = 40
2x₁ = 5
x₁ = 2.5

Question 3.
One of the conditions for the activity (i, j) to lie on the critical path is:
(a) E_j – E_i = L_j – L_i = t_ij
(b) E_i – E_j = L_j – L_i = t_ij
(c) E_j – E_i = L_i – L_j = t_ij
(d) E_j – E_i = L_j – L_i ≠ t_ij
Answer:
(a) E_j – E_i = L_j – L_i = t_ij

Question 4.
In constructing the network which one of the following statement is false?
(a) Each activity is represented by one and only one arrow, (i.e) only one activity can connect any two nodes.
(b) Two activities can be identified by the same head and tail events.
(c) Nodes are numbered to identify an activity uniquely. Tail node (starting point) should be lower than the head node (end point) of an activity.
(d) Arrows should not cross each other.
Answer:
(b) Two activities can be identified by the same head and tail events.

Question 5.
In a network while numbering the events which one of the following statement is false?
(a) Event numbers should be unique.
(b) Event numbering should be carried out on a sequential basis from left to right.
(c) The initial event is numbered 0 or 1.
(d) The head of an arrow should always bear a number lesser than the one assigned at the tail of the arrow.
Answer:
(d) The head of an arrow should always bear a number lesser than the one assigned at the tail of the arrow.

Question 6.
A solution which maximizes or minimizes the given LPP is called:
(a) a solution
(b) a feasible solution
(c) an optimal solution
(d) none of these
Answer:
(a) a solution

Question 7.
In the given graph the coordinates of M₁ are

(a) x₁ = 5, x₂ = 30
(b) x₁ = 20, x₂ = 16
(c) x₁ = 10, x₂ = 20
(d) x₁ = 20, x₂ = 30
Answer:
(c) x₁ = 10, x₂ = 20
Hint:
4x₁ + 2x₂ = 80 (or) 2x₁ + x₂ = 40
2x₁ + x₂ = 40 ……(1)
2x₁ + 5x₂ = 120 ……(2)
(1) – (2) ⇒ -4x₂ = -80
x₂ = 20
But, 2x₁ + x₂ = 40
2x₁ + 20 = 20
x₁ = 10

Question 8.
The maximum value of the objective function Z = 3x + 5y subject to the constraints x > 0, y > 0 and 2x + 5y ≤ 10 is:
(a) 6
(b) 15
(c) 25
(d) 31
Answer:
(b) 15
Hint:
Let 2x + 5y = 10


∴ Maximum Value = 15

Question 9.
The minimum value of the objective function Z = x + 3y subject to the constraints 2x + y ≤ 20, x + 2y ≤ 20, x > 0 and y > 0 is:
(a) 10
(b) 20
(c) 0
(d) 5
Answer:
(c) 0
Hint:
O(0, 0) is a comer point.
So Z = 0 + 3(0) = 0
∴ Minimum value is 0

Question 10.
Which of the following is not correct?
(a) Objective that we aim to maximize or minimize
(b) Constraints that we need to specify
(c) Decision variables that we need to determine
(d) Decision variables are to be unrestricted
Answer:
(d) Decision variables are to be unrestricted

Question 11.
In the context of network, which of the following is not correct?
(a) A network is a graphical representation.
(b) A project network cannot have multiple initial and final nodes
(c) An arrow diagram is essentially a closed network
(d) An arrow representing an activity may not have a length and shape
Answer:
(d) An arrow representing an activity may not have a length and shape

Question 12.
The objective of network analysis is to:
(a) Minimize total project cost
(b) Minimize total project duration
(c) Minimize production delays, interruption and conflicts
(d) All the above
Answer:
(b) Minimize total project duration

Question 13.
Network problems have advantage in terms of project:
(a) Scheduling
(b) Planning
(c) Controlling
(d) All the above
Answer:
(d) All the above

Question 14.
In critical path analysis, the word CPM mean:
(a) Critical path method
(b) Crash projecf management
(c) Critical project management
(d) Critical path management
Answer:
(a) Critical path method

Question 15.
Given an L.P.P maximize Z = 2x₁ + 3x₂ subject to the constrains x₁ + x₂ ≤ 1, 5x₁ + 5x₂ ≥ 0 and x₁ ≥ 0, x₂ ≥ 0 using graphical method, we observe:
(a) No feasible solution
(b) unique optimum solution
(c) multiple optimum solution
(d) none of these
Answer:
(a) No feasible solution

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 10 Operations Research Ex 10.2

Samacheer Kalvi 11th Business Maths Operations Research Ex 10.2 Text Book Back Questions and Answers

Question 1.
Draw the network for the project whose activities with their relationships are given below:
Activities A, D, E can start simultaneously; B, C > A; G, F > D, C; H > E, F.
Solution:
Given: (i) A, D, E can start simultaneously.
(iii) A < B, C; C, D < G, F; E, F < H
Working rule:
A < B, C implies activity A is the immediate predecessor of activities B and C.
i.e., for activities B and C to occur, activity ‘A’ has to be completed.
Similarly for activities G, F to occur D and C has to completed for activity H to occur E and F has to be completed.
Step-1:

(∵ A, D and E are independents events)
Step-2:

Note: Activities B, G and H are not a part of any activities immediate predecessor. So they have to merge into the lost node 5.

Question 2.
Draw the event oriented network for the following data:

Solution:
Step-1:

Step-2:

Step-3:

Question 3.
Construct the network for the projects consisting of various activities and their precedence relationships are as given below:
A, B, C can start simultaneously: A < F, E; B < D, C; E, D < G
Solution:
Step-1:

Step-2:

Step-3:

Question 4.
Construct the network for each the projects consisting of various activities and their precedence relationships are as given below:

Solution:
Step-1:

Step-2:

Step-3:

Question 5.
Construct the network for the project whose activities are given below.

Calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity. Determine the critical path and the project completion time.
Solution:

Forward pass:
E₁ = 0 + 3 = 3
E₂ = E₁ + t₁₂ = 8 + 3 = 11
E₃ = 3 + 12 = 15
E₄ = E₂ + 6 (or) E₃ + 3 = 11 + 6 (or) 15 + 3 = 18
[We must select a maximum value for forwarding pass]
E₄ = 15 + 3 = 18
E₂ = E₂ + 3 = 11 + 3 = 14
E₆ = E₃ + 8 = 15 + 8 = 23
E₇ = E₆ + 8 = 23 + 8 = 31
Backward pass:
L₇ = 31
L₆ = L₇ – 8 = 31 – 8 = 23
L₅ = L₇ – 3 = 31 – 3 = 28
L₄ = L₇ – 5 = 31 – 5 = 26
L₃ = L₆ – 8 = 23 – 8 = 15
L₂ = L₅ – 3 (or) L₄ – 6 = (28 – 3) (or) (26 – 6) = 25 (or) 20
[We must select a minimum value for a backward pass and maximum value for forwarding pass]
L₁ = L₂ – 8 (or) L₃ – 12 = 20 – 8 (or) 15 – 12 = 12 (or) 3 = 3
L₀ = 0

Critical path 0-1-3-6-7 and the duration is 31 works.

Question 6.
A project schedule has the following characteristics:

Construct the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
Solution:

Forward pass:
E₁ = 0
E₂ = 0 + 4 = 4
E₃ = 0 + 1 = 1
E₄ = (E₂ + 1) (or) (E₃ + 1) = (4 + 1) (or) (1 + 1) = 5 (or) 2
[whichever is maximum we must select forward pass]
∴ E₄ = 5
E₅ = 1 + 6 = 7
E₆ = 7 + 4 = 11
E₇ = 8 + 7 = 15
E₈ = (E₇ + 2) (or) (E₆ + 1)
= (15 + 2) or (11 + 1)
= 17 or 12 [whichever is maximum]
∴ E₈ = 17
E₉ = 5 + 5 = 10
E₁₀ = (E₉ + 7) (or) (E₈ + 5)
= (10 + 7) (or) (17 + 5)
= 17 (or) 22 [Which is maximum]
E₁₀ = 22
Backward pass:
L₁₀ = 22
L₉ = 22 – 7 = 15
L₈ = 22 – 5 = 17
L₇ = 17 – 2 = 15
L₆ = 17 – 1 = 16
L₅ = (16 – 4) (or) (15 – 8) [whichever is minimum]
L₅ = 7
L₄ = 15 – 5 = 10
L₃ = (10 – 1) (or) (7 – 6) [whichever is minimum]
L₃ = 1
L₂ = 10 – 1 = 9
L₁ = 0
We can also find the critical path by this method, which also helps us to counter check the solution obtained by the table method.

So critical path is 1-3-5-7-8-10 as it takes 22 units to complete the project.

Question 7.
Draw the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.

Solution:

Forward pass:
E₁ = 0
E₂ = 0 + 6 = 6
E₃ = 0 + 5 = 5
E₄ = 6 + 10 = 16
E₅ = (E₄ + 6) (or) (E₃ + 4)
E₅ = (16 + 6) (or) (5 + 4) [whichever is maximum]
E₅ = 22
E₆ = (E₅ + 9)(or) (E₄ + 2)
E₆ = (22 + 9) (or) (4 + 2) [whichever is maximum]
E₆ = 31
Backward pass:
L₆ = 31
L₅ = 31 – 9 = 22
L₄ = 22 – 6 (or) 31 – 2 [whichever is minimum]
L₄ = 16
L₃ = 22 – 4 = 18
L₂ = 16 – 10 = 6
L₁ = 6 – 6 = 0


∴ EFT and LFT are the same on 1-2, 2-4, 4-5, 5-6, the vertical path is 1-2-4-5-6 and duration is 31 days to complete.

Question 8.
The following table gives the activities of a project and their duration in days.

Construct the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the critical path of the project and duration to complete the project.
Solution:

Forward pass:
E₁ = 0
E₂ = 0 + 5 = 5
E₃ = (0 + 8) (or) (5 + 6) [whichever is maximum]
E₃ = 11
E₄ = (11 + 5) (or) (5 + 7) [whichever is maximum]
E₄ = 16
E₅ = (11 + 4) (or) (16 + 8) [whichever is maximum]
E₅ = 24
Backward pass:
L₅ = 24
L₄ = 24 – 8 = 16
L₃ = (24 – 4) (or) (16 – 5) [whichever is minimum]
L₃ = 11
L₂ = (11 – 6) (or) (16 – 7) [whichever is minimum]
L₂ = 5
L₁ = (5 – 5) (or) (11 – 8) = 0 [whichever is minimum]


EFT and LFT are the same on 1-2, 2-3, 3-4, and 4-5
So critical path is 1-2-3-4-5 and the time taken is 24 days.

Question 9.
A project has the following time schedule

Construct the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the critical path of the project and duration to complete the project.
Solution:

Forward pass:
E₁ = 0
E₂ = 0 + 7 = 7
E₃ = 7 + 14 = 21
E₄ = 7 + 5 = 12
E₅ = (21 + 11) (or) (2 + 7) = 32 [whichever is maximum]
E₆ = 0 + 6 = 6
E₇ = 6 + 11 = 17
E₈ = 32 + 4 = 36
Backward pass:
L₈ = 36
L₇ = 36 – 18 = 18
L₆ = 18 – 11 = 7
L₅ = 35 – 4 = 31
L₄ = 32 – 7 = 25
L₃ = 32 – 11 = 21
L₂ = (21 – 14) (or) (25 – 5) [whichever is minimum]
L₂ = 7
L₁ = 7 – 7 = 0

EFT and LFT are same is 1-2, 2-3, 3-5, 5-8.
Hence the critical path is 1-2-3-5-8 and the time to complete is 36 days.

Question 10.
The following table uses the activities in construction projects and relevant information.

Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity, and find the critical path. Compute the project duration.
Solution:

Forward pass:
E₁ = 0
E₂ = 0 + 22 = 22
E₃ = (0 + 27) (or) (22 + 12) = 34 [Maximum of both]
E₄ = (22 + 14) (or) (34 + 16) = 40
E₅ = 40 + 12 = 52
Backward pass:
L₅ = 32
L₄ = 52 – 12 = 40
L₃ = 40 – 6 = 34
L₂ = (40 – 14) (or) (34 – 12) = 22 [Minimum of both]
L₁ = 22 – 22 = 0

EFT and LFT are the same for 1-2, 2-3, 3-4, and 4-5.
So critical path is 1-2-3-4-5 time to complete is 52 days.

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 10 Operations Research Ex 10.1

Samacheer Kalvi 11th Business Maths Operations Research Ex 10.1 Text Book Back Questions and Answers

Question 1.
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹5 and ₹3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
Solution:
(i) Variables: Let x₁ and x₂ denotes the number of pens in type A and type B.

(ii) Objective function:
Profit on x₁ pens in type A is = 5x₁
Profit on x₂ pens in type B is = 3x₂
Total profit = 5x₁ + 3x₂
Let Z = 5x₁ + 3x₂, which is the objective function.
Since the B total profit is to be maximized, we have to maximize Z = 5x₁ + 3x₂

(iii) Constraints:
Raw materials required for each pen A is twice as that of pen B.
i.e., for pen A raw material required is 2x₁ and for B is x₂.
Raw material is sufficient only for 1000 pens per day
∴ 2x₁ + x₂ ≤ 1000
Pen A requires 400 clips per day
∴ x₁ ≤ 400
Pen B requires 700 clips per day
∴ x₂ ≤ 700

(iv) Non-negative restriction:
Since the number of pens is non-negative, we have x₁ > 0, x₂ > 0.
Thus, the mathematical formulation of the LPP is
Maximize Z = 5x₁ + 3x₂
Subj ect to the constrains
2x₁ + x₂ ≤ 1000, x₁ ≤ 400, x₂ ≤ 700, x₁, x₂ ≥ 0

Question 2.
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.

Formulate this problem as a linear programming problem to maximize the profit.
Solution:
(i) Variables: Let x₁ and x₂ denote the two types products A and B respectively.

(ii) Objective function:
Profit on x₁ units of type A product = 30x₁
Profit on x₂ units of type B product = 40x₂
Total profit = 30x₁ + 40x₂
Let Z = 30x₁ + 40x₂, which is the objective function.
Since the profit is to be maximized, we have to maximize Z = 30x₁ + 40x₂

(iii) Constraints:
60x₁ + 120x₂ ≤ 12,000
8x₁ + 5x₂ ≤ 600
3x₁ + 4x₂ ≤ 500

(iv) Non-negative constraints:
Since the number of products on type A and type B are non-negative, we have x₁, x₂ ≥ 0
Thus, the mathematical formulation of the LPP is
Maximize Z = 30x₁ + 40x₂
Subject to the constraints,
60x₁ + 120x₂ ≤ 12,000
8x₁ + 5x₂ ≤ 600
3x₁ + 4x₂ ≤ 500
x₁, x₂ ≥ 0

Question 3.
A company manufactures two models of voltage stabilizers viz., ordinary and autocut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at company’s own works. The assembly and testing time required for the two models are 0.8 hour each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
Solution:
(i) Variables : Let x₁ and x₂ denote the number of ordinary and auto-cut voltage stabilized.

(ii) Objective function:
Profit on x₁ units of ordinary stabilizers = 100x₁
Profit on x₂ units of auto-cut stabilized = 150x₂
Total profit = 100x₁ + 150x₂
Let Z = 100x₁ + 150x₂, which is the objective function.
Since the profit is to be maximized. We have to
Maximize, Z = 100x₁ + 15x₂

(iii) Constraints: The assembling and testing time required for x₁ units of ordinary stabilizers = 0.8x₁ and for x₂ units of auto-cut stabilizers = 1.2x₂
Since the manufacturing capacity is 720 hours per week. We get 0.8x₁ + 1.2x₂ ≤ 720
Maximum weekly sale of ordinary stabilizer is 600
i.e., x₁ ≤ 600
Maximum weekly sales of auto-cut stabilizer is 400
i.e., x₂ ≤ 400

(iv) Non-negative restrictions:
Since the number of both the types of stabilizer is non-negative, we get x₁, x₂ ≥ 0.
Thus, the mathematical formulation of the LPP is,
Maximize Z = 100x₂ + 150x₂
Subject to the constraints
0.8x₁ + 1.2x₂ ≤ 720, x₁ ≤ 600, x₂ ≤ 400, x₁, x₂ ≥ 0

Question 4.
Solve the following linear programming problems by graphical method.
(i) Maximize Z = 6x₁ + 8x₂ subject to constraints 30x₁ + 20x₂ ≤ 300; 5x₁ + 10x₂ ≤ 110; and x₁, x₂ ≥ 0.
(ii) Maximize Z = 22x₁ + 18x₂ subject to constraints 960x₁ + 640x₂ ≤ 15360; x₁ + x₂ ≤ 20 and x₁, x₂ ≥ 0.
(iii) Minimize Z = 3x₁ + 2x₂ subject to the constraints 5x₁ + x₂ ≥ 10; x₁ + x₂ > 6; x₁+ 4x₂ ≥ 12 and x₁, x₂ ≥ 0.
(iv) Maximize Z = 40x₁ + 50x₂ subject to constraints 3x₁ + x₂ ≤ 9; x₁ + 2x₂ ≤ 8 and x₁, x₂ ≥ 0.
(v) Maximize Z = 20x₁ + 30x₂ subject to constraints 3x₁ + 3x₂ ≤ 36; 5x₁ + 2x₂ ≤ 50; 2x₁ + 6x₂ ≤ 60 and x₁, x₂ ≥ 0.
(vi) Minimize Z = 20x₁ + 40x₂ subject to the constraints 36x₁ + 6x₂ ≥ 108; 3x₁ + 12x₂ ≥ 36; 20x₁ + 10x₂ ≥ 100 and x₁, x₂ ≥ 0.
Solution:
(i) Given that 30x₁ + 20x₂ ≤ 300
Let 30x₁ + 20x₂ = 300

Therefore
3x₁ + 2x₂ = 30

Also given that 5x₁ + 10x₂ ≤ 110
Let 5x₁ + 10x₂ = 110
x₁ + 2x₂ = 22

To get point of intersection, (i.e., the to get eo-ordinates of B)
3x₁ + 2x₂ = 30 …….(1)
x₁ + 2x₂ = 22 ……..(2)
(1) – (2) ⇒ 2x₁ = 8
x₁ = 4
x₁ = 4 substitute in (1),
x₁ + 2x₂ = 22
4 + 2x₂ = 22
2x₂ = 18
x₂ = 9
i.e., B is (4, 9)
The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the points are O(0, 0), A(10, 0), B(4, 9), C(0, 11).

The maximum value of Z occurs at B.
∴ The optimal solution is x₁ = 4, x₂ = 9 and Z_max = 96

(ii) Given that 960x₁ + 640x₂ ≤ 15360
Let 960x₁ + 640x₂ = 15360
3x₁ + 2x₂ = 48

Also given that x₁ + x₂ ≤ 20
Let x₁ + x₂ = 20

To get point of intersection
3x₁ + 2x₂= 48 …..(1)
x₁ + x₂ = 20 ……(2)
(2) × -2 ⇒ -2x₁ – 2x₂ = -40 …..(3)
(1) + (3) ⇒ x₁ = 8
x₁ = 8 substitute in (2),
8 + x₂ = 20
x₂ = 12

The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the comer points are O(0, 0), A(16, 0), B(8,12) and C(0, 16).

The maximum value of Z occurs at B(8, 12).
∴ The optimal solution is x₁ = 8, x₂ = 12 and Z_max = 392

(iii) Given that 5x₁ + x₂ ≥ 10
Let 5x₁ + x₂ = 10

Also given that x₁ + x₂ ≥ 6
Let x₁ + x₂ = 6

Also given that x₁ + 4x₂ ≥ 12
Let x₁ + 4x₂ = 12

To get C
5x₁ + x₂ = 10 ……..(1)
x₁ + x₂ = 6 ………(2)
(1) – (2) ⇒ 4x₁ = 4
⇒ x₁ = 1
x = 1 substitute in (2)
⇒ x₁ + x₂ = 6
⇒ 1 + x₂ = 6
⇒ x₂ = 5
∴ C is (1, 5)
To get B
x₁ + x₂ = 6
x₁ + 4x₂ = 12
(1) – (2) ⇒ -3x₂ = -6
x₂ = 2
x₂ = 2 substitute in (1), x₁ = 4
∴ B is (4, 2)

The feasible region satisfying all the conditions is ABCD.
The co-ordinates of the comer points are A(12, 0), B(4, 2), C(1, 5) and D(0, 10).

The minimum value of Z occours at C(1, 5).
∴ The optimal solution is x₁ = 1, x₂ = 5 and Z_min = 13

(iv) Given that 3x₁ + x₂ ≤ 9
Let 3x₁ + x₂ = 9

Also given that x₁ + 2x₂ ≤ 8
Let x₁ + 2x₂ = 8

3x₁ + x₂ = 9 ………(1)
x₁ + 2x₂ = 8 ……..(2)
(1) × 2 ⇒ 6x₁ + 2x₂ = 18 ……..(3)
(2) + (3) ⇒ -5x₁ = -10
x₁ = 2
x₁ = 2 substitute in (1)
3(2) + x₂ = 9
x₂ = 3
The feasible region satisfying all the conditions is OABC.
The co-ordinates of the corner points are O(0, 0), A(3, 0), B(2, 3), C(0, 4)

The maximum value of Z occurs at (2, 3).
∴ The optimal solution is x₁ = 2, x₂ = 3 and Z_max = 230

(v) Given that 3x₁ + 3x₂ ≤ 36
Let 3x₁ + 3x₂ = 36

Also given that 5x₁ + 2x₂ ≤ 50
Let 5x₁ + 2x₂ = 50

x₁ + x₂ = 12 ……(1)
5x₁ + 2x₂ = 50 ……….(2)
(1) × 2 ⇒ 2x₁ + 2x₂ = 24 ………(3)
(2) – (3) ⇒ 3x₁ = 26
x₁ = \(\frac{26}{3}\) = 8.66
put x₁ = \(\frac{26}{3}\) substitute in (1)
x₁ + x₂ = 12
x₂ = 12 – x₁
x₂ = 26 – \(\frac{26}{3}\) = \(\frac{10}{3}\) = 3.33
Also given that 2x₁ + 6x₂ ≤ 60
Let 2x₁ + 6x₂ = 60
x₁ + 3x₂ = 30

x₁ + x₂ = 12 …….(1)
x₁ + 3x₂ = 30 …….(2)
(1) – (2) ⇒ -2x₂ = -18
x₂ = 9
x₂ = 9 substitute in (1) ⇒ x₁ = 3

The feasible region satisfying all the given conditions is OABCD.
The co-ordinates of the comer points are O(0, 0), A(10, 0), B(\(\frac{26}{3}, \frac{10}{3}\)), and C = (3, 9) and D (0, 10)

The maximum value of Z occurs at C(3, 9)
∴ The optimal solution is x₁ = 3, x₂ = 9 and Z_max = 330

(vi) Given that 36x₁ + 6x₂ ≥ 108
Let 36x₁ + 6x₂ = 108
6x₁ + x₂ = 18

Also given that 3x₁ + 12x₂ ≥ 36
Let 3x₁ + 12x₂ = 36
x₁ + 4x₂ = 12

Also given that 20x₁ + 10x₂ ≥ 100
Let 20x₁ + 10x₂ = 100
2x₁ + x₂ = 10

The feasible region satisfying all the conditions is ABCD.
The co-ordinates of the comer points are A(12, 0), B(4, 2), C(2, 6) and D(0, 18).

The minimum value of Z occurs at B(4, 2)
∴ The optimal solution is x₁ = 4, x₂ = 2 and Z_min = 160

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 9 Correlation and Regression Analysis Ex 9.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 9 Correlation and Regression Analysis Ex 9.3

Samacheer Kalvi 11th Business Maths Correlation and Regression Analysis Ex 9.3 Text Book Back Questions and Answers

Choose the correct answer.

Question 1.
An example of a positive correlation is:
(a) Income and expenditure
(b) Price and demand
(c) Repayment period and EMI
(d) Weight and Income
Answer:
(a) Income and expenditure

Question 2.
If the values of two variables move in the same direction then the correlation is said to be:
(a) Negative
(b) Positive
(c) Perfect positive
(d) No correlation
Answer:
(b) Positive

Question 3.
If the values of two variables move in the opposite direction then the correlation is said to be:
(a) Negative
(b) Positive
(c) Perfect positive
(d) No correlation
Answer:
(a) Negative

Question 4.
Correlation co-efficient lies between:
(a) 0 to ∞
(b) -1 to +1
(c) -1 to 0
(d) -1 to ∞
Answer:
(b) -1 to +1

Question 5.
If r(X, Y) = 0 the variables X and Y are said to be:
(a) Positive correlation
(b) Negative correlation
(c) No correlation
(d) Perfect positive correlation
Answer:
(c) No correlation

Question 6.
The correlation coefficient from the following data N = 25, ΣX = 125, ΣY = 100, ΣX² = 650, ΣY²= 436, ΣXY = 520:
(a) 0.667
(b) -0.006
(c) -0.667
(d) 0.70
Answer:
(a) 0.667
Hint:

Question 7.
From the following data, N = 11, ΣX = 117, ΣY = 260, ΣX² = 1313, ΣY² = 6580, ΣXY = 2827. the correlation coefficient is:
(a) 0.3566
(b) -0.3566
(c) 0
(d) 0.4566
Answer:
(a) 0.3566
Hint:

Question 8.
The correlation coefficient is:

Answer:
(b) r(X, Y) = \(\frac{cov(x, y)}{\sigma_{x} \sigma_{y}}\)

Question 9.
The variable whose value is influenced or is to be predicted is called:
(a) dependent variable
(b) independent variable
(c) regressor
(d) explanatory variable
Answer:
(a) dependent variable

Question 10.
The variable which influences the values or is used for prediction is called:
(a) Dependent variable
(b) Independent variable
(c) Explained variable
(d) Regressed
Answer:
(b) Independent variable

Question 11.
The correlation coefficient:

Answer:
(a) \(r=\pm \sqrt{b_{x y} \times b_{y x}}\)

Question 12.
The regression coefficient of X on Y:

Answer:
(a) \(b_{x y}=\frac{\mathrm{N} \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{\mathrm{N} \Sigma d y^{2}-(\Sigma d y)^{2}}\)

Question 13.
The regression coefficient of Y on X:

Answer:
(c) \(b_{y x}=\frac{\mathrm{N\Sigma} d x d y-(\Sigma d x)(\Sigma d y)}{\mathrm{N} \Sigma d x^{2}-(\Sigma d x)^{2}}\)

Question 14.
When one regression coefficient is negative, the other would be:
(a) Negative
(b) Positive
(c) Zero
(d) None of these
Answer:
(a) Negative

Question 15.
If X and Y are two variates, there can be at most:
(a) one regression line
(b) two regression lines
(c) three regression lines
(d) more regression lines
Answer:
(b) two regression lines

Question 16.
The lines of regression of X on Y estimates:
(a) X for a given value of Y
(b) Y for a given value of X
(c) X from Y and Y from X
(d) none of these
Answer:
(a) X for a given value of Y

Question 17.
Scatter diagram of the variate values (X, Y) give the idea about:
(a) functional relationship
(b) regression model
(c) distribution of errors
(d) no relation
Answer:
(a) functional relationship

Question 18.
If regression co-efficient of Y on X is 2, then the regression co-efficient of X on Y is:
(a) ≤ \(\frac{1}{2}\)
(b) 2
(c) > \(\frac{1}{2}\)
(d) 1
Answer:
(a) ≤ \(\frac{1}{2}\)

Question 19.
If two variables move in a decreasing direction then the correlation is:
(a) positive
(b) negative
(c) perfect negative
(d) no correlation
Answer:
(a) positive

Question 20.
The person suggested a mathematical method for measuring the magnitude of the linear relationship between two variables say X and Y is:
(a) Karl Pearson
(b) Spearman
(c) Croxton and Cowden
(d) Ya Lun Chou
Answer:
(a) Karl Pearson

Question 21.
The lines of regression intersect at the point:
(a) (X, Y)
(b) \((\overline{\mathrm{X}}, \overline{\mathrm{Y}})\)
(c) (0, 0)
(d) (σ_x, σ_y)
Answer:
(b) \((\overline{\mathrm{X}}, \overline{\mathrm{Y}})\)

Question 22.
The term regression was introduced by:
(a) R.A Fisher
(b) Sir Francis Galton
(c) Karl Pearson
(d) Croxton and Cowden
Answer:
(b) Sir Francis Galton

Question 23.
If r = -1, then correlation between the variables:
(a) perfect positive
(b) perfect negative
(c) negative
(d) no correlation
Answer:
(b) perfect negative

Question 24.
The coefficient of correlation describes:
(a) the magnitude and direction
(b) only magnitude
(c) only direction
(d) no magnitude and no direction
Answer:
(a) the magnitude and direction

Question 25.
If Cov(x, y) = -16.5, \(\sigma_{x}^{2}\) = 2.89, \(\sigma_{y}^{2}\) = 100. Find correlation coeffient.
(a) -0.12
(b) 0.001
(c) -1
(d) -0.97
Answer:
(d) -0.97

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 7 Financial Mathematics Ex 7.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 7 Financial Mathematics Ex 7.2

Samacheer Kalvi 11th Business Maths Financial Mathematics Ex 7.2 Text Book Back Questions and Answers

Question 1.
Find the market value of 62 shares available at ₹ 132 having the par value of ₹ 100.
Solution:
Market value = ₹ Number of shares × Market value of a share
= ₹ 132 × 62
= ₹ 8,184

Question 2.
How much will be required to buy 125 of ₹ 25 shares at a discount of ₹ 7.
Solution:
Face value of a share = ₹ 25
Market value of a share = ₹ 25 – 7 = ₹ 18
Amount of money required to buy 125 shares = Number of shares × Market value of a share
= ₹ 125 × 18
= ₹ 2,250

Question 3.
If the dividend received from 9% of ₹ 20 shares is ₹ 1,620, find the number of shares.
Solution:
Income = Number of shares × Face value of a share × Rate of dividend
1620 = Number of shares × 20 × \(\frac{9}{100}\)
Number of shares = \(\frac{1620 \times 100}{20 \times 9}\) = 900 shares

Question 4.
Mohan invested ₹ 29,040 in 15% of ₹ 100 shares of a company quoted at a premium of 20%. Calculate
(i) the number of shares bought by Mohan
(ii) his annual income from shares
(iii) the percentage return on his investment
Solution:
Investment = ₹ 29,040
Rate of dividend = 15%
Number of shares = 100
Premium = 20%
(i) Number of shares

(ii) Annual income from shares = (Number of shares) × (Face value of a share) × (Rate of dividend)
= 242 × 100 × \(\frac{15}{100}\)
= ₹ 3630

(iii) The percentage return on his investment

Question 5.
A man buys 400 of ₹ 10 shares at a premium of ₹ 2.50 on each share. If the rate of dividend is 12% find
(i) his investment
(ii) annual dividend received by him
(iii) rate of interest received by him on his money
Solution:
(i) Given Number of shares = 400
Face value of a share ₹ 10 market values of a share = 10 + 2.50 = ₹ 12.50
Investment = Number of shares × Market value of a share = ₹ 400 × 12.50 = ₹ 5000

(ii) Annual dividend = Number of shares × Face value × Rate of dividend
= 400 × 10 × \(\frac{12}{100}\)
= ₹ 480

(iii) Rate of dividend = \(\frac{\text { Dividend }}{\text { Investment }}\) × 100
= \(\frac{480}{5000}\) × 100
= \(\frac{48}{5}\)
= 9.6%

Question 6.
Sundar bought 4,500 of ₹ 10 shares, paying 2% per annum. He sold them when the price rose to ₹ 23 and invested the proceeds in ₹ 25 shares paying 10% per annum at ₹ 18. Find the change in his income.
Solution:
Number of shares = \(\frac{4500}{10}\) = 450
Income from 2% stock = Number of shares × face value × Rate of dividend
= 450 × 10 × \(\frac{2}{100}\)
= ₹ 90
Selling price of450 shares = 450 × 23 = ₹ 10,350
Number of shares bought in 10% stock = \(\frac{\text { Selling price of } 450 \text { shares at } ₹ 23}{\text { Market value }}\)
= \(\frac{10350}{18}\)
= ₹ 575
Income, from 10% stock = No of shares × face value × Rate of dividend
= 575 × 25 × \(\frac{10}{100}\)
= 575 × \(\frac{10}{4}\)
= ₹ 1437.5
= ₹ 1437.50
Charge in his income = ₹ 1437.50 – ₹ 90 = ₹ 1347.50

Question 7.
A man invests ₹ 13,500 partly in 6% of ₹ 100 shares at ₹ 140 and partly in 5% of ₹ 100 shares at ₹ 125. If his total income is ₹ 560, how much has he invested in each?
Solution:
Let the amount invested in 6% of ₹ 100 shares at ₹ 140 be x.
Then the amount invested in 5% of ₹ 100 shares at ₹ 125 is ₹ 13500 – x.
Income from 6% shares = Number of shares × Face value of a share × Rate of dividend
= \(\frac{x}{140} \times 100 \times \frac{6}{100}\)
= \(\frac{3 x}{70}\)
Income from 5% shares = Number of shares × Face value of a share × Rate of dividend
= \(\frac{13500-x}{125} \times 100 \times \frac{5}{100}\)
= \(\frac{13500-x}{25}\)
Given that the total income = ₹ 560

x + 13500 × 14 = 560 × 350
x = 196000 – 189000 = 7000
Amount invested at 6% stock = ₹ 7,000
Amount invested at 5% stock = ₹ 13500 – ₹ 7000 = ₹ 6500

Question 8.
Babu sold some ₹ 100 Shares at a 10% discount and invested his sales proceeds in 15% of ₹ 50 shares at ₹ 33. Had he sold his shares at a 10% premium instead of a 10% discount, he would have earned ₹ 450 more. Find the number of shares sold by him.
Solution:
Let the number of shares sold by Babu be x.
The face value of a share is ₹ 100.
He sold a 10% discount; the selling price of one share ₹ 90.
The selling price of x shares = ₹ 90x
He bought a share of face value ₹ 50 and the number of shares 33.
∴ Number of shares bought for the amount ₹ 90x i.e., \(\frac{90 x}{33}\)
∴ Face value of 50 shares = Cost of one share × Number of share
= 50 × \(\frac{90 x}{33}\)
The dividend is 15%.
∴ Income = \(\frac{15}{100}\) × Face value of 50 shares
= \(\frac{15}{100} \times 50 \times \frac{90 x}{33}\)
= \(\frac{225 x}{11}\)
Suppose he sold his shares at 10% premium instead of 10% discount, the market value of one share is ₹ 110.
Selling price of x shares = 110 × x = 110x
Number of shares bought for ₹ 33 = \(\frac{110 x}{33}\)
Face value of 50 shares = \(\frac{110 x}{33}\) × 50
Income = \(\frac{15}{100} \times \frac{110 x}{33}\) × 50 = 25x
Change Income = ₹ 450

x = \(\frac{450}{50}\) × 11 = 9 × 11 = 99 shares

Question 9.
Which is better investment? 7% of ₹ 100 shares at ₹ 120 (or) 8% of ₹ 100 shares at ₹ 135.
Solution:
Let the investment in each case be ₹ (120 × 135)
Case (i): Income from 7% of ₹ 100 shares at ₹ 120 = \(\frac{7}{120}\) × 120 × 135
= 7 × 135
= ₹ 945

Case (ii): Income from 8% of ₹ 100 shares at ₹ 135 = \(\frac{8}{135}\) × (120 × 135)
= 8 × 120
= ₹ 960
∴ 8% of 100 shares at ₹ 135 is better investment.

Question 10.
Which is better investment? 20% stock at 140 (or) 10% stock at 70.
Solution:
Let the investment in case be ₹ 140 × 70
Income from 20% stock at ₹ 140 is = \(\frac{20}{140}\) × 140 × 70
= 20 × 70
= ₹ 1400
Income from 10% stock at 70 = \(\frac{10}{70}\) × 140 × 70 = ₹ 1400
For the same investtnent both stocks fetch the same income. Therefore they are equivalent shares.

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 7 Financial Mathematics Ex 7.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 7 Financial Mathematics Ex 7.1

Samacheer Kalvi 11th Business Maths Financial Mathematics Ex 7.1 Text Book Back Questions and Answers

Question 1.
Find the amount of an ordinary annuity of ₹ 3,200 per annum for 12 years at the rate of interest of 10% per year, [(1.1)¹² = 3.1384]
Solution:
Here a = 3,200, n = 12, and i = \(\frac{10}{100}\) = 0.1
A = \(\frac{a}{i}\) [(1 + i)ⁿ – 1]
= \(\frac{3200}{0.1}\) [(1 + 0.1)¹² – 1]
= 32000 [(1.1)¹² – 1]
= 32000 [3.1384 – 1] [∵ (1.1)¹² = 3.1384]
= 32000 [2.1384]
= ₹ 68,428.8

Question 2.
If the payment of ₹ 2,000 is made at the end of every quarter for 10 years at the rate of 8% per year, then find the amount of annuity. [(1.02)⁴⁰ = 2.2080]
Solution:
Here a = 2,000, n = 10 years, and \(\frac{i}{k}=\frac{\frac{8}{100}}{4}=\frac{2}{100}=0.02\)

= 100000 [2.2080 – 1] [∵ (1.02)⁴⁰ = 2.2080]
= 100000 [1.2080]
= ₹ 1,20,800

Question 3.
Find the amount of an ordinary annuity of 12 monthly payments of ₹ 1,500 that earns interest at 12% per annum compounded monthly. [(1.01)¹² = 1.1262]
Solution:
Here a = 1,500, n = 1 year, and i = \(\frac{12}{100}\)

= 150000 [(1.01)¹² – 1]
= 150000 [1.1262 – 1] (∵ (1.01)¹² = 1.1262)
= 150000 [0.1262]
= ₹ 18,930

Question 4.
A bank pays 8% per annum interest compounded quarterly. Find equal deposits to be made at the end of each quarter for 10 years to have ₹ 30,200? [(1.02)⁴⁰ = 2.2080]
Solution:
Here A = ₹ 30200, i = \(\frac{8}{100}\)

Question 5.
A person deposits ₹ 2,000 from his salary towards his contributory pension scheme. The same amount is credited by his employer also. If an 8% rate of compound interest is paid, then find the maturity amount at end of 20 years of service. [(1.0067)²⁴⁰ = 4.966]
Solution:
A person deposit ₹ 2,000.
The employer also credited the same amount.
a = ₹ 2,000 + ₹ 2,000 = ₹ 4,000

Note:
If (1.0067) = 4.966 (Original value)
Then A = 600000 (4.966 – 1)
= 600000(3.966)
= ₹ 23,79,600

Question 6.
Find the present value of ₹ 2,000 per annum for 14 years at the rate of interest of 10% per annum. [(1.04)^-14 = 0.6252]
Solution:
Here a = 2000, n = 14, and i = \(\frac{10}{100}\) = 0.1
\(P=\frac{a}{i}\left[1-\frac{1}{(1+i)^{n}}\right]\)
= \(\frac{2000}{0.1}\left[1-\frac{1}{(1+0.1)^{14}}\right]\)
= \(\frac{2000}{0.1}\left[1-(1.1)^{-14}\right]\)
= 20000 [1 – 0.2632]
= 20000 × 0.73678
= ₹ 14,735.60

Question 7.
Find the present value of an annuity of ₹ 900 payable at the end of 6 months for 6 years. The money compounded at 8% per annum. [(1.04)^-12 = 0.6252]
Solution:

Question 8.
Find the amount at the end of 12 years of an annuity of ₹ 5,000 payable at the beginning of each year, if the money is compounded at 10% per annum.
Solution:
Here a = 5000, i = 10% = \(\frac{10}{100}\) = 0.1, n = 12
Amount A = (1 + i) \(\frac{a}{i}\) [(1 + i)ⁿ – 1]
= (1 + 0.1) \(\frac{5000}{\frac{10}{100}}\) [(1 + 0.1)¹² – 1]
= (1.1) 50000 [(1.1)¹² – 1]
= 55000 [3.1384 – 1]
= 55000 [2.1384]
= ₹ 1,17,612

Question 9.
What is the present value of an annuity due of ₹ 1,500 for 16 years at 8% per annum? [(1.08)¹⁵ = 3.172]
Solution:
Present value of annuity due, \(\mathrm{P}=\frac{a(1+i)}{i}\left[1-\frac{1}{(1+i)^{n}}\right]\)
Here a = 1500, n = 16, i = \(\frac{8}{100}\) = 0.08

= 18750[1.08 – \(\frac{1}{3.1721}\)] [∵ (1.08)¹⁵ = 3.1721]
= 18750[1.08 – 0.31524]
= 18750[0.7648]
= ₹ 14340

Question 10.
What is the amount of perpetual annuity of ₹ 50 at 5% compound interest per year?
Solution:
\(P=\frac{a}{i}=\frac{50}{\left(\frac{5}{100}\right)}=\frac{50 \times 100}{5}=₹ 1,000\)

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 9 Correlation and Regression Analysis Ex 9.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 9 Correlation and Regression Analysis Ex 9.2

Samacheer Kalvi 11th Business Maths Correlation and Regression Analysis Ex 9.2 Text Book Back Questions and Answers

Question 1.
From the data given below:

Find
(a) The two regression equations
(b) The coefficient of correlation between marks in Economics and statistics
(c) The most likely marks in Statistics when the marks in Economics is 30.
Solution:

(a) Regression equation of X on Y.

Regression equation of Y on X.

(b) Coefficient of correlation \(r=\pm \sqrt{b_{x y} \times b_{y x}}\)
= \(\sqrt{(-0.234)(-0.664)}\)
= -0.394
(c) When X = 30, Y = ?
Y = -0.664(30) + 59.248
= -19.92 + 59.248
= 39.328.

Question 2.
The heights (in cm.) of a group of fathers and sons are given below.

Find the lines of regression and estimate the height of son when the height of the father is 164 cm.
Solution:

\(\overline{\mathrm{Y}}=\frac{1690}{10}=169\)

Regression equation of X on Y


Regression equation of Y on X
\(\mathrm{Y}-\overline{\mathrm{Y}}=b_{\mathrm{yx}}(\mathrm{X}-\overline{\mathrm{X}})\)
Y – 169 = 0.610 (X – 168.6)
Y – 169 = 0.610X – 102.846
Y = 0.610X – 102.846 + 169
Y = 0.160X + 66.154 ………(1)
To get son’s height (Y) when the father height is X = 164 cm.
Put X = 164 cm in equation (1) we get
Son’s height = 0.610 × 164 + 66.154
= 100.04 + 66.154 cm
= 169.19 cm.

Question 3.
The following data give the height in inches (X) and the weight in lb. (Y) of a random sample of 10 students from a large group of students of age 17 years:

Estimate weight of the student of a height 69 inches.
Solution:

\(\overline{\mathrm{Y}}=\frac{1169}{10}=116.9\)

Regression equation of Y on X
\(Y-\bar{Y}=b_{y x}(X-\bar{X})\)
Y – 117 = 2.3479 (X – 65.2)
Y – 117 = 2.3479X – (2.3479)(65.2)
Y = 2.3479X – 153.08308 + 117
Y = 2.3479 – 36.08308
When the height X = 69 inches
Weight, Y = 2.3479(69) – 36.08308
= 162.0051 – 36.08308
= 125.92202
= 125.92 lb

Question 4.
Obtain the two regression lines from the following data N = 20, ΣX = 80, ΣY = 40, ΣX² = 1680, ΣY² = 320 and ΣXY = 480.
Solution:
ΣX = 80, ΣY = 40, ΣX² = 1680, ΣY² = 320, ΣXY = 480, N = 20

Regression line of Y on X

Regression line of X on Y
\(\mathbf{X}-\overline{\mathbf{X}}=b_{x y}(\mathbf{Y}-\overline{\mathbf{Y}})\)
X – 4 = 1.33(Y – 2)
X = 1.33Y – 2.66 + 4
X = 1.33Y + 1.34

Question 5.
Given the following data, what will be the possible yield when the rainfall is 29″

The coefficient of correlation between rainfall and production is 0.8.
Solution:
\(\overline{\mathrm{X}}\) = 25, σ_x = 3, \(\overline{\mathrm{Y}}\) = 40, σ_y = 6, r = 0.8

To find the yield when the rainfall is 29″ is,
Put X = 29 in the above equation we get yield,
Y = 1.6 × 29 = 46.4 units/acre

Question 6.
The following data relate to advertisement expenditure (in lakh of rupees) and their corresponding sales (in crores of rupees)

Estimate the sales corresponding to advertising expenditure of ₹ 30 lakh.
Solution:

N = 7, ΣX = 338, ΣY = 361, ΣX² = 17094, ΣY² = 19773, ΣXY = 18160.

Regression equation of Y on X
\(Y-\bar{Y}=b_{y x}(X-\bar{X})\)
Y – 51.57 = 0.942(X – 48.29)
Y – 51.57 = 0.942X – 0.942 × 48.29
Y – 51.57 = 0.942X – 45.48918
Y = 0.942X + 51.57 – 48.29
Y = 0.942X + 6.081
To find the sales, when the advertising is X = ₹ 30 lakh in the above equation we get,
Y = 0.942(30) + 6.081
= 28.26 + 6.081
= 34.341
= ₹ 34.34 crores

Question 7.
You are given the following data:

If the Correlation coefficient between X and Y is 0.66, then find
(i) the two regression coefficients,
(ii) the most likely value of Y when X = 10.
Solution:
\(\overline{\mathrm{X}}\) = 36, \(\overline{\mathrm{Y}}\) = 85, σ_x = 11, σ_y = 8, r = 0.66
(i) The two regression coefficients are,

(ii) Regression equation of X on Y:
\(X-\bar{X}=b_{x y}(Y-\bar{Y})\)
X – 36 = 0.91(Y – 85)
X – 36 = 0.91Y – 77.35
X = 0.91Y – 77.35 + 36
X = 0.91Y – 41.35
Regression line of Y on X:
\(Y-\bar{Y}=b_{y x}(X-\bar{X})\)
Y – 85 = 0.48(X – 36)
Y = 0.48X – 17.28 + 85
Y = 0.48X + 67.72
The most likely value of Y when X = 10 is
Y = 0.48(10) + 67.72 = 72.52.

Question 8.
Find the equation of the regression line of Y on X, if the observations (X_i, Y_i) are the following (1, 4) (2, 8) (3, 2) ( 4, 12) ( 5, 10) ( 6, 14) ( 7, 16) ( 8, 6) (9, 18).
Solution:



Regression line of Y on X:
\(Y-\bar{Y}=b_{y x}(X-\bar{X})\)
Y – 10 = 1.33(X – 5)
Y = 1.33X – 6.65 + 10
Y = 1.33X + 3.35

Question 9.
A survey was conducted to study the relationship between expenditure on accommodation (X) and expenditure on Food and Entertainment (Y) and the following results were obtained:

Write down the regression equation and estimate the expenditure on Food and Entertainment, if the expenditure on accommodation is ₹ 200.
Solution:
\(\overline{\mathrm{X}}\) = 178, \(\overline{\mathrm{Y}}\) = 47.8, σ_x = 63.15, σ_y = 22.98, r = 0.43

Regression line of Y on X:
\(\mathrm{Y}-\overline{\mathrm{Y}}=b_{y x}(\mathrm{X}-\overline{\mathrm{X}})\)
Y – 47.8 = 0.1565(X – 178)
Y = 0.1565X – 27.857 + 47.8
Y = 0.1565X + 19.94
When the expenditure on accommodation is ₹ 200 the expenditure on food and entertainments is,
Y = 0.1565X + 19.94
Y = 0.1565(200) + 19.94
= 31.3 + 19.94
= ₹ 51.24.

Question 10.
For 5 observations of pairs of (X, Y) of variables X and Y the following results are obtained.
ΣX = 15, ΣY = 25, ΣX² = 55, ΣY² = 135, ΣXY = 83. Find the equation of the lines of regression and estimate the values of X and Y if Y = 8; X = 12.
Solution:
N = 5, ΣX = 15, ΣY = 25, ΣX² = 55, ΣY² = 135, ΣXY = 83, \(\overline{\mathrm{X}}=\frac{15}{5}\) = 3, \(\overrightarrow{\mathrm{Y}}=\frac{25}{5}\) = 5.

Regression line of Y on X:
\(Y-\bar{Y}=b_{x y}(X-\bar{X})\)
Y – 5 = 0.8(X – 3)
Y = 0.8X – 2.4 + 5
Y = 0.8X + 2.6.
WhenX = 12, Y = 0.8X + 2.6
Y = (0.8)12 + 2.6
= 9.6 + 2.6
= 12.2

Regression line of X on Y:
\(X-\bar{X}=b_{x y}(Y-\bar{Y})\)
X – 3 = 0.8(Y – 5)
X = 0.8Y – 4 + 3
X = 0.8Y – 1
When Y = 8, X = 0.8Y – 1
X = (0.8)8 – 1
= 6.4 – 1
= 5.4

Question 11.
The two regression lines were found to be 4X – 5Y + 33 = 0 and 20X – 9Y – 107 = 0. Find the mean values and coefficient of correlation between X and Y.
Solution:
To get mean values we must solve the given lines.
4X – 5Y = -33 ……(1)
20X – 9Y = 107 …….(2)
(1) × 5 ⇒ 20X – 25Y = -165
20X – 9Y = 107
Subtracting (1) and (2), -16Y = -272
Y = \(\frac{272}{16}\) = 17
i.e., \(\overline{\mathrm{Y}}\) = 17
Using Y = 17 in (1) we get, 4X – 85 = -33
4X = 85 – 33
4X = 52
X = 13
i.e., \(\overline{\mathrm{X}}\) = 13
Mean values are \(\overline{\mathrm{X}}\) = 13, \(\overline{\mathrm{Y}}\) = 17,
Let regression line of Y on X be
4X – 5Y + 33 = 0
5Y = 4X + 33
Y = \(\frac{1}{5}\) (4X + 33)
Y = \(\frac{4}{5} X+\frac{33}{5}\)
Y = 0.8X + 6.6
∴ b_yx = 0.8
Let regression line of X on Y be
20X – 9Y – 107 = 0
20X = 9Y + 107
X = \(\frac{1}{20}\) (9Y + 107)
X = \(\frac{9}{20} Y+\frac{107}{20}\)
X = 0.45Y + 5.35
∴ b_xy = 0.45
Coefficient of correlation between X and Y is
\(r=\pm \sqrt{b_{y x} \times b_{x y}}\)
\(r=\pm \sqrt{0.8 \times 0.45}\)
= ±0.6
= 0.6
Both byx and bxy is positive take positive sign.

Question 12.
The equations of two lines of regression obtained in a correlation analysis are the following 2X = 8 – 3Y and 2Y = 5 – X . Obtain the value of the regression coefficients and correlation coefficient.
Solution:
Let regression line of Y on X be,
2Y = 5 – X
Y = -0.5X + 2.5
b_yx = -0.5
i.e., b_yx= \(-\frac{1}{2}\)
Let regression line of X on Y be
2X = 8 – 3Y
X = -1.5Y + 4
b_xy = -1.5
i.e., b_xy = \(-\frac{3}{2}\)
Correlation coefficient \(r=\pm \sqrt{b_{x y} \times b_{y x}}\)
= \(\pm \sqrt{1.5 \times 0.5}\)
= -0.866
Both b_xy and b_yx is negative so take negative sign.

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 9 Correlation and Regression Analysis Ex 9.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 9 Correlation and Regression Analysis Ex 9.1

Samacheer Kalvi 11th Business Maths Correlation and Regression Analysis Ex 9.1 Text Book Back Questions and Answers

Question 1.
Calculate the correlation co-efficient for the following data:

Solution:

Coefficient of correlation

Question 2.
Find the coefficient of correlation for the following:

Solution:

Question 3.
Calculate the coefficient of correlation for the ages of husbands and their respective wives:

Solution:
Without deviation:

N = 10
Coefficient of correlation

= \(\frac{1783}{45 \times 39.76}\)
= 0.9965
Note: We can do the above problem using deviations taken from arithmetic means of X and Y. i.e., using
r = \(\frac{\Sigma \mathrm{XY}}{\sqrt{\Sigma \mathrm{X}^{2} \Sigma \mathrm{Y}^{2}}}\)

Question 4.
Calculate the coefficient of correlation between X and Y series from the following data:

The summation of product deviations of X and Y series from their respective arithmetic means is 122.
Solution:
N = 15, \(\overline{\mathrm{X}}\) = 25, \(\overline{\mathrm{Y}}\) = 18, x = X – \(\overline{\mathrm{X}}\), y = Y – \(\overline{\mathrm{Y}}\), Σx² = 136, Σy² = 138, Σxy = 122
Correlation coefficient

Question 5.
Calculate the correlation coefficient for the following data:

Solution:

N = 10, ΣX = 310, ΣY = 340, Σx² = 870, Σy² = 720, Σxy = 178

Correlation coefficient

Question 6.
Find the coefficient of correlation for the following:

Solution:

N = 8, ΣX = 600, ΣY = 724, Σdx² = 1172, Σdy² = 3372, Σdxdy = -146
Correlation coefficient

Question 7.
An examination of 11 applicants for an accountant post was taken by a finance company. The marks obtained by the applicants in the reasoning and aptitude tests are given below.

Calculate Spearman’s rank correlation coefficient from the data given above.
Solution:

N = 11, Σd² = 22
Rank correlation

Question 8.
The following are the ranks obtained by 10 students in commerce and accountancy are given below:

To what extent is the knowledge of students in the two subjects related?
Solution:

N = 11, Σd² = 128
Rank correlation

Question 9.
A random sample of recent repair jobs was selected and the estimated cost and actual cost were recorded.

Calculate the value of spearman’s correlation coefficient.
Solution:


N = 8, Σd² = 8
Rank correlation

Question 10.
The rank of 10 students of the same batch in two subjects A and B are given below. Calculate the rank correlation coefficient.

Solution:

N = 10, Σd² = 226
Rank correlation